简介
提供两个文件的 binary diff 的patch 补丁
Patch 的数据结构
- Control Data: 补丁过层指导
- Diff Data: 新旧两个版本文件的差异
- Extra data:在新文件里完全没有的data
基于stream的设计
通过stream来抽象 io 操作,方便在多种环境(实测linux server, android,ios设备都有一致性, server打出来的patch 可以直接在端上merge)
二进制diff算法
Suffix Array Generation 后缀数组
针对于 老文件,进行 利用 qsufsort 进行排序,实际上就是产出一份方便匹配的数据
- 为每个字节值创建桶(0-255)
- 计算每个字节的出现次数并计算桶位置
- 将后缀放入各自的桶中
- 使用分割函数对桶内的后缀进行排序
- 基于逐渐增长的前缀长度来细化排序
demo 字符串
old = "banana"
长度 oldsize = 6,再加一个哨兵 \0,总共参与排序的有 7 个后缀(包括空串):
| 索引 | 后缀 |
|---|---|
| 0 | banana |
| 1 | anana |
| 2 | nana |
| 3 | ana |
| 4 | na |
| 5 | a |
| 6 | ”“(空串) |
步骤1: 桶统计并排序(基于首字符)
我们统计每个字节的频次(ASCII):
'a'→ 3次'b'→ 1次'n'→ 2次
构造桶位置(以 ASCII 排序):
buckets['\0'] = 0
buckets['a'] = 1
buckets['b'] = 2
buckets['n'] = 3
步骤2:初始桶排序后缀位置
将后缀下标按其首字符放入 I 中:
| 字符 | 后缀起始位置 | 排序后 I 位置 |
|---|---|---|
| a | 1, 3, 5 | I[1], I[2], I[3] |
| b | 0 | I[4] |
| n | 2, 4 | I[5], I[6] |
再加上空串:
I[0] = 6 (空后缀的起始位置)
所以:
I = [6, 1, 3, 5, 0, 2, 4]
步骤3:初始化 V 数组(当前排序排名)
V[i] = 在 I 数组中 i 出现的位置
I = [6, 1, 3, 5, 0, 2, 4]
所以:
V[0] = 4 // "banana"
V[1] = 1 // "anana"
V[2] = 5 // "nana"
V[3] = 2 // "ana"
V[4] = 6 // "na"
V[5] = 3 // "a"
V[6] = 0 // ""(空串)
步骤4:进入迭代排序 refine(以 h=1,2,4…)
每一轮排序按 (rank[i], rank[i+h]) 的元组排序。
比如:
- 对于
h=1,我们比较每个后缀的前两个字符; split()函数就是在同一“段”内按这个二元组继续排序。
最终输出(后缀数组)
当排序稳定后,V[i] 就是后缀 i 的排名,而 I[rank] = 后缀位置。
即:
后缀: 排名 => I[rank] = 后缀起始位置
"" 0 => I[0] = 6
a 1 => I[1] = 5
ana 2 => I[2] = 3
anana 3 => I[3] = 1
banana 4 => I[4] = 0
na 5 => I[5] = 4
nana 6 => I[6] = 2
所以最终输出的 suffix array:
I = [6, 5, 3, 1, 0, 4, 2]
非常好的问题!你已经掌握了后缀数组 I 的生成过程,现在我们来回答核心问题:
字符串搜索与匹配
为什么 Suffix Array 能加速字符串匹配?
因为它将所有后缀按字典序排序了,我们就可以像查词典一样 用二分查找来匹配子串,从而大大减少搜索复杂度。
对于字符串 S = "banana",其后缀数组为:
I = [6, 5, 3, 1, 0, 4, 2]
表示的后缀排序为:
idx 后缀
---------------
6 ""
5 "a"
3 "ana"
1 "anana"
0 "banana"
4 "na"
2 "nana"
目标:快速判断子串是否在 S 中(如查找 "ana")
方法1(暴力):
- 枚举
S的每个后缀(共 n 个),对每个后缀做子串比较(长度为 m); - 时间复杂度 O(n × m)
方法2(用后缀数组):
- 所有后缀已经 排好序;
- 我们可以用 二分查找 找
"ana"; - 比较时只需最多 log(n) 次 + 最多 m 个字符比较;
这样匹配复杂度就变成 O(m × log n),比 O(nm) 快太多!
二分查找示例
我们要查找 pattern = "ana",在下列后缀中二分查找:
5 "a"
3 "ana"
1 "anana"
0 "banana"
4 "na"
2 "nana"
- 中间是 0 →
"banana",”ana” < “banana”,往左; - 然后查
3 → "ana",完全匹配,找到!
本质理解:后缀排序 = 有序前缀空间
Suffix Array 把所有可能的子串查找问题,降维为 一个有序集合中的子串前缀匹配问题。
再扩展一步:找所有匹配位置?
如果我们不是只要知道有没有 "ana",而是要知道它出现的位置呢?
你可以在后缀数组中找出所有以 "ana" 开头的后缀:
3 "ana" ← ✅
1 "anana" ← ✅
然后提取后缀起始下标 [3, 1] 就是所有匹配位置!
search 函数
主算法中
search 函数被用来为新文件中从 scan 位置开始的子串在旧文件中找到最佳匹配位置,返回匹配长度并通过 pos 参数返回匹配位置。
search函数内部:
采用二分搜索算法在已排序的后缀数组中查找匹配:
搜索逻辑分析
-
基础情况处理:当搜索范围缩小到2个元素以内时,直接比较两个候选位置的匹配长度,返回较长的匹配 bsdiff.c:149-160
-
二分搜索:选择中间位置进行字符串比较,根据比较结果决定搜索左半部分还是右半部分 bsdiff.c:162-167
-
匹配长度计算:使用 matchlen 函数计算实际的匹配长度 bsdiff.c:134-142
Diff 计算
bsdiff_internal 函数构建整个diff过程
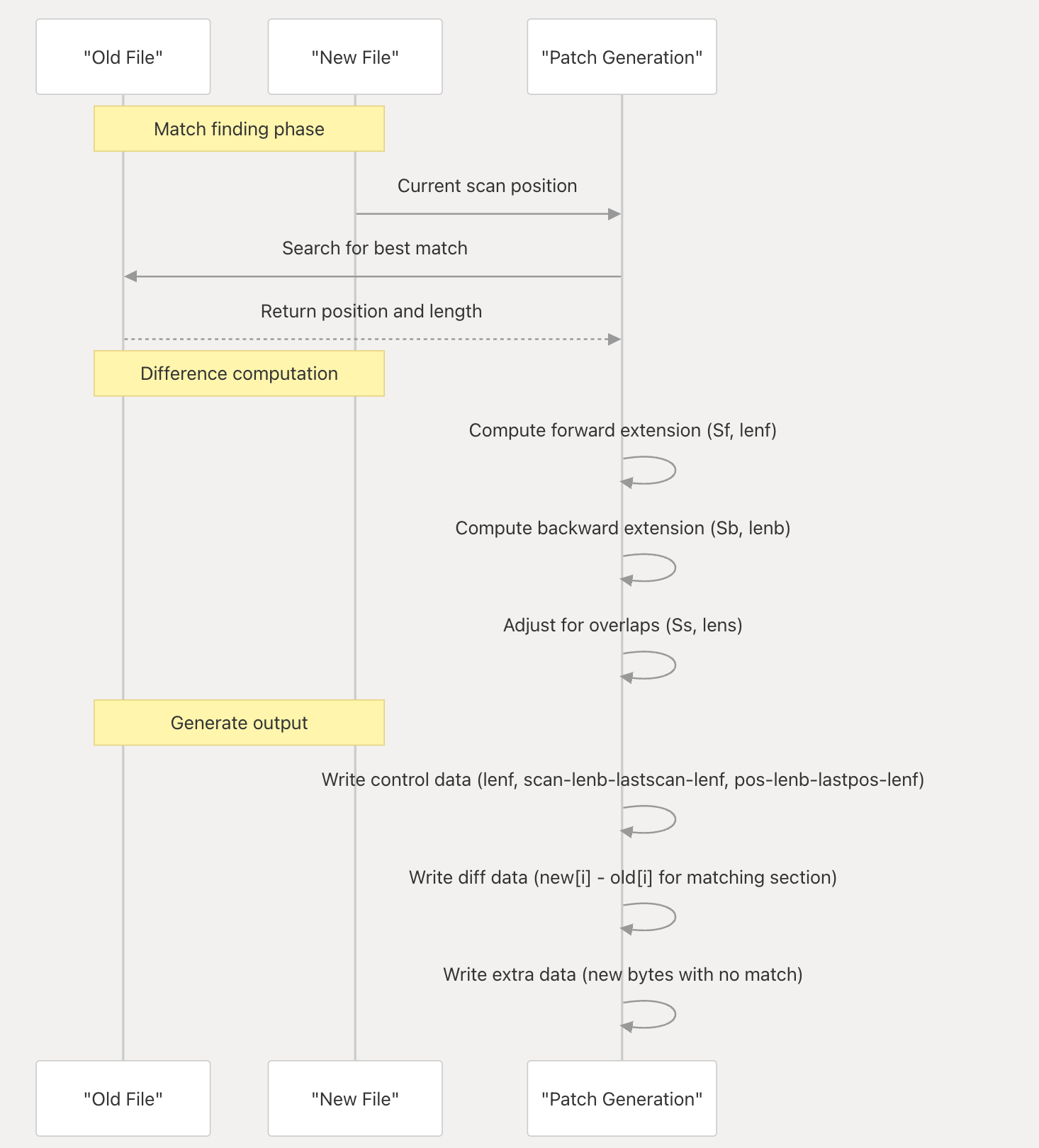
1. 前向扫描 (Sf, lenf)
前向扫描从上次处理的位置向前扩展匹配,寻找最佳扩展: bsdiff.c:264-269
这个循环比较 req.old[lastpos+i] 和 req.new[lastscan+i] 之间的字节,每次匹配时递增分数 s。算法使用公式 s2-i>Sf2-lenf 来找到最优扩展长度 lenf,该长度能最大化匹配与长度的比率。
2. 后向扫描 (Sb, lenb)
后向扫描从当前位置向后扩展匹配: bsdiff.c:272-278
这从当前的 scan 位置和找到的 pos 向后扫描,比较 req.old[pos-i] 与 req.new[scan-i]。它使用相同的优化公式 s2-i>Sb2-lenb 来找到最佳的后向扩展长度 lenb。
3. 重叠调整 (Ss, lens)
当前向和后向扩展重叠时,算法会解决这个问题以最小化补丁大小: bsdiff.c:280-293
重叠调整过程:
- 计算重叠区域:overlap=(lastscan+lenf)-(scan-lenb)
- 通过比较两个潜在匹配来评估重叠中的每个位置
- 找到最大化净收益的最优分割点 lens
- 调整边界:lenf+=lens-overlap 和 lenb-=lens
patch 补丁的生成
这些优化的边界随后用于生成三种类型的补丁数据:
控制数据:使用计算出的长度 bsdiff.c:295-301 差异数据:覆盖前向匹配的 lenf 字节 bsdiff.c:304-307 额外数据:处理前向和后向区域之间的间隙
note:
优化使用评分公式中的 2:1 比率(s*2-i)来平衡匹配质量和长度,即使匹配率稍低也偏好更长的匹配。这个启发式算法由 Colin Percival 在 commit bd08be73 中设计,有助于产生更紧凑的补丁
时间复杂度
- Suffix array construction 后缀数组构建: O(n log n), n是old file的大小
- 匹配和diff计算: O(m log n),m是new file 的大小
- 总复杂度: O((n+m) log n)
空间复杂度
- Suffix array: O(n)
- Additional buffers: O(n+m)
- Overall space usage: O(n+m)
空间复杂度
二进制打patch算法
在diff之后算出来,patch,再用patch打回去
old_file + patch -> new_file
二进制patch文件结构
- File Header: 文件头,包含 magic string “ENDSLEY/BSDIFF43” (16 bytes) 和 新文件的大小 (8 bytes)
- Control Data: 控制数据,每个控制快ctrl包含3个64位整数
- ctrl[0] - diff 数据的长度
- ctrl[1] - extra 数据的长度
- ctrl[2] - 旧文件位置的偏移调整量
- Diff Data: 新旧diff数据
- Extra Data: 额外的数据
流式数据接口
通过,bspatch_stream 接口 用流式读取 patch data
struct bspatch_stream
{
void* opaque; //这是一个不透明指针,用于存储客户端自定义的上下文数据。该字段在 bspatch 函数内部不会被读取或修改,完全由调用者控制,可以用来保存文件句柄、压缩状态或其他自定义数据。
int (*read)(const struct bspatch_stream* stream, void* buffer, int length); //该函数被 bspatch 调用来从流中读取二进制数据块。成功时返回 0,失败时返回非零值。
};
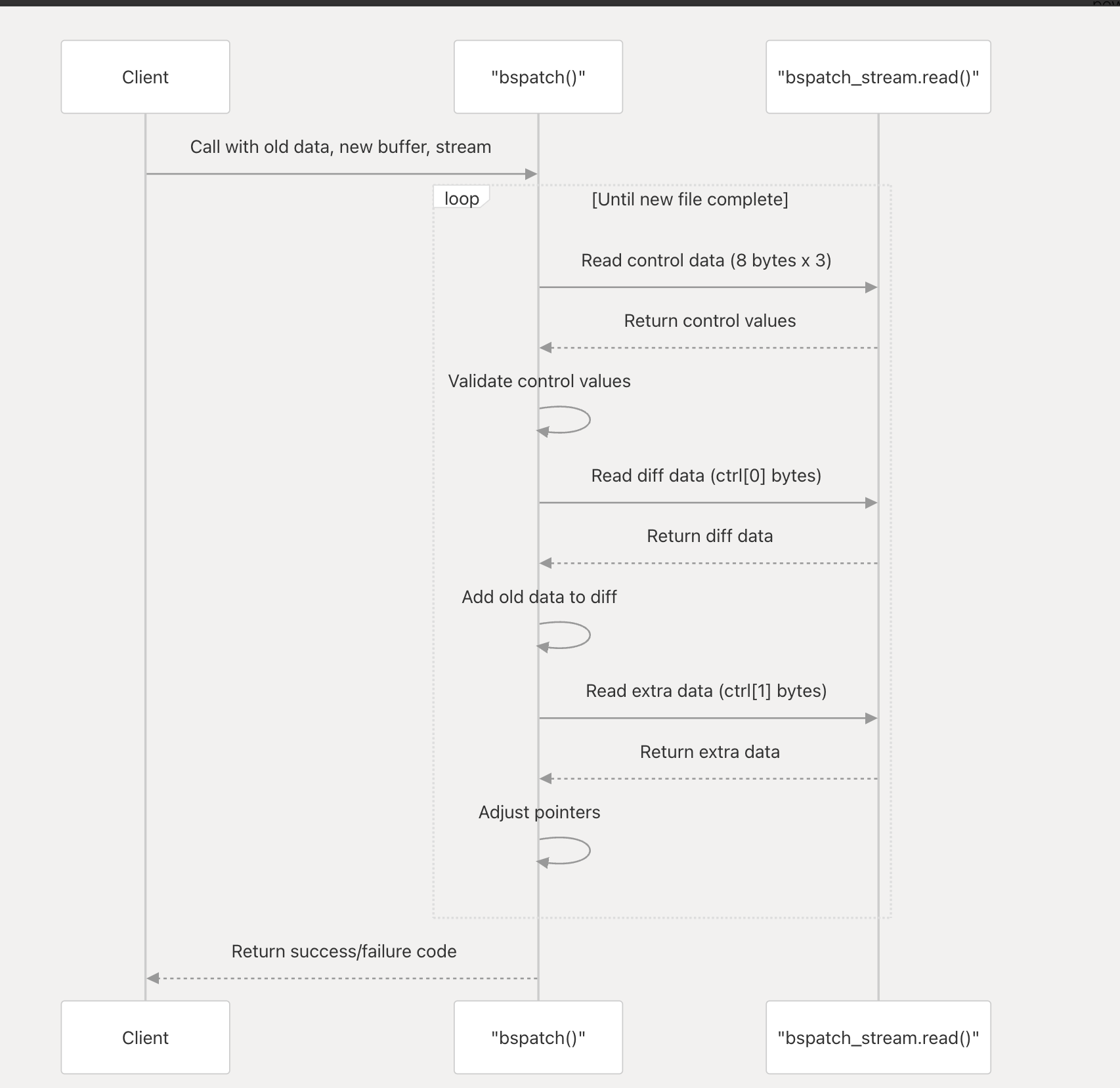
二进制patch算法
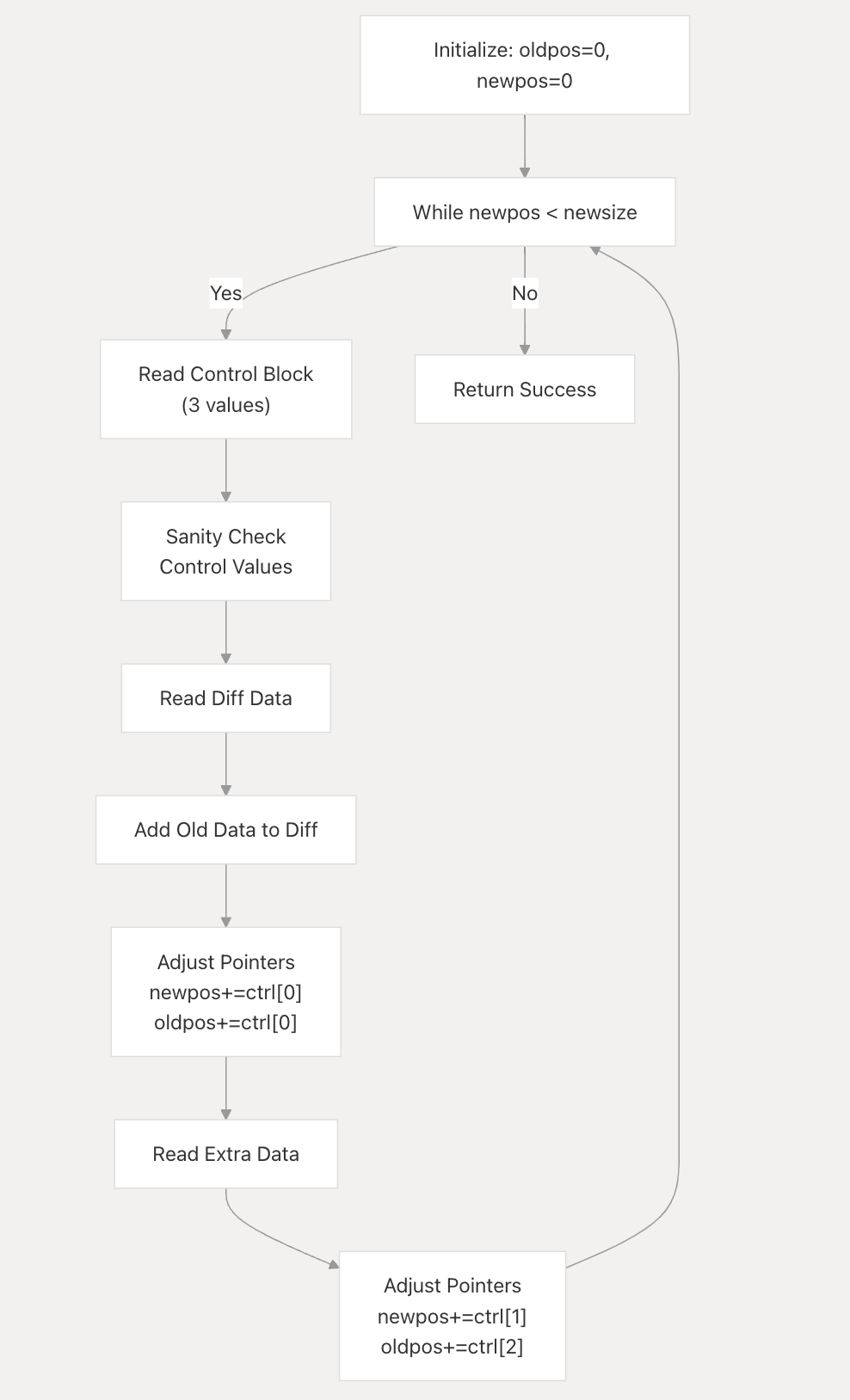
-
初始化指针:函数开始时将 oldpos 和 newpos 都设置为 0,这两个指针分别跟踪在旧文件和新文件中的当前位置。
-
循环处理补丁块 主循环持续执行直到 newpos 达到 newsize(新文件的总大小)。
- 读取三个控制值,ctrl[0], ctrl[1], ctrl[2]
- 控制值完整性检查
- 读取diff 数据长度:ctrl[0], 将旧文件中对应位置的字节加到差异数据,调整两个文件的位置指针
- 读取 extra 数据长度:ctrl[1], 再次调整位置指针,其中 oldpos 按 ctrl[2] 调整
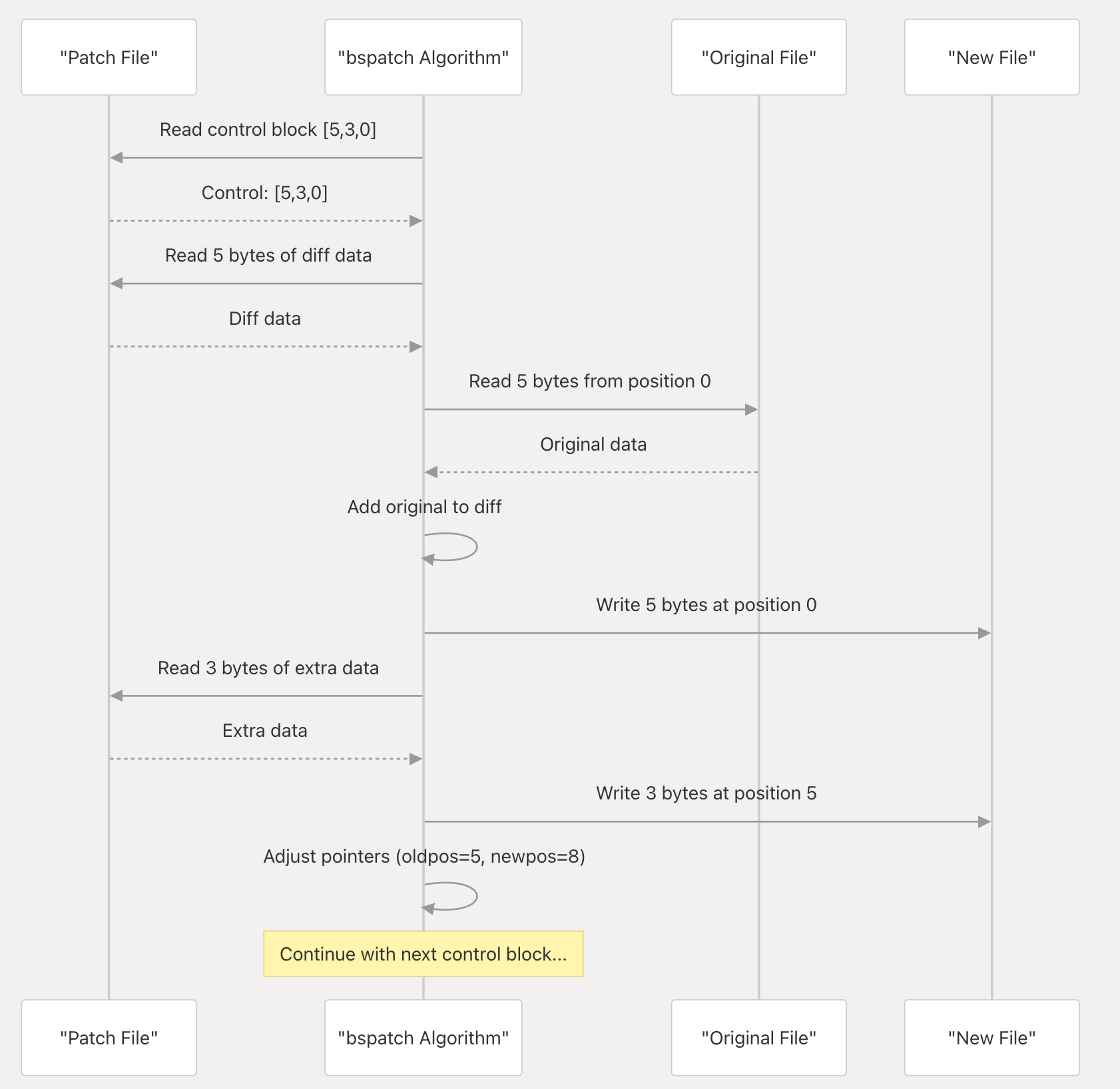
Integer 特殊处理:从字节序列到64位整数
为确保补丁文件中的控制数据在不同平台间能够正确解析,bsdiff/bspatch 采用固定的字节序格式来避免字节序差异问题。该机制包含两个核心函数:offtin(解码)和 offtout(编码)。
64位整数需要转换到 8个 uint8
offtin 函数:字节序列解码为64位整数
static int64_t offtin(uint8_t *buf)
{
int64_t y;
y=buf[7]&0x7F;
y=y*256;y+=buf[6];
y=y*256;y+=buf[5];
y=y*256;y+=buf[4];
y=y*256;y+=buf[3];
y=y*256;y+=buf[2];
y=y*256;y+=buf[1];
y=y*256;y+=buf[0];
if(buf[7]&0x80) y=-y;
return y;
}
核心机制:
- 字节序转换:按小端序(little-endian)格式将8字节缓冲区解码为64位整数
- 符号处理:使用最高位字节的符号位(buf[7] & 0x80)来确定正负性
- 解码顺序:从高位字节(buf[7])开始,逐步累积到低位字节(buf[0]) 在patch应用中的作用:
- offtin 用于读取补丁文件中的控制数据,每次迭代解析三个控制值来指导补丁应用过程。
offtout 函数 64位整数编码为字节序列
static void offtout(int64_t x,uint8_t *buf)
{
int64_t y;
if(x<0) y=-x; else y=x;
buf[0]=y%256;y-=buf[0];
y=y/256;buf[1]=y%256;y-=buf[1];
y=y/256;buf[2]=y%256;y-=buf[2];
y=y/256;buf[3]=y%256;y-=buf[3];
y=y/256;buf[4]=y%256;y-=buf[4];
y=y/256;buf[5]=y%256;y-=buf[5];
y=y/256;buf[6]=y%256;y-=buf[6];
y=y/256;buf[7]=y%256;
if(x<0) buf[7]|=0x80;
}
核心机制:
- 符号预处理:先取绝对值进行编码,负数标记延后处理
- 字节分解:通过取模和除法操作将64位整数分解为8个字节
-
符号标记:若原值为负数,则在最高位字节设置符号位(buf[7] = 0x80)