1. 序列解码(Sequence Decoding )概览
大语言模型在生成文本时,需要从词汇表中逐个选择 token 来组成完整的序列。 核心问题是:如何选择最优的 token 序列。
1.1 四种主要策略
1.1.1 朴素方案:穷举搜索(Exhaustive Search)
- 思路:尝试所有可能的 token 组合,找到概率最高的序列
-
复杂度: \(O(V^N)\) 其中
- $V$:词汇表大小(通常几万到十几万)
- $N$:序列长度
-
示例:词汇表 5 万,生成 10 个 token → (50000^{10}) 种可能
- 结论:完全不可行,计算成本天文数字。
1.1.2 贪心解码(Greedy Decoding)
- 思路:每一步都选择当前概率最高的 token
- 优点:速度快,复杂度 (O(N))
- 缺点:局部最优 ≠ 全局最优,容易错过更好的整体序列。
1.1.3 采样(Sampling)
- 思路:按概率分布随机采样 token,而非总选最高概率的。
- 特点:引入随机性,提升多样性与创造性。
-
常见变体:
- Top-k Sampling:只在前 k 个高概率 token 中采样
- Top-p Sampling(Nucleus Sampling):只在累计概率达到 p 的 token 集中采样。
1.1.4 束搜索(Beam Search)
- 思路:保留 k 个最有可能的候选序列,是贪心与穷举的折中。
- 特点:类似动态规划,在质量与效率间平衡。
- 参数:
beam_size控制保留的候选数量。
1.2 实际应用
| 任务类型 | 推荐策略 | 原因 |
|---|---|---|
| 事实性任务(翻译、摘要) | 贪心 / 束搜索 | 更稳定、确定性强 |
| 创造性任务(写作、对话) | 采样 | 提升生成多样性 |
2. Sampling(采样原理)
2.1 基本思想
不使用 \(\arg\max_y P(y|x)=f_\theta(x,y)\) 的方式,而是直接从分布 (P(Y|X)) 中随机采样出结果。
2.2 离散采样(Discrete Sampling)
设有 k 个类别,其概率为 (p_1, p_2, \dots, p_k)。从中采样 n 个值。
2.2.1 直接采样(Direct Sampling)
- 复杂度:O(nk)
- 方法:遍历所有 k 个类别,累加概率直到随机数落入对应区间。
- 缺点:每次采样都需遍历整个概率表。
2.2.2 二分查找采样(Binary Search Sampling)
- 复杂度:O(k + n log k)
-
方法:
- 构建累积概率分布(O(k))
- 使用二分查找定位随机数对应类别(O(log k))
- 优势:比直接采样更快。
2.2.3 别名采样(Alias Sampling)
- 复杂度:O(k log k + n)
-
方法:
- 构建别名表(Alias Table,O(k log k))
- 采样阶段每次 O(1) 时间完成。
- 优势:适合大量重复采样场景,是最快方案。
3. 束搜索算法(Beam Search Algorithm)
3.1 算法步骤
3.1.1 初始化
S = {} # 候选集初始化为空
3.1.2 保留 k 个最佳部分序列
- k = beam size(束宽)
- 只保留概率最高的 k 条路径,丢弃其他。
3.1.3 向前扩展
- 每条序列扩展出 V 个候选(V = 词汇表大小)
- 共生成 k×V 个新候选。
3.1.4 筛选与迭代
- 从 k×V 个候选中选出 top-k
- 作为下一轮候选集
- 重复至生成
<END>。
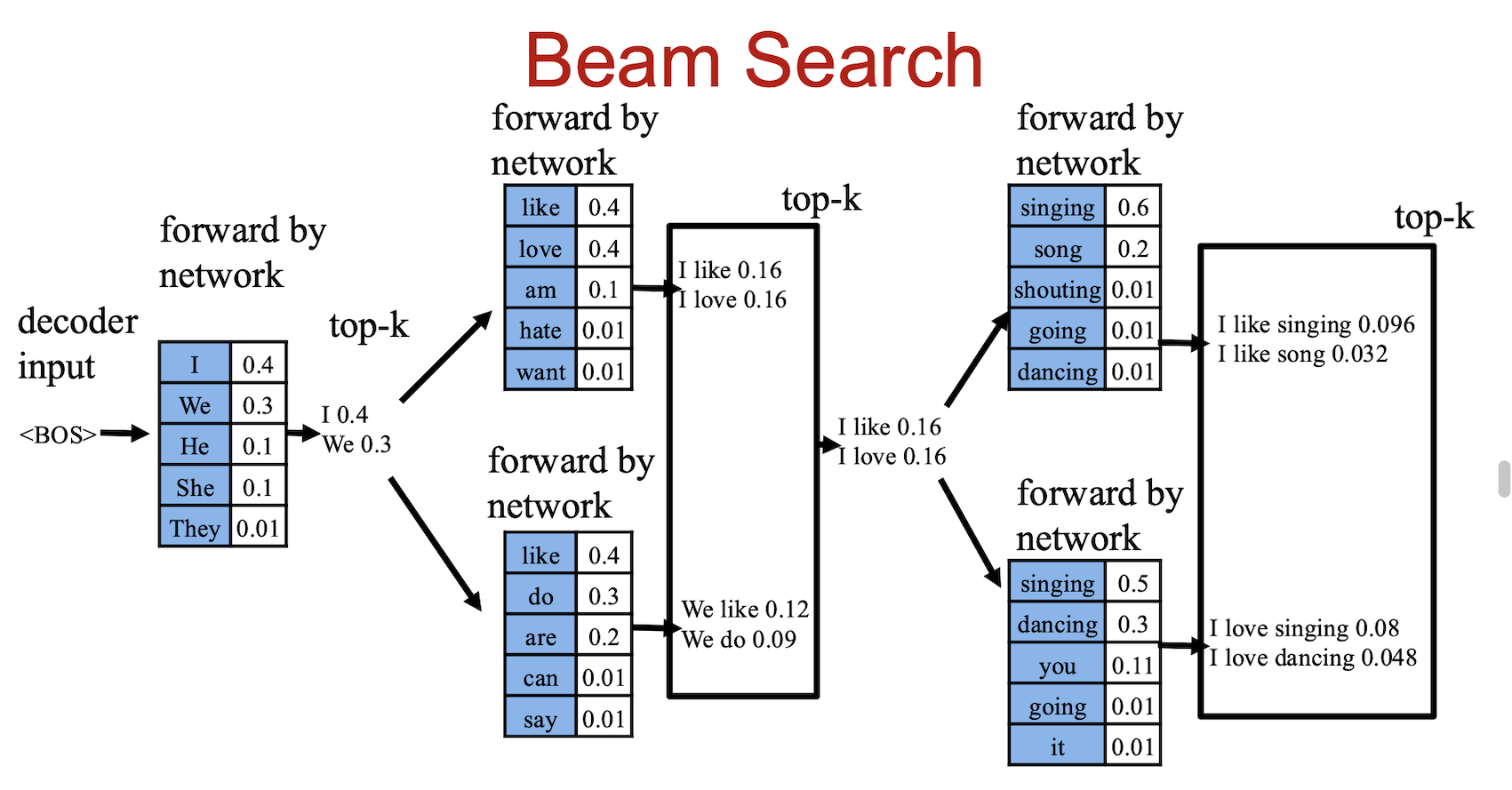
3.2 图解示例
假设 beam size = 2,词汇表包含 3 个词:
步骤1: S = {<START>}
步骤2: 扩展出3个候选
<START> → "我" (P=0.6)
<START> → "吾" (P=0.3)
<START> → "本" (P=0.1)
步骤3: 保留top-2
S = {"我", "吾"}
步骤4: 继续扩展
"我" → "我爱" (P=0.6×0.5=0.30)
"我" → "我很" (P=0.6×0.3=0.18)
"吾" → "吾爱" (P=0.3×0.9=0.27)
...
步骤5: 保留top-2
S = {"我爱", "吾爱"}
3.3 关键特性总结
| 项目 | 内容 |
|---|---|
| 优点 | 比贪心更接近全局最优,比穷举高效 |
| 复杂度 | 时间 O(N×k×V),空间 O(k) |
| 与贪心关系 | 贪心是 beam size=1 的特例 |
| 常用参数 | 翻译 k=5~10;摘要 k=3~5;对话多用采样 |
直观理解:k 越大 → 越接近全局最优,但计算代价也越高。
3.4 示例伪代码
best_scores = []
add {[0], 0.0} to best_scores # 0 表示起始token
for i in range(1, max_length):
new_seqs = PriorityQueue()
for (candidate, s) in best_scores:
if candidate[-1] is EOS:
prob = all -inf
prob[EOS] = 0
else:
prob = model.predict(candidate)
# 取 top-k
for score, idx in top_k(prob):
new_seq = candidate + [idx]
new_score = s + score
new_seqs.put((new_seq, new_score))
best_scores = top_k(new_seqs, k)
4. Beam Search 的剪枝(Pruning)
为减少无效计算,可对低分候选进行剪枝。
4.1 相对阈值剪枝(Relative Threshold Pruning)
4.1 相对阈值剪枝(Relative Threshold Pruning)
- 规则: [ score(cand) ≤ rp × \max{score(c)} ]
-
参数:
- rp ∈ (0, 1),相对阈值
- 示例:
| 候选 | 分数 | 保留 |
|---|---|---|
| A | 0.8 | ✅ |
| B | 0.5 | ✅ |
| C | 0.09 | ✅ |
| D | 0.07 | ❌ |
(rp=0.1,阈值=0.08)
4.2 绝对阈值剪枝(Absolute Threshold Pruning)
- 规则: [ score(cand) ≤ \max{score(c)} - ap ]
- 示例(ap=0.3):
| 候选 | 分数 | 保留 |
|---|---|---|
| A | 0.8 | ✅ |
| B | 0.6 | ✅ |
| C | 0.4 | ❌ |
| D | 0.3 | ❌ |
特点:固定差值,更直观但可能不适合 log 概率。
4.3 相对局部阈值剪枝(Relative Local Threshold Pruning)
参考论文: Freitag & Al-Onaizan, 2017 — “Beam Search Strategies for Neural Machine Translation”
5. 采样与 Beam Search 的结合
-
策略:
- 先使用 采样 (Sampling) 生成若干起始 token
- 然后对每个样本继续执行 Beam Search
-
目的:
- 提升序列多样性
- 减少完全确定性带来的重复性