GPU加速策略

1 GPU 加速技术概览（GPU Acceleration Tech）

1.1 主要方向

Tiling（分块）
Memory Parallelism（内存并行）
GPU 上的矩阵乘法加速
稀疏矩阵乘法（Sparse MatMul）
cuBLAS 库使用

2 GPU 上的矩阵乘法基础示例

__global__ void MatMulKernel(float *a, float *b, float *c, int N) {
    // Compute each thread's global row and col index -> output: (i, j)
    int row = blockIdx.y * blockDim.y + threadIdx.y;
    int col = blockIdx.x * blockDim.x + threadIdx.x;
    if (row >= N || col >= N) return;
    float Pvalue = 0.0;
    for (int k = 0; k < N; k++) {
        Pvalue += a[row * N + k] * b[k * N + col];
    }
    c[row * N + col] = Pvalue;
}

2.1 每次迭代的操作

1次 FP32 乘法: a[...] * b[...]
1次 FP32 加法: Pvalue +=
2次全局内存访问: 分别读取 a 和 b（每次 4 字节）

2.2 计算强度（Compute-to-Global-Memory-Access Ratio）

\[\text{计算强度} = \frac{2\ \text{FLOP}}{2 \times 4\ \text{Bytes}} = 0.25\ \text{FLOP/Byte}\]

这表示：

每从内存读取 1字节数据，只执行 0.25次浮点运算
或者说：每执行 1次运算，需要传输 4字节数据

结论：

算法为内存密集型
GPU 计算单元大部分时间在等待数据
优化方向：使用共享内存、分块（Tiling）等技术提升计算强度

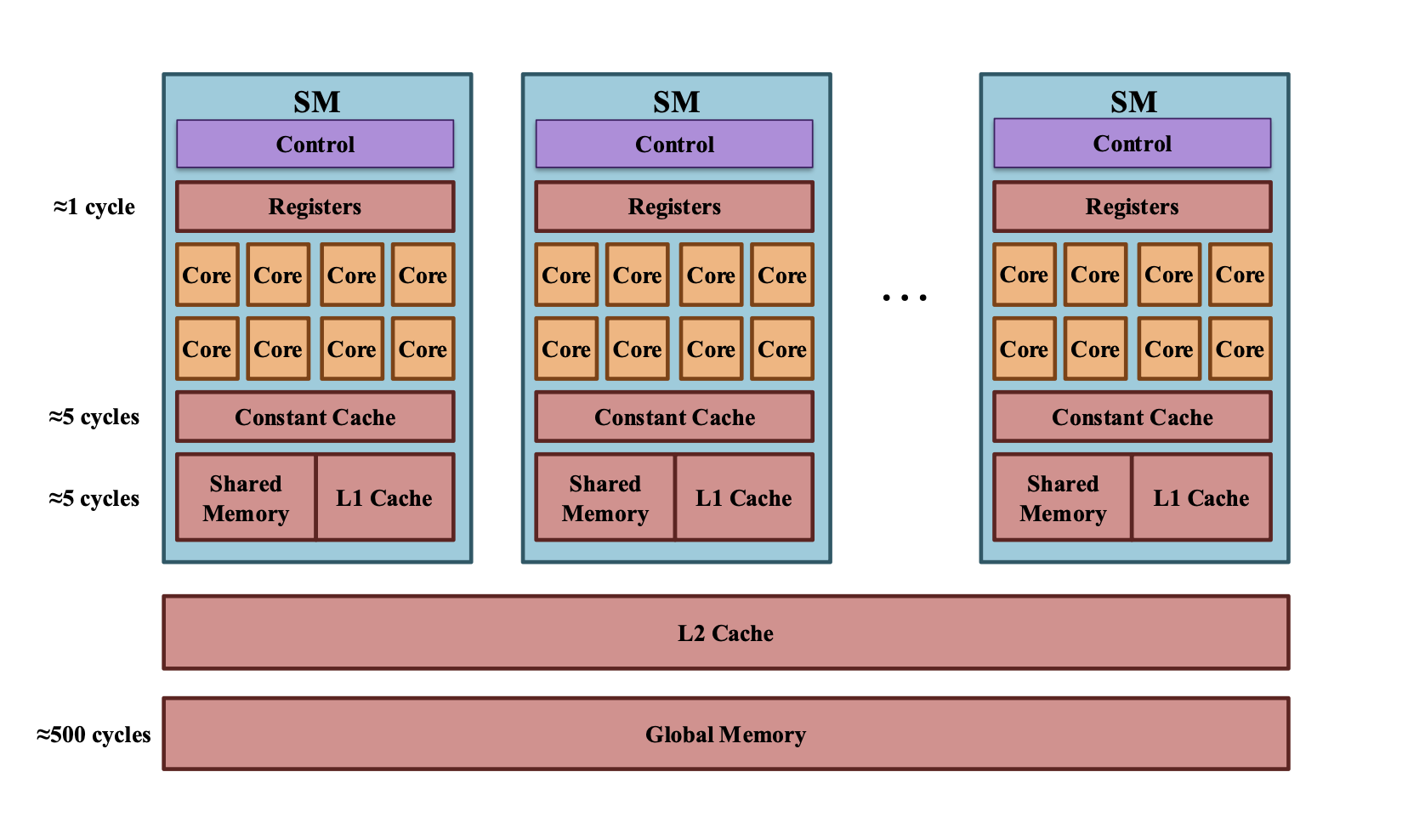
alt text

其中cycle 是时钟周期

3 加载 vs 计算的性能对比

3.1 示例代码

C[i] = A[i] + B[i];

简单的向量加法操作

3.2 GPU 指令时间开销

(1) 内存加载指令 — 极慢

ld.global.f32 %f1, [%rd1];  // 加载 A[i] → 500 cycles
ld.global.f32 %f2, [%rd2];  // 加载 B[i] → 500 cycles

从全局内存读取数据
每次加载耗时约 500个时钟周期
总加载时间：1000 cycles

(2) 计算指令 — 极快

add.f32 %f3, %f1, %f2;      // 执行加法    → 1 cycle

浮点加法运算
仅需 1个时钟周期

(3) 存储指令

st.global.f32 [%rd3], %f3;

3.3 时间对比

时间对比

| 操作类型 | 耗时 (cycles) | | —- | ———– | | 数据加载 | 1000 (500 + 500) | | 实际计算 | 1 |

比值：1000 : 1

3.4 关键洞察

“Loading data takes more time than actual computation!” 加载数据的时间远超实际计算时间！

3.5 实际意义

这个例子清晰展示了：

内存墙问题：GPU 性能瓶颈在于数据传输
计算单元浪费：多数时间 GPU 在等待数据
优化方向：
- 减少全局内存访问次数
- 使用共享内存/寄存器缓存数据
- 提高数据重用率
- 增加计算强度

这就是为什么优化GPU程序的核心是优化内存访问模式，而不仅仅是优化算法本身

4 CUDA 设备内存模型

4.1 内存层次结构（从快到慢）

4.1.1 寄存器（Registers）- 最快

作用域: 每个线程私有
访问权限: 读/写（R/W per-thread）
特点:
- 速度最快（1 cycle）
- 数量有限
- 自动分配给线程的局部变量

4.1.2 局部内存（Local Memory）

作用域: 每个线程私有
访问权限: 读/写（R/W per-thread）
特点:
- 实际存储在全局内存中
- 用于寄存器溢出的数据
- 速度较慢

4.1.3 共享内存（Shared Memory）- 重要优化工具

作用域: 每个线程块内共享
访问权限: 读/写（R/W per-block）
特点:
- 速度快（比全局内存快约100倍）
- 同一块内的所有线程可访问
- 用于线程间数据共享和缓存
- 橙色区域显示在图中

4.1.4 全局内存（Global Memory）- 最慢但最大

作用域: 整个Grid可访问
访问权限: 读/写（R/W per-grid）
特点:
- 容量大（GB级）
- 速度慢（~500 cycles）
- 所有线程都可访问
- Host可以传输数据到此

4.1.5 常量内存（Constant Memory）

作用域: 整个Grid可访问
访问权限: 只读（Read only per-grid）
特点:
- 有缓存机制
- 适合广播相同数据给所有线程
- Host负责写入

类型	作用域	访问权限	特点
寄存器（Registers）	每线程	R/W	最快（1 cycle），数量有限
局部内存（Local Memory）	每线程	R/W	存储寄存器溢出数据，速度慢
共享内存（Shared Memory）	每块	R/W	比全局内存快约100倍，块内共享
全局内存（Global Memory）	全Grid	R/W	容量大（GB级），速度慢（~500 cycles）
常量内存（Constant Memory）	全Grid	只读	适合广播数据，有缓存

4.2 数据流向

Host ←→ Global Memory / Constant Memory
         ↕
    Thread Registers
         ↕
    Shared Memory (块内共享)

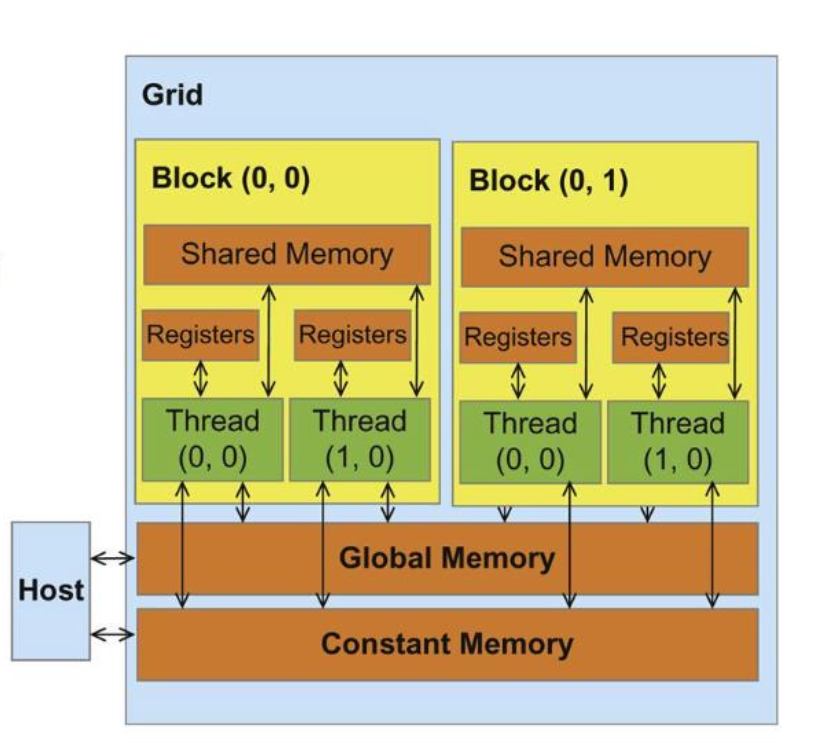
alt text

速度排序： \(Registers > Shared\ Memory >> Global\ Memory\)

4.3 CUDA设备内存访问

Variable declaration	Memory	Scope	Lifetime
`int var;`	Register	Thread	Grid
`int varArr[N];`	Local	Thread	Grid
`__device__ __shared__ int SharedVar;`	Shared	Block	Grid
`__device__ int GlobalVar;`	Global	Grid	Application
`__device__ __constant__ int constVar;`	Constant	Grid	Application

Register: 普通局部变量，自动分配到寄存器
Local: 数组或寄存器溢出的变量，存储在局部内存
Shared: 使用 __shared__ 修饰符，块内线程共享
Global: 使用 __device__ 修饰符，全局可访问
Constant: 使用 __device__ __constant__ 修饰符，只读全局内存

5 Tiled矩阵乘法优化详解

代码：https://github.com/llmsystem/llmsys_code_examples/blob/main/cuda_acceleration_demo/matmul_tile_full.cu

5.1 优化思想

使用 分块 (Tiling) 与 共享内存 (Shared Memory) 减少全局内存访问次数。

5.2 优化对比

5.2.1 原始版本的问题

for (int k = 0; k < N; k++) {
    Pvalue += d_A[row * N + k] * d_B[k * N + col];  
    // 每次迭代访问2次全局内存（慢500 cycles）
}

计算一个元素需要访问全局内存 2N次
总访问次数：N² × 2N = 2N³

5.2.2 Tiled版本的优化

// 1. 将数据加载到共享内存（快速缓存）
As[threadIdx.y][threadIdx.x] = d_A[...];  // 只加载1次
Bs[threadIdx.y][threadIdx.x] = d_B[...];  // 只加载1次

// 2. 从共享内存读取（快100倍）
for(int k = 0; k < TILE_WIDTH; ++k) {
    Cvalue += As[threadIdx.y][k] * Bs[k][threadIdx.x];
}

5.3 详细工作流程

5.3.1 数据分块加载

for(int ph = 0; ph < N/TILE_WIDTH; ++ph) {  // 分成 N/TILE_WIDTH 个phase

将N×N矩阵分成多个 TILE_WIDTH × TILE_WIDTH 的小块
每个phase处理一对对应的tile

5.3.2 协作加载到共享内存

As[threadIdx.y][threadIdx.x] = d_A[row * N + ph * TILE_WIDTH + threadIdx.x];
Bs[threadIdx.y][threadIdx.x] = d_B[(ph * TILE_WIDTH + threadIdx.y) * N + col];
__syncthreads();  // 确保所有线程都加载完成

每个线程负责加载1个元素到共享内存
整个block协作加载 TILE_WIDTH² 个元素
__syncthreads() 确保数据就绪后再计算

5.3.3 使用共享内存计算

for(int k = 0; k < TILE_WIDTH; ++k) {
    Cvalue += As[threadIdx.y][k] * Bs[k][threadIdx.x];
}
__syncthreads();  // 确保计算完成再加载下一块

从共享内存读取（快）
重复使用已加载的数据

5.4 性能提升分析

5.4.1 内存访问次数对比

版本	全局内存访问	共享内存访问
简单版本	2N次/元素	0
Tiled版本	2N/TILE_WIDTH次/元素	2N次/元素

5.4.2 具体示例（N=1024, TILE_WIDTH=16）

简单版本：

每个元素访问全局内存：2 × 1024 = 2048次

Tiled版本：

全局内存访问：2 × 1024/16 = 128次
共享内存访问：2 × 1024 = 2048次（但快100倍）

加速比：2048/128 = 16倍 全局内存访问减少

5.4.3 计算强度提升

简单版本：

0.25 FLOP/Byte (每8字节做2次运算)

Tiled版本：

假设TILE_WIDTH=16:
- 每次加载 16×16×2 = 512个float = 2048 Bytes
- 执行 16×16×16×2 = 8192 次运算
- 计算强度 = 8192/2048 = 4 FLOP/Byte

提升了16倍

5.5 关键技术点

1. `shared` 共享内存

__shared__ float As[TILE_WIDTH][TILE_WIDTH];
__shared__ float Bs[TILE_WIDTH][TILE_WIDTH];

片上内存，访问延迟低（~1-5 cycles vs 500 cycles）
Block内所有线程共享

2. `__syncthreads()` 同步

__syncthreads();  // 屏障同步

确保block内所有线程执行到此处
第一次：确保数据加载完成
第二次：确保计算完成，避免数据竞争

3. 数据重用

每个tile的数据被TILE_WIDTH个线程重复使用
As的每一行被使用TILE_WIDTH次
Bs的每一列被使用TILE_WIDTH次

6 内存限制 (Memory Restriction)

6.1 寄存器限制

寄存器限制

假设GPU有：

总寄存器数: 16384个
线程数: 1024个

每个线程可用寄存器： \(\text{每线程可用寄存器数} = \frac{16384}{1024} = 16\)

影响: 如果kernel使用超过16个寄存器，实际能并发运行的线程数会减少，降低occupancy（占用率）

6.2 共享内存限制

每个 Block 最多 192KB 共享内存

这是硬件限制，无法超越

例如 TILE_WIDTH=32： \(2 \times 32 \times 32 \times 4 = 8\text{KB} < 192\text{KB} \ \text{(可行)}\)

6.3关键启示

6.3.1 为什么要关心这些限制

Tile size不能无限大
如果 As + Bs 超过192 KB，kernel无法运行
需要在tile size和occupancy之间权衡

6.3.2 实际影响

假设想用 TILE_WIDTH = 64：

As: 64 × 64 × 4 = 16 KB
Bs: 64 × 64 × 4 = 16 KB
总计: 32 KB  ✅ 仍然OK

假设想用 TILE_WIDTH = 256：

As: 256 × 256 × 4 = 256 KB  ❌ 超过192 KB限制！

常用TILE_WIDTH: 16, 32, 64
32是一个常见的平衡选择
太小：性能提升有限
太大：可能超出共享内存限制或降低occupancy

7 内存并行与访问局部性

Locality / Bursts Organization 局部排布/交错排除 • Consecutive memory 顺序读取 accesses in a warp are coalesced together. • Row-major format to store multidimensional array in C and CUDA • allows DRAM burst, faster than individual acces

7.1 合并访问 (Coalesced Access)

定义: Warp内连续的内存访问会被合并成单次事务

7.1.1 什么是Warp

32个线程为一组，同时执行相同指令
GPU调度的基本单位

7.1.2 合并访问示例

// 好模式  - Coalesced
int idx = threadIdx.x;
float val = data[idx];  // Thread 0访问data[0], Thread 1访问data[1]...

结果：

32个线程访问连续的32个元素
GPU合并成1次内存事务（128字节）
高效！

// 坏模式  - Non-coalesced  
int idx = threadIdx.x * 32;
float val = data[idx];  // Thread 0访问data[0], Thread 1访问data[32]...

结果：

32个线程访问分散的位置
GPU需要32次独立内存事务
慢32倍！

7.2 行主序 (Row-Major Format)

7.2.1 C/CUDA的多维数组存储方式

float A[4][3];  // 4行3列

内存布局（行主序）：

[A00 A01 A02 | A10 A11 A12 | A20 A21 A22 | A30 A31 A32]
 ←-- Row 0 --→  ←-- Row 1 --→  ←-- Row 2 --→  ←-- Row 3 --→

关键: 同一行的元素在内存中连续存储

7.2.2 访问模式的影响

高效访问（按行）

int row = blockIdx.y * blockDim.y + threadIdx.y;
int col = blockIdx.x * blockDim.x + threadIdx.x;

// Warp内线程访问同一行的连续元素
float val = A[row * N + col];  
// Thread 0: A[row][0]
// Thread 1: A[row][1]
// Thread 2: A[row][2]  连续！

低效访问（按列）

// Warp内线程访问同一列的元素
float val = A[col * N + row];
// Thread 0: A[0][col]
// Thread 1: A[1][col]  
// Thread 2: A[2][col]  跨行访问，不连续！

7.3 DRAM 突发模式 (Burst Access)

7.3.1 什么是DRAM Burst？**

现代DRAM设计为批量传输数据更高效：

单次访问：

请求1个字节 → 传输1个字节
延迟高 (~500 cycles)

突发访问：

请求连续128字节 → 一次性传输128字节
延迟仍是 ~500 cycles
但吞吐量提升128倍！

7.3.2 为什么突发访问快？

┌─────────────────────────────────────┐
│  DRAM Bank                          │
│  [连续数据块: 128 bytes]            │
│  一次激活传输整块                    │
└─────────────────────────────────────┘

vs.

┌─────────────────────────────────────┐
│  DRAM Bank                          │
│  [分散访问需要多次激活]             │
│  每次激活开销相同                    │
└─────────────────────────────────────┘

7.4 实际应用示例

Tiled矩阵乘法中的合并访问

// 加载A到共享内存（行主序访问）
As[threadIdx.y][threadIdx.x] = 
    d_A[row * N + ph * TILE_WIDTH + threadIdx.x];
    //   ↑ row固定         ↑ threadIdx.x连续变化
    // Warp内线程访问连续地址！

// 加载B到共享内存
Bs[threadIdx.y][threadIdx.x] = 
    d_B[(ph * TILE_WIDTH + threadIdx.y) * N + col];
    //    ↑ threadIdx.y变化  ↑ col固定
    // 跨步访问 - 但只加载一次！

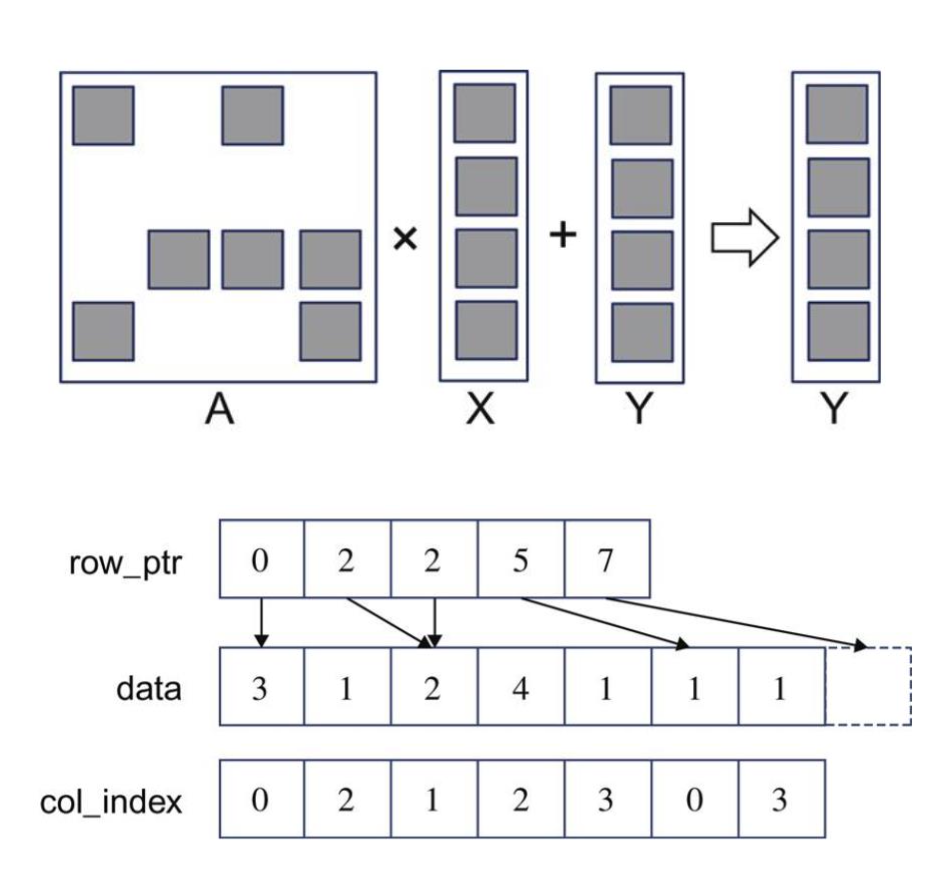
8 稀疏矩阵乘法 (Sparse Matrix Multiplication)

8.1 CSR 格式

Compressed Sparse Row (CSR)：仅存储非零元素
三个数组：
- data[]：非零元素
- col_index[]：列索引
- row_ptr[]：行边界

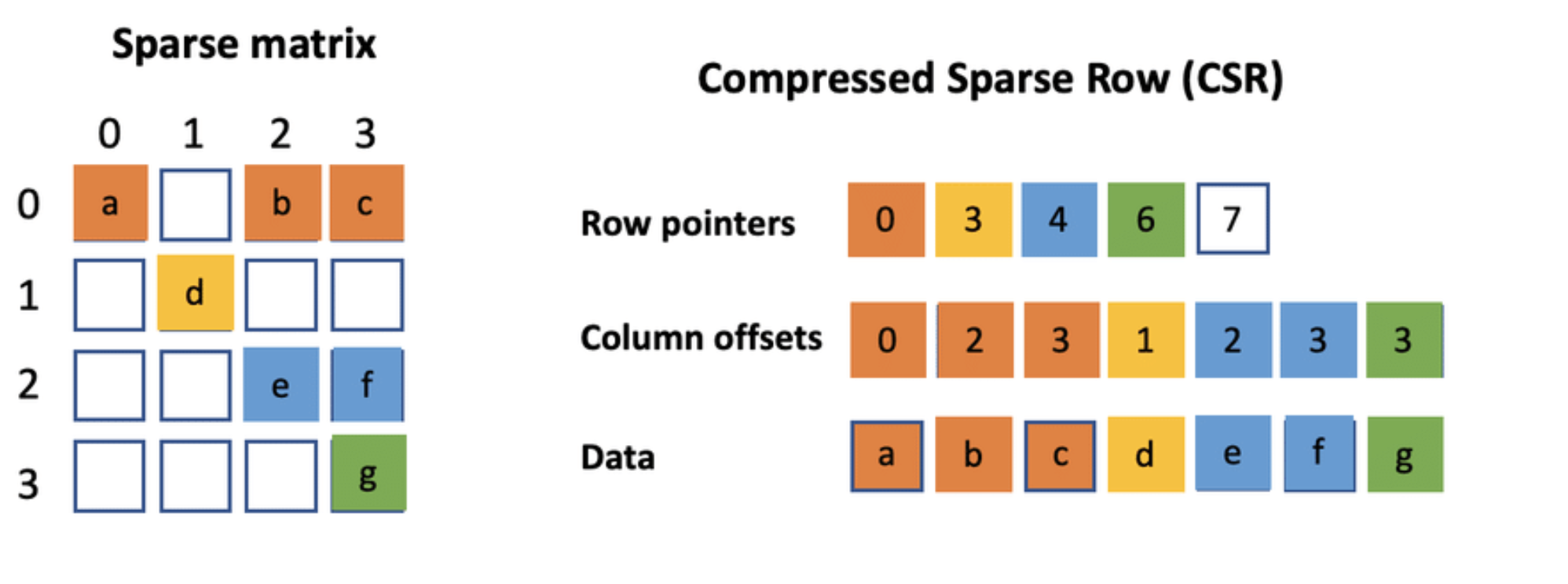
alt text

8.2 代码实现

稀松 Sparse Matrix-Vector Multiplication

伪代码：

for(int row = 0; row < n; row++) {
  float dot = 0;
  int row_start = row_ptr[row];
  int row_end = row_ptr[row + 1];
  for(int el = row_start; el < row_end; el++)
  {
    dot += x[el] * data[col_index[el]];
  }
  y[row] += dot;
}

GPU 实现：

__global__ void SpMVCSRKernel(float *data, int *col_index, int *row_ptr, float *x, float *y, int
num_rows) {
  int row = blockIdx.x * blockDim.x + threadIdx.x;
  if(row < num_rows) {
  float dot = 0;
  int row_start = row_ptr[row];
  int row_end = row_ptr[row + 1];
  for(int elem = row_start; elem < row_end; elem++) {
    dot += x[row] * data[col_index[elem]];
  }
  y[row] += dot;
  }
}

alt text

9 cuBLAS 库使用简介

Subroutine）** 是用于 矩阵与向量运算 (GEMM) 的高性能库。

\[C = \alpha A \times B + \beta C\]

a lightweight library dedicated to GEneral Matrix-to-matrix Multiply (GEMM)

的核心用途是执行 GEMM 运算： GEMM = GEneral Matrix to Matrix Multiply，即通用矩阵乘法

9.2 常用 API

9.2.1 初始化与销毁

• must call before:

cublasStatus_t cublasCreate(cublasHandle_t *handle)

• must call after:

cublasStatus_t cublasDestroy(cublasHandle_t handle)

9.2.2 向量点积

• float vector dot product

cublasStatus_t cublasSdot (cublasHandle_t handle, int n,
        const float *x, int incx,
        const float *y, int incy,
        float *result)

9.2.3 矩阵向量乘法

\(y = \alpha A x + \beta y\)

cublasStatus_t cublasSgemv(cublasHandle_t handle,
                  cublasOperation_t trans,
                  int m, int n,
                  const float *alpha,
                  const float *A, int lda,
                  const float *x, int incx,
                  const float *beta,
                  float *y, int incy)

9.2.4 矩阵乘法

\[C = \alpha A B + \beta C\]

cublasStatus_t cublasSgemm(cublasHandle_t handle,
          cublasOperation_t transa,
          cublasOperation_t transb,
          int m, int n, int k, const float *alpha,
          const float *A, int lda,
          const float *B, int ldb,
          const float *beta,
          float *C, int ldc)

参考代码： llmsys_code_examples/cuda_acceleration_demo/matmul_tile_full.cu

上篇LLM的decoding

下篇transformer的加速策略

1 GPU 加速技术概览（GPU Acceleration Tech）

1.1 主要方向

2 GPU 上的矩阵乘法基础示例

2.1 每次迭代的操作

2.2 计算强度（Compute-to-Global-Memory-Access Ratio）

3 加载 vs 计算的性能对比

3.1 示例代码

3.2 GPU 指令时间开销

(1) 内存加载指令 — 极慢

(2) 计算指令 — 极快

(3) 存储指令

3.3 时间对比

时间对比

3.4 关键洞察

3.5 实际意义

4 CUDA 设备内存模型

4.1 内存层次结构（从快到慢）

4.1.1 寄存器（Registers）- 最快

4.1.2 局部内存（Local Memory）

4.1.3 共享内存（Shared Memory）- 重要优化工具

4.1.4 全局内存（Global Memory）- 最慢但最大

4.1.5 常量内存（Constant Memory）

4.2 数据流向

4.3 CUDA设备内存访问

5 Tiled矩阵乘法优化详解

5.1 优化思想

5.2 优化对比

5.2.1 原始版本的问题

5.2.2 Tiled版本的优化

5.3 详细工作流程

5.3.1 数据分块加载

5.3.2 协作加载到共享内存

5.3.3 使用共享内存计算

5.4 性能提升分析

5.4.1 内存访问次数对比

5.4.2 具体示例（N=1024, TILE_WIDTH=16）

5.4.3 计算强度提升

5.5 关键技术点

1. __shared__ 共享内存

2. __syncthreads() 同步

3. 数据重用

6 内存限制 (Memory Restriction)

6.1 寄存器限制

寄存器限制

6.2 共享内存限制

6.3关键启示

6.3.1 为什么要关心这些限制

6.3.2 实际影响

7 内存并行与访问局部性

7.1 合并访问 (Coalesced Access)

7.1.1 什么是Warp

7.1.2 合并访问示例

7.2 行主序 (Row-Major Format)

7.2.1 C/CUDA的多维数组存储方式

7.2.2 访问模式的影响

7.3 DRAM 突发模式 (Burst Access)

7.3.1 什么是DRAM Burst？**

7.3.2 为什么突发访问快？

7.4 实际应用示例

8 稀疏矩阵乘法 (Sparse Matrix Multiplication)

8.1 CSR 格式

8.2 代码实现

9 cuBLAS 库使用简介

9.2 常用 API

9.2.1 初始化与销毁

9.2.2 向量点积

9.2.3 矩阵向量乘法

9.2.4 矩阵乘法

1. `shared` 共享内存

2. `__syncthreads()` 同步