FP8 精度
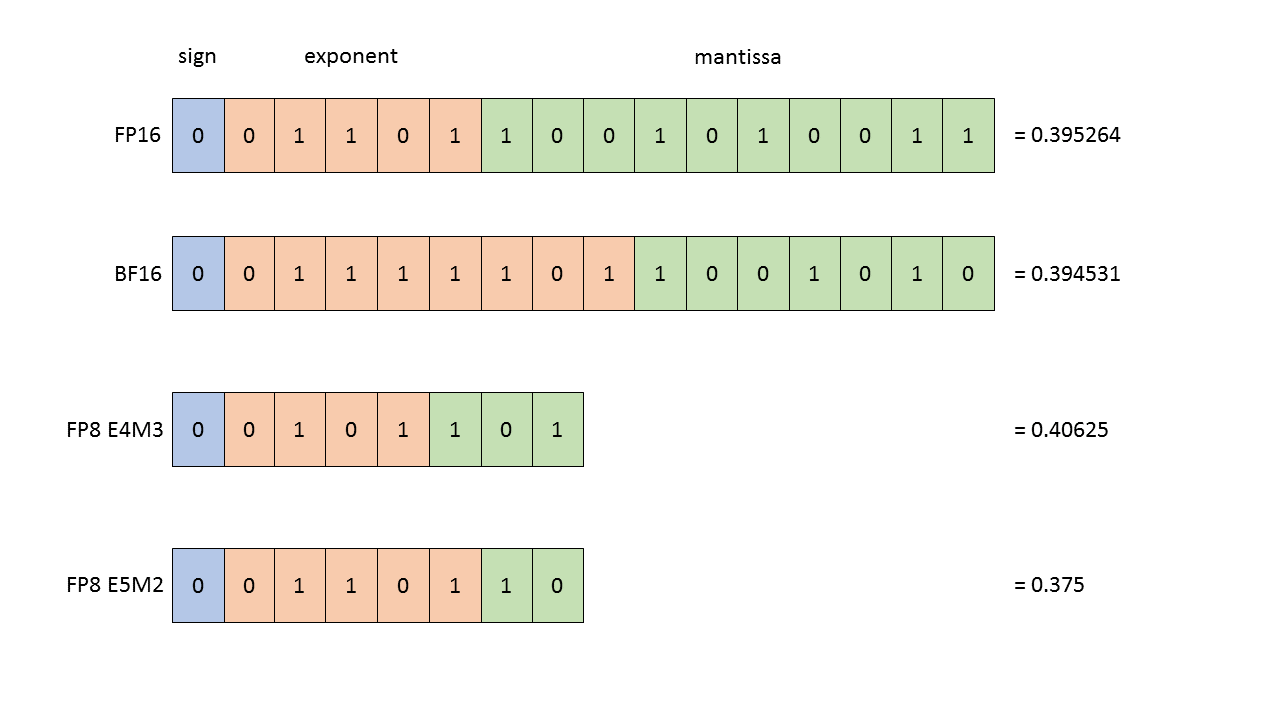
如图,
NVIDIA H100 GPU 原生支持两种 FP8(8-bit floating point) 编码格式:
| 格式 | 名称含义 | 指数位 (E) | 尾数位 (M) | 数值范围 |
|---|---|---|---|---|
| E4M3 | 4 位指数,3 位尾数 | 4 | 3 | [-448, 448] |
| E5M2 | 5 位指数,2 位尾数 | 5 | 2 | [-57,344, 57,344] |
E4M3 与 E5M2 的差异
-
E4M3:精度更高、范围更小 适合用于 权重(weights)、激活值(activations) 等数值分布稳定的张量。 因为尾数位更多,可以保留更高的计算精度。
-
E5M2:范围更大、精度更低 适合用于 梯度(gradients) 或中间变量,防止反向传播时数值溢出。
Transformer Engine 中的 FP8 使用策略
NVIDIA 提供的 Transformer Engine (TE) 框架中,对不同类型的张量有明确的 FP8 使用建议:
| 张量类型 | 推荐精度 | 理由 |
|---|---|---|
| 激活值 (activations) | FP8 (E4M3) | 分布集中,范围较小,节省显存 |
| 权重 (weights) | FP8 (E4M3) | 模型参数稳定,精度要求高 |
| 梯度 (gradients) | FP8 (E5M2) | 范围大、波动大,E5M2 范围更广 |
| 权重主副本 (master weights) | FP16 / BF16 / FP32 | 保证收敛与稳定性 |
| 优化器状态 (optimizer states) | FP32 | 累积误差敏感,需要高精度 |
前向与反向计算流程
下面是 Transformer Engine 的 FP8 混合精度计算流程:
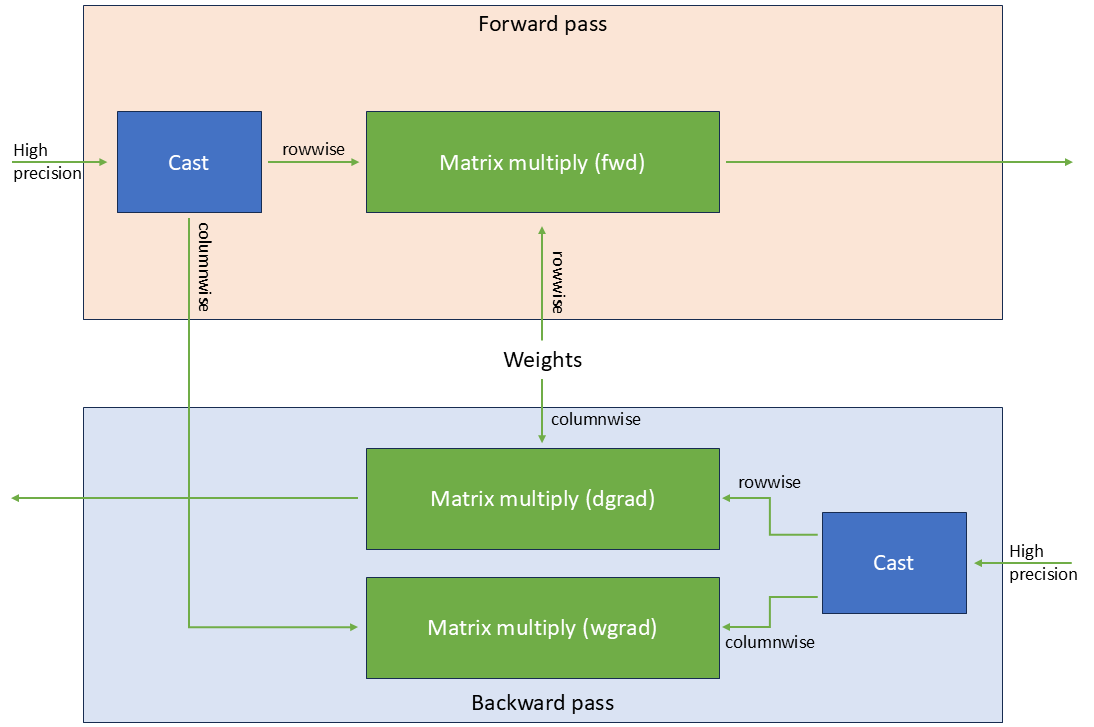
Forward:
input(fp8, e4m3) × weight(fp8, e4m3) -> output(fp8, e4m3)
output(fp8) -> convert(fp16/bf16) for next layer
Backward:
gradients(fp8, e5m2) -> accumulate(fp16/bf16)
master weights(fp32) -> update -> re-quantize(fp8)
关键思想
-
低精度参与矩阵乘法: 节省显存与带宽,加速训练。
-
高精度保存模型状态: 用于反向传播与优化器更新,保证数值稳定与可收敛性。
也就是说:
- 计算阶段使用 FP8(提升吞吐);
- 状态保存阶段使用 FP16/BF16/FP32(保证精度);
- 通过动态量化(Dynamic Scaling)策略避免溢出。
参考
- NVIDIA 官方文档:FP8 Primer
- 论文:FP8 Formats for Deep Learning