1. 为什么必须并行:瓶颈来自两类量
1.1 计算限制(Compute bound)
单卡算力有限;更关键的是训练吞吐不仅看 FLOPs,还看通信能否被掩盖(overlap)以及并行策略的同步频率(每层同步 vs 每步同步)。
1.2 显存限制(Memory bound)
显存消耗大体分三块:
1) 模型状态(model states):参数、梯度、优化器状态。
2) 激活(activations):为了反向传播需要保留的中间张量。
3) 临时张量/缓存(workspace / buffers):GEMM、通信 buffer、KV cache(推理/长上下文训练更明显)。
很多只看 1),但长序列/深层模型的 2) 往往更致命:哪怕 ZeRO-3 把模型状态切到很省,激活仍可能把你 OOM。
2. 统一记号公式
为了让后面的推导能直接对齐公式,这里固定一套符号:
| 符号 | 含义 |
| $s$ | sequence length(序列长度) |
| $b$ | micro-batch size(单卡微批大小,注意不是全局 batch) |
| $B$ | global batch size(全局 batch) |
| $h$ | hidden size(隐藏维度) |
| $a$ | attention heads(注意力头数) |
| $F$ | FFN 维度(通常 $\approx 4h$,但不同架构会变) |
| $X$ | 数据并行度(DP/FSDP 的分片数) |
| $t$ | 张量并行度(TP 的并行度) |
| $p$ | 流水线段数(PP 的 stage 数) |
| $m$ | micro-batch 数(用于 PP 填气泡的分块数) |
下面所有“显存公式”默认按“元素个数”计,再乘以 dtype 字节数(fp16/bf16 是 2 bytes,fp32 是 4 bytes)。
激活公式把 dtype 常数吸收到系数里了,我们沿用它的写法。
3. 模型状态显存:DDP 与 ZeRO 1-3 的一眼对比
设模型参数量为 $P$(参数元素总数)。对 Adam 类优化器,常见会有两份一阶/二阶动量($m,v$),再加上梯度与参数本身。忽略“fp32 master weights”等工程细节,用最常用的抽象:
- 参数:$P$
- 梯度:$P$
- Adam 状态:$2P$
因此,朴素 DDP(每卡复制一份)的模型状态元素数近似: \(M_{\text{DDP}} \approx P + P + 2P = 4P\)
ZeRO 的核心就是:把这些状态沿着数据并行维度 $X$ 分片(partition)。
3.1 ZeRO-1/2/3:每级到底省了什么
| 方法 | 每卡参数 | 每卡梯度 | 每卡优化器状态 | 合计(元素数) |
| : | : | : | : | : |
| DDP | $P$ | $P$ | $2P$ | $4P$ |
| ZeRO-1 | $P$ | $P$ | $\frac{2P}{X}$ | $2P + \frac{2P}{X}$ |
| ZeRO-2 | $P$ | $\frac{P}{X}$ | $\frac{2P}{X}$ | $P + \frac{3P}{X}$ |
| ZeRO-3(FSDP) | $\frac{P}{X}$ | $\frac{P}{X}$ | $\frac{2P}{X}$ | $\frac{4P}{X}$ |
3.2 把“元素数”换算成字节:一个常用的心算模板
上表只数了“元素个数”,实际显存要乘以 dtype 字节数。以一个常见工程配置为例(不是唯一实现,只是最常见的量级):
- 参数(bf16/fp16):2 bytes
- 梯度(bf16/fp16):2 bytes
- Adam $m,v$(fp32):$4+4=8$ bytes
则每个参数对应的模型状态约为 $2+2+8=12$ bytes(如果你还保留 fp32 master weights,再额外 +4 bytes)。
因此 DDP 粗略可以心算为“每个参数 12 bytes(或 16 bytes)”,ZeRO-3 则近似再除以 $X$。
3.3 但 ZeRO-3 并不“免费”:通信模式变了
- DDP:每步(backward 末尾)对梯度做一次 All-Reduce。
- ZeRO-3:在 forward/backward 的每个 layer,都会触发参数的 All-Gather / Reduce-Scatter(实现不同略有差异,但核心结论是:通信更细粒度、更频繁)。
因此当 batch 很小、单步计算很短时,ZeRO-3 的“固定通信开销”更难被掩盖(这会在后文的 Batch-size scaling 里体现为一条随 $B$ 变好的曲线)。
4. ZeRO-3 vs 模型并行:都“切参数”,但运行时逻辑完全不同
从静态存储上看,ZeRO-3 和模型并行都可以“把参数切碎散落到多卡上”,所以经常被混淆。但训练运行时的数据移动对象不同:
-
ZeRO-3:权重在动,激活不动(按层拉权重)
计算第 $l$ 层时,把第 $l$ 层权重 All-Gather 到本卡,算完就释放/换下一层;激活在本卡保持(尤其长序列时仍很大)。 -
模型并行(TP/PP/CP…):权重相对静态,激活在动(按算子/按层传激活)
每卡只持有自己那份分片权重/层段;为了完成一次前向/反向,需要频繁同步/传递激活或其分片。
5. 模型并行两大件:TP(张量并行)与 PP(流水并行)
5.1 张量并行(Tensor Parallel, TP):没有气泡,但每层都要同步
把一个大矩阵乘法(例如 $XW$)沿某个维度切开,让多张 GPU 同时参与一次 GEMM。优点是“没有气泡”(所有卡同时算),而且即使 batch 很小也能利用多卡。
但代价是:Transformer 每层都有多处需要聚合结果的点,因此 TP 往往伴随 All-Reduce / All-Gather。
经验公式(单层、forward+backward,总通信量的量级): \(\text{Comms}_{\text{TP}} \approx 8 \cdot b \cdot s \cdot h \cdot \left(\frac{t-1}{t}\right)\)
这个“8”来自两层含义叠加:
1) 一层里 forward 需要 2 次同步(Attention 后一次、MLP 后一次),backward 同样 2 次,共 4 次;
2) All-Reduce 本质上是“发数据 + 收数据”,等价数据量再乘 2;
所以 $4 \times 2 = 8$,并且每层都来一遍:层数越多,同步次数越多,网络越吃紧。
这也解释了为什么工程上通常要求:TP 尽量锁在单机内(NVLink/NVSwitch),不要跨机做 TP。
5.2 流水并行(Pipeline Parallel, PP):通信小,但有气泡
PP 是按层切:把 Layer 1~L 切成 $p$ 个 stage,每个 stage 一段连续层。相邻 stage 之间只需要点对点传激活: \(\text{Comms}_{\text{PP}} \sim b \cdot s \cdot h\)
PP 的问题是气泡(bubble):如果你只有 1 个 micro-batch,后面的 stage 必须等前面的 stage 先跑完一部分才有活干。
经典结论(1F1B 或类似 schedule 下的粗略估计):用 $m$ 个 micro-batch 去填充 $p$ 个 stage 时,气泡占比近似 \(\text{Bubble fraction} \approx \frac{p-1}{m}\)
这条公式非常实用:
- $p$ 越大(模型越大、流水线切得越细),越需要更大的 $m$ 来填满;
- 这也是为什么 PP 往往“逼你开大 batch / 用 gradient accumulation”。
6. 激活显存:最重要的推导
一个非常好用的近似,是把每层训练时需要保存的激活写成 \(\text{Activations memory per layer} = sbh \left( 34 + 5\frac{as}{h} \right)\)
它把激活拆成两部分:
- $34sbh$:与 $s$ 线性相关的激活(Linear term)
- $sbh \cdot 5\frac{as}{h} = 5bas^2$:Attention 带来的 二次项(Quadratic term)
6.1 为什么 Attention 会出现 $s^2$:从张量形状直接推
对自注意力来说,最占显存的中间物之一是注意力分数矩阵(以及 Softmax 后的概率、dropout mask 等)。它们的核心形状都是: \((\text{batch},\ \text{heads},\ s,\ s) = (b,\ a,\ s,\ s)\)
仅一个这样的矩阵,元素数就是 $b \cdot a \cdot s^2$。训练时为了反向传播,通常还要保留若干个同形状/同量级的中间量(scores、probs、mask、以及用于反传的缓存等),课程把这些合并成一个经验系数 “5”,于是得到: \(M_{\text{attn}} \approx 5 \cdot b \cdot a \cdot s^2\)
把它写成统一的 $sbh(\cdot)$ 形式,只是把 $b a s^2$ 用 $sbh$ 抽出公共因子: \(5bas^2 = sbh \cdot 5\frac{as}{h}\)
这一步很关键:它让你一眼看出这项随 $s$ 二次增长,也是长上下文训练最容易炸显存的根源。
6.2.1 代入一个长上下文例子:为什么没有 FlashAttention 根本不可能
取一个很常见的量级:$b=1$、$a=32$、$s=32768$(32k)。二次项对应的元素数大约是: \(5bas^2 = 5 \cdot 1 \cdot 32 \cdot 32768^2 \approx 1.7\times 10^{11}\ \text{elements}\)
哪怕这些元素都用 bf16(2 bytes)存储,也约是 $3.4\times 10^{11}$ bytes $\approx 343$ GB——这还只是“一层里那几个 $(b,a,s,s)$ 级别中间量”的量级,显然单卡(甚至单机)都放不下。
所以长上下文训练几乎默认需要 FlashAttention/重算把 $s^2$ 项拿掉,否则连讨论并行都没有意义。
6.2 那个 “34” 是什么:线性项的本质是“每个 token 需要保留多少个 $h$ 向量”
线性项写成 $34sbh$ 的意思是:对每个 token(总数 $b\cdot s$),训练一层大约要保留 $O(10\sim 100)$ 个“长度为 $h$ 的向量”(以及若干同量级的中间缓冲),常数近似为 34。它来自:
- Attention 模块里的 Q/K/V、投影前后的张量、残差分支;
- MLP 模块里的升/降维投影的输入输出、激活函数中间量;
- LayerNorm / Dropout 相关输入输出(这部分在并行化时会变得“顽固”,下一节会专门讲)。
这类张量的共同点是:它们形状都近似 $(b,s,h)$,因此元素数和显存都与 $sbh$ 成正比。
你不必把 34 当作“永恒真理”,它依赖具体实现和是否重计算,但它在“估算趋势/对比策略”上非常好用。
7. 让激活显存随并行度线性缩放:TP、FlashAttention、SP、CP 各干掉哪一项
7.1 TP 之后为什么会出现“剩余的 10”
课程给出的 TP 版本激活公式是: \(\text{Activations} = sbh \left( 10 + \frac{24}{t} + 5\frac{as}{ht} \right)\)
它等价于把上一节的 $34$ 拆成两块: \(34 = 10 + 24\)
并且断言:
- 那些“跟 GEMM/权重分片对齐”的线性激活,能随 TP 并行度按 $\frac{1}{t}$ 缩放(所以变成 $\frac{24}{t}$);
- Attention 的 $s^2$ 项,在 TP 下相当于把 head 维度切分,因此也按 $\frac{1}{t}$ 缩放(所以从 $5\frac{as}{h}$ 变成 $5\frac{as}{ht}$);
- 但 LayerNorm / Dropout / 残差入口等位置需要“完整的 $h$ 维向量”才能计算,TP 会在这些点上做 All-Reduce 聚合出完整向量,因此对应的激活 不能被切分,就留下了一个不随 $t$ 下降的常数项 “10”。
这解释了一个很反直觉的现象:TP 越大,理论上越省,但最终会被那块不下降的 “10sbh” 卡住。
7.2 FlashAttention / selective activation recomputation:把 $s^2$ 直接打没
FlashAttention 的核心是:不显式存下 $(b,a,s,s)$ 的 attention 矩阵(以及相关概率矩阵),而是在反向传播时对必要的部分进行重算(recompute),将显存从 $O(s^2)$ 降为接近 $O(s)$。
在课程的近似写法里,这等价于把二次项近似视为 0: \(5\frac{as}{h}\ \approx\ 0\)
于是 TP + selective recomputation 时: \(\text{Activations} \approx sbh \left( 10 + \frac{24}{t} \right)\)
注意:它并没有让线性项消失,只是把最危险的 $s^2$ 项移走了,所以长序列时“救命”,但并行度很大时仍可能被“10”卡住。
7.3 Sequence Parallel(SP):不增加通信量,干掉顽固的 “10”
SP 的直觉是:既然 TP 在某些点必须 All-Reduce 才能拿到完整向量,那我们把这个 All-Reduce 拆开:
- 原本的 All-Reduce(得到完整向量)
- 改成 Reduce-Scatter(每卡只拿到自己那一片向量)→ 在分片上做 LayerNorm/Dropout → All-Gather(进入下一个需要完整输入的地方)
Reduce-Scatter + All-Gather 的字节数与 All-Reduce 等价,所以课程强调:SP 不增加通信量,却能把原本不能切分的那块线性激活也按 $\frac{1}{t}$ 切掉。
因此 TP + SP 的激活公式变为: \(\text{Activations} = sbh \left( \frac{34}{t} + 5\frac{as}{ht} \right)\)
如果再叠加 FlashAttention(去掉 $s^2$ 项),就得到理想状态: \(\text{Activations} \approx sbh \left( \frac{34}{t} \right)\)
也就是“激活随并行度线性缩放”。
7.4 Context Parallel / Ulysses:把“切 head”换成“切序列”,为超长上下文而生
当 $s$ 非常大时,你关心的不再只是 attention 矩阵的中间量,还包括更多“与序列长度线性相关但常数很大”的东西(以及推理场景的 KV cache)。这时可以把切分维度从 head 改为 sequence:
- Linear/MLP(逐 token)阶段:保持“按序列切分”,每卡只算自己那段 token,不需要通信;
- 进入 Attention:用两次 All-to-All 做一次“分布式转置”,让每卡临时拥有“完整序列的一部分 head”,以便完成注意力计算;
- 出 Attention:再 All-to-All 转回“按序列切分”。
它的本质是把“长序列难题”转化成“多头并行/通信转置难题”,因此对拓扑更敏感,但在 long context 场景往往是必须的。
7.5 一张表总结:每种技术到底把哪一项除掉
| Configuration | Activations Memory Per Transformer Layer |
| no parallelism | $sbh (34 + 5 \frac{as}{h})$ |
| tensor parallel (baseline) | $sbh (10 + \frac{24}{t} + 5 \frac{as}{ht})$ |
| tensor + sequence parallel | $sbh (\frac{34}{t} + 5 \frac{as}{ht})$ |
| tensor parallel + selective activation recomputation | $sbh (10 + \frac{24}{t})$ |
| tensor parallel + sequence parallel + selective activation recomputation | $sbh (\frac{34}{t})$ |
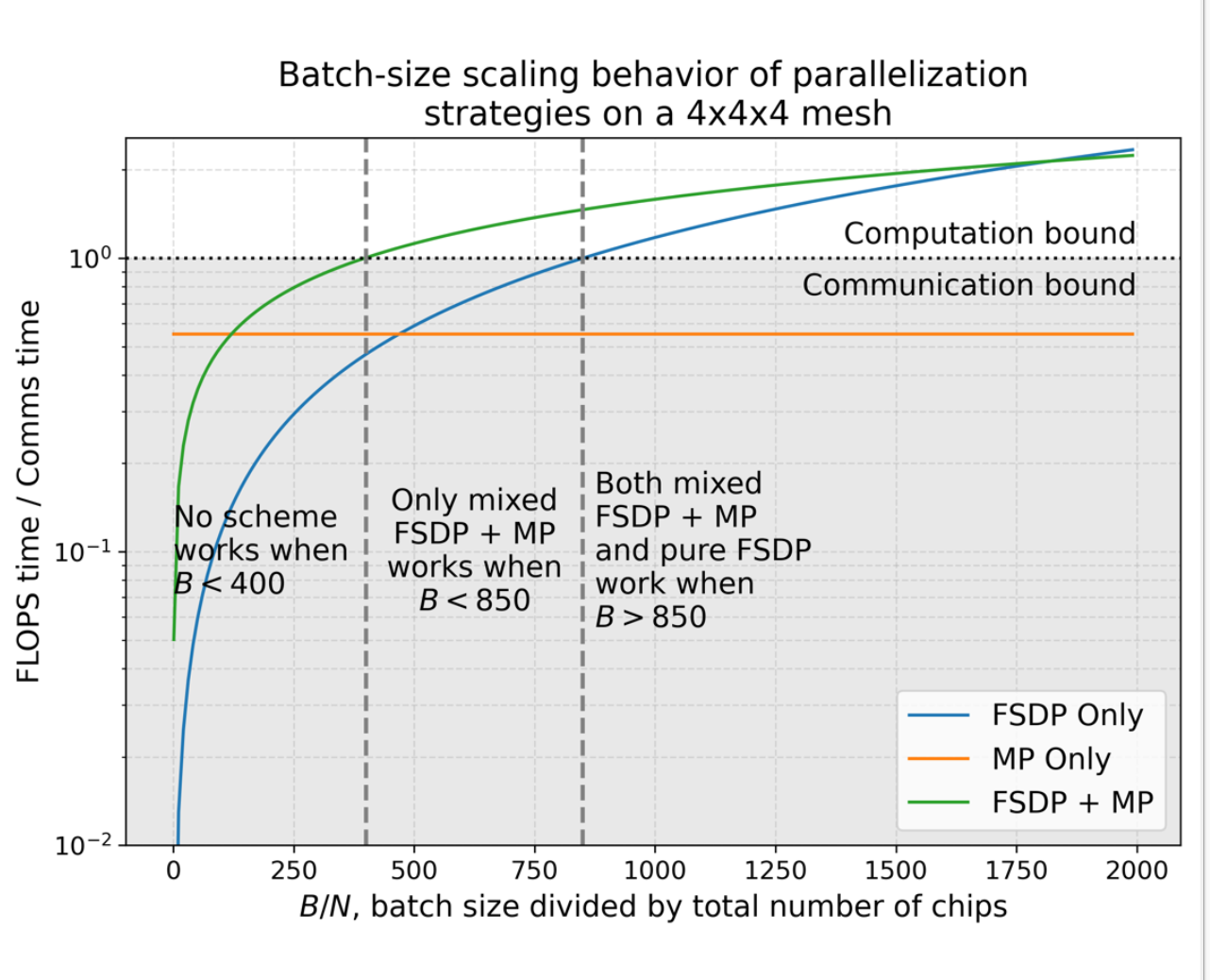
8. Batch size scaling:为什么小 batch 更偏向 MP,大 batch 更偏向 FSDP
这个图本质在讲:不同并行策略的“通信项”到底随不随 $B$ 变化。
8.1 一层计算量从哪来:$4BDF$ 与 $8BDF$ 的含义
把一层里最主要的 GEMM 抽象成矩阵乘法(忽略 MoE gating 等细节):
- forward 的主成本:若干个 $D \leftrightarrow F$ 的线性层。对一个 $D\to F$ 的线性层,token 数量级是 $B$(这里 $B$ 表示每卡看到的 token 数/样本数的合并量,课程符号沿用即可),一次 GEMM 的 FLOPs 近似 $2BDF$。
- 一个 Transformer 层里大致有两次这种量级的 GEMM(例如 FFN 的 up/down),于是 forward 近似 $4BDF$;
- backward 通常约为 forward 的 2 倍,因此写成 $8BDF$。
这就是表里 “Compute per layer = 4BDF + 8BDF” 的来源。
8.2 通信量:FSDP 固定开销,MP 与 batch 成正比
并行策略的计算/通信模型(课程表格):
| Strategy | Compute per layer (ignoring gating einsum) |
Comms per layer (bytes, forward + backward pass) |
| DP | $\frac{4BDF}{X} + \frac{8BDF}{X}$ | $0 + 8DF$ |
| FSDP | $\frac{4BDF}{X} + \frac{8BDF}{X}$ | $4DF + 8DF$ |
| MP | $\frac{4BDF}{Y} + \frac{8BDF}{Y}$ | $4BD + 4BD$ |
| FSDP + MP | $\frac{4BDF}{XY} + \frac{8BDF}{XY}$ | $(\frac{4BD}{X} + \frac{4DF}{Y}) + (\frac{8BD}{X} + \frac{8DF}{Y})$ |
符号:$D$ 为 hidden size,$F$ 为 FFN size,$X$ 为数据并行度(或 FSDP 分片数),$Y$ 为模型并行度(这里用来表示 MP 的切分数)。
从这张表你应该记住两句话:
1) FSDP 的通信里有大量 $DF$ 项:它与模型大小相关,跟 $B$ 无关,因此对小 batch 是固定负担。
2) MP 的通信里是 $BD$ 项:它传的是激活/中间结果,因此随 batch 线性增长;分子分母都线性增长,所以在图上表现为“几乎一条平线”。
这就得到工程建议(课程图里的三个区间):
- $B$ 太小:谁都跑不满,需要梯度累积(增加有效 batch)
- 中等 $B$:混合(FSDP + MP)更稳
- 足够大 $B$:FSDP 往往足够好、实现也更简单
9. 3D 并行与网络拓扑:为什么常见顺序是“机内 TP,机间 PP,最外层 DP/FSDP”
课程(Narayanan 2021)的经验法则可以总结为一句话:
把“最怕延迟、最频繁同步”的并行放到带宽最高的层级。
因此一个常见排序是:TP(机内)→ PP/CP(跨机但通信量较可控)→ DP/FSDP(最外层,可 overlap、容忍延迟)。
工程落地时通常按以下步骤扩展:
1) 先把 TP 拉到单机满配(例如 8 卡 HGX/H100);
2) 模型再大就用 PP 跨机切层,尽量不要跨机做 TP;
3) 剩余卡数用 DP/FSDP 提吞吐。
10. 重计算(Activation Recomputation):为什么“多算 33%”可能反而更快
课程的 Slide 53 给了一个很务实的结论:重计算省下的显存,往往能换来更大的 batch / 更多 micro-batch,从而显著减少 PP 的气泡,让整体吞吐提升。
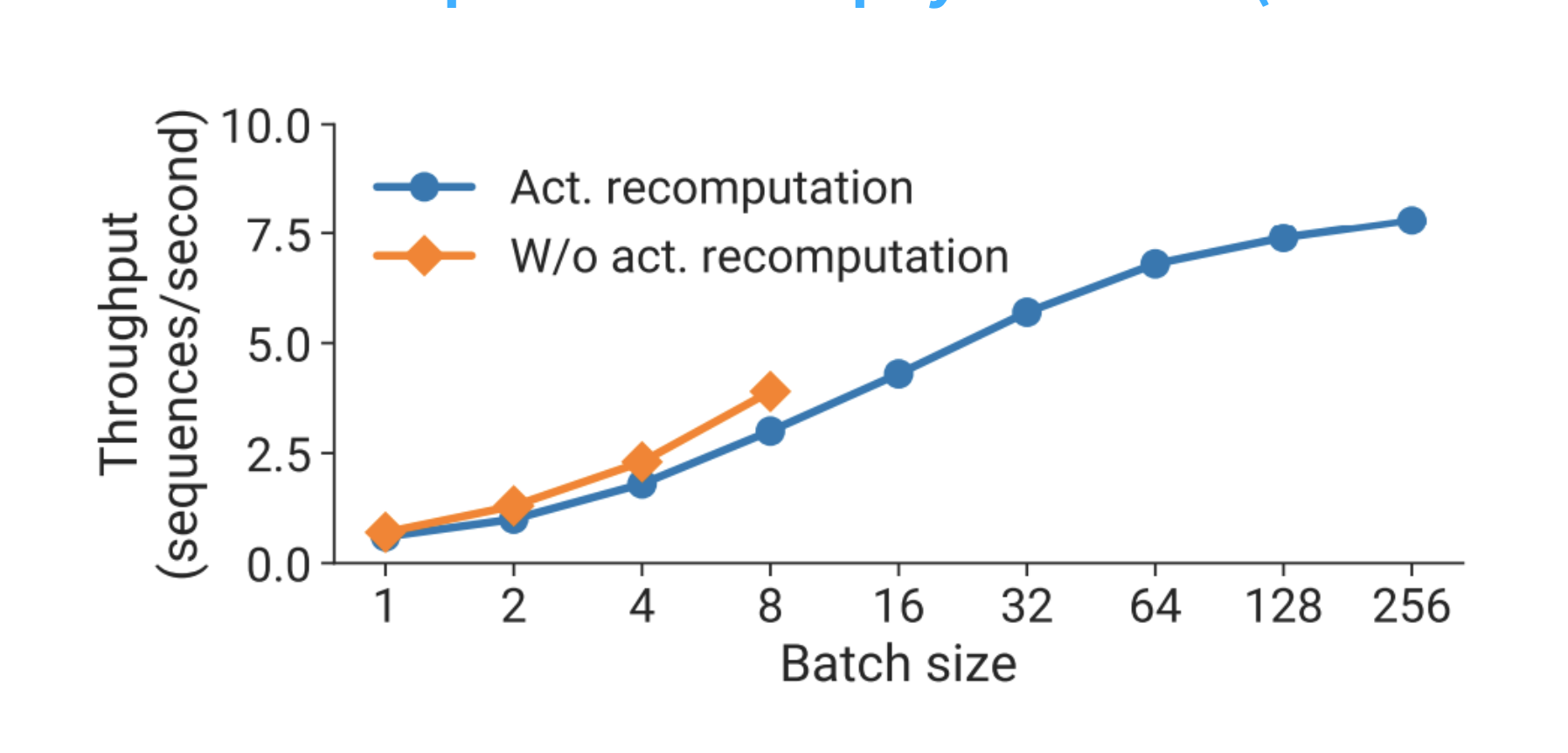
把链条写成公式语言就是:
- 开重算:单步计算时间 $\uparrow$(多做一些 forward)
- 但激活显存 $\downarrow$:能把 $m$(micro-batch 数)开大
- 气泡占比 $\frac{p-1}{m}\downarrow$:PP 利用率上升
- 最终吞吐可能 $\uparrow$:尤其当你本来被 bubble 卡住时
11. 近期大模型并行配置速览(对照前文公式理解“为什么”)
- Dolma 7B:以 FSDP 为主。
- DeepSeek:ZeRO-1 + Tensor/Sequence/Pipeline 并行;V3 使用 PP=16、EP 64-way(8 nodes)、ZeRO-1。
- Yi / Yi-lightning:ZeRO-1 + Tensor + Pipeline;Lightning 用 Expert Parallel 替代 Tensor。
- Llama 3 405B:并行层级顺序 $[TP, CP, PP, DP]$;TP=8 锁在机内;长序列阶段引入 CP=16,DP 下降以腾出资源。
- Gemma 2 (2/9/27B):ZeRO-3 + MP(常指 TP+SP)+ DP。
12. 结论速记(从公式出发)
- 模型状态显存:ZeRO-3 让模型状态近似按 $\frac{1}{X}$ 缩放,但它不解决激活。
- 激活显存:长序列的 $s^2$ 项必须靠 FlashAttention/重算去掉;大 TP 下顽固项 “10” 需要 SP 才能线性缩放。
- 选型直觉:小 batch 更怕“固定通信开销”→ 更偏 MP;大 batch 更容易掩盖固定通信 → FSDP 更香。
- 拓扑原则:机内带宽最高 → TP 放机内;跨机更怕 All-Reduce → 用 PP/CP;最外层用 DP/FSDP。