Scaling Law

layout: article title: Scaling Laws：从幂律到 Chinchilla（以及训练配方） tags: LLM ScalingLaw

旧方法：在大模型上直接调参（极度昂贵且缓慢）。
新方法（Scaling Laws）：在小模型上调参，总结规律，然后外推（extrapolate）到大模型。

TL;DR

大模型的很多宏观规律在 log-log 图上近似直线：Loss ≈ A · x^{-α}。
数据“质量/构成”主要影响 截距（offset），规模带来的收益速率（斜率 slope）往往更稳定。
数据会“用完”：重复数据（多 epoch）会带来收益递减，需要用“有效数据量”修正。
规模（scale）通常压倒形状（shape）：不少结构超参在很宽范围内影响很小。
对固定算力预算，最关键的问题不是“能不能训大”，而是“模型大小 N 与数据量 D 怎么配”；Kaplan 的建议后来被 Chinchilla 修正为更接近 N:D ≈ 1:1 的增长策略。

1. Scaling law 是什么：为什么 `log-log` 上是一条直线？

幂律（Power law）的核心形式：

\[\text{Loss} \approx A \cdot x^{-\alpha} + \text{(常数/下界)}\]

为简洁起见，本文把测试集上的 loss / error（如 test loss、generalization error）统称为 “Loss/误差”，不区分具体任务指标的常数差异。

在双对数坐标系中：

\[\log(\text{Loss}) \approx -\alpha \log(x) + \log(A)\]

所以看起来像“直线”。这件事非常重要：一旦“直线性”成立，很多“炼丹经验”就能变成可拟合、可外推、可做预算的工程规律。

2. 简史：从早期观察到 LLM 时代“物理定律”

1993/2001：已有关于数据规模与性能关系的早期讨论。
Hestness et al. 2017：深度学习时代 scaling law 重要先驱，提出“计算受限 / 数据受限”等概念，并用学习曲线解释不同阶段的行为。
Kaplan et al. 2020（OpenAI）：把 LLM 的 scaling law 系统化，给出算力/数据/参数与 loss 的稳定幂律关系。
Hoffman et al. 2022（DeepMind, Chinchilla）：在“固定算力预算”场景下重新推导/拟合，指出当时很多大模型（包括 GPT-3）在配比上“虚胖”，应使用更小模型+更多数据。

3. Kaplan 2020：三大要素的幂律关系（Compute / Data / Params）

这张图几乎奠定了 scaling laws 在大模型里的“工程学地位”：

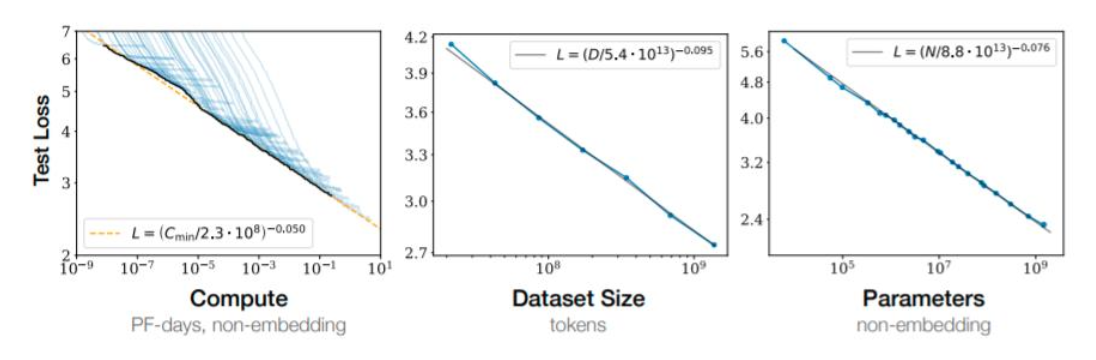
Kaplan 2020：Loss 与 compute/data/params 的幂律

在合适的训练设置下，测试集 loss 与三类资源满足稳定幂律（指数来自课堂材料）：

算力（Compute, $C$）
- 结论：算力越多，能达到的最优 loss 越低（包络线/envelope）。
- 经验形式：$L \propto C^{-0.050}$。
数据量（Dataset size, $D$）
- 前提：模型足够大，不是瓶颈。
- 经验形式：$L \propto D^{-0.095}$。
参数量（Parameters, $N$）
- 前提：数据足够多，不是瓶颈。
- 经验形式：$L \propto N^{-0.076}$（常见口径：不计 embedding）。

3.1 关键观察：跨分布时“平行线”

Kaplan 还强调了一个对泛化很关键的现象：即使训练分布与测试分布不同（train ≠ test），缩放趋势仍基本成立，差异多体现为截距变化而非斜率变化。

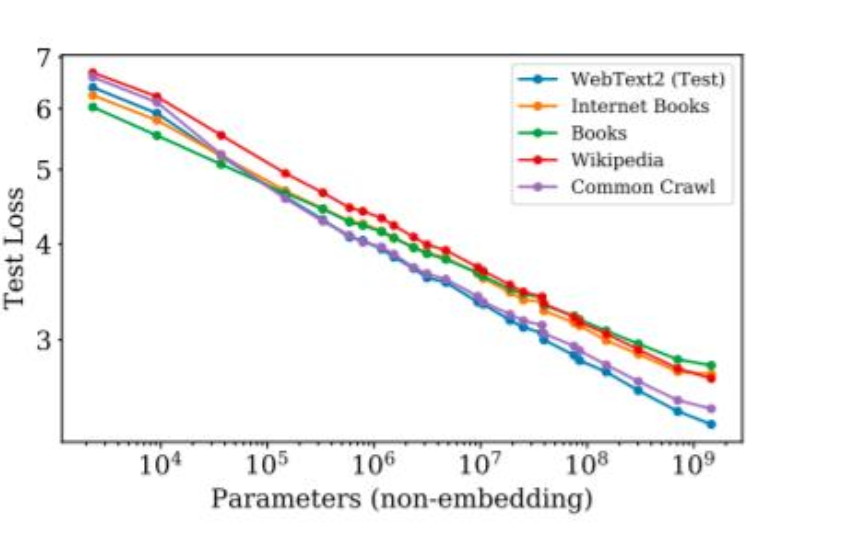
跨测试集：平行线与 offset

直觉：换一个更难的测试域，相当于整条线整体上移（更高 loss），但“变大带来的收益速率”相近。

4. 数据缩放：三阶段学习曲线（以及为什么斜率看起来很慢）

4.1 更完整的视角：不是永远幂律，而是“三阶段”

Hestness 2017 的学习曲线常被概括为类似 Logistic 的三阶段（在 log-log 下的形态）：

小数据区（Small data）：几乎学不到规律，像“瞎猜”，曲线平。
幂律区（Power-law）：双对数下近似直线，这是我们最关心的区域。
不可约误差区（Irreducible error）：受噪声、任务不确定性、Bayes error/熵下界影响，曲线再次变平。

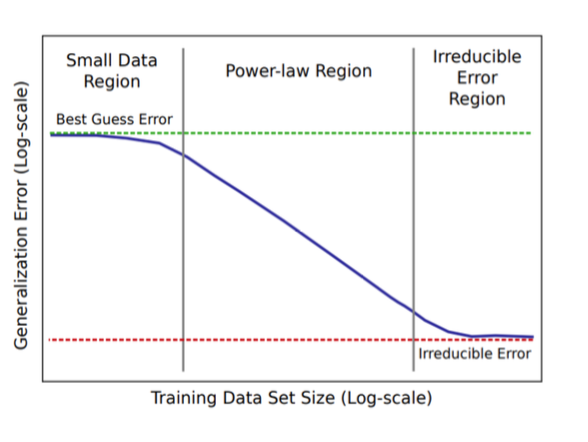
三阶段学习曲线

对于语言模型，幂律区经常表现得非常“直”：

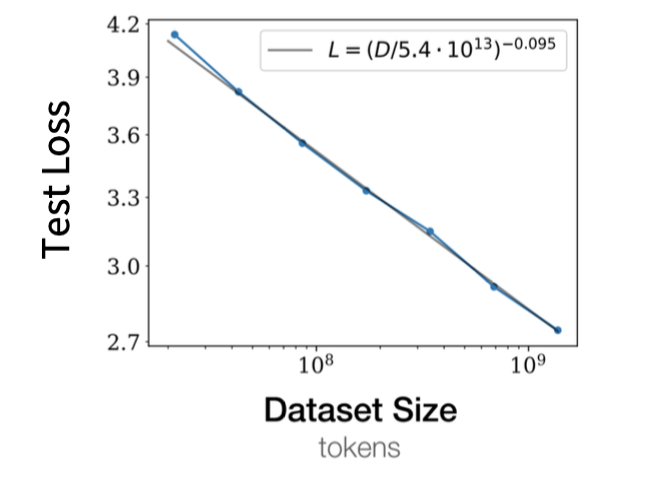
语言模型：data scaling 的线性区

4.2 一个最简单的推导：为什么会出现直线？

先看一个极简统计任务：从 $N(\mu,\sigma^2)$ 采样 $n$ 个点，用均值 $\hat{\mu}$ 估计 $\mu$。

均方误差： $E[(\hat{\mu}-\mu)^2]=\frac{\sigma^2}{n}$

两边取 log： $\log(\text{Error})=-\log(n)+2\log(\sigma)$

在 log-log 图上就是斜率为 -1 的直线。更一般地，任何 $1/n^\alpha$ 的多项式衰减都会呈现“缩放直线”。

从简单估计到幂律

4.3 为什么神经网络的幂律斜率很小？（维数灾难直觉）

对神经网络更像“非参数估计”：不是估计有限维参数，而是在高维空间里逼近函数。一个直观的“切方块（box method）”思路能给出：

在 $d$ 维空间中， $\text{Error} \propto n^{-1/d} \quad \Rightarrow \quad \log(\text{Error})=-\frac{1}{d}\log(n)+C$

所以：

有效维度 $d$ 越大，斜率 $-1/d$ 越接近 0（曲线越平，进步越慢）。
语言/视觉任务的内在维度往往很高，这会让 $\alpha$ 看起来“小得合理”。

Bahri et al. 2021 尝试用真实数据集验证“$\alpha \propto 1/d$”的趋势（但也提醒：内在维度估计本身并不牢靠）：

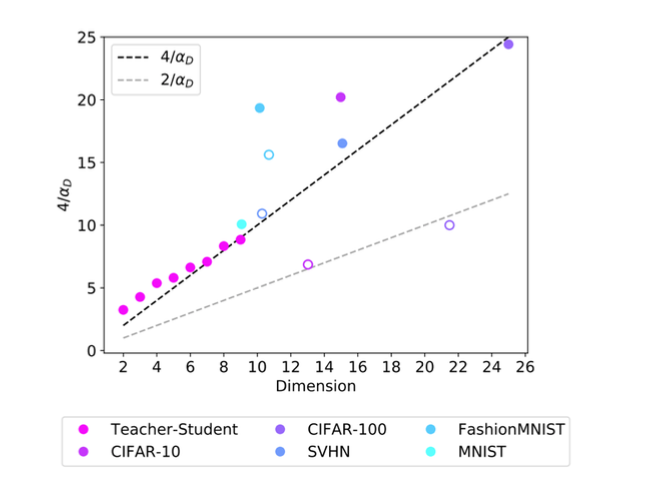
intrinsic dimension 与斜率关系

5. 数据“怎么选”比“堆多少”更早影响收益：质量、构成与分布偏移

5.1 金科玉律：数据构成影响 offset，不太影响 slope

Data composition affects the offset, not the slope.
（数据质量/构成主要改变截距，不显著改变斜率。）

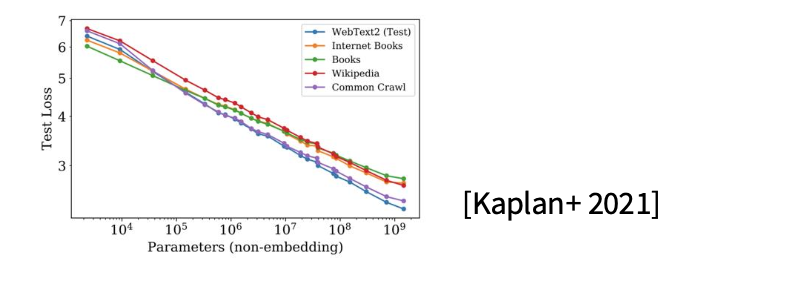
不同数据源：平行线

直觉类比：两个人跑步速度一样（斜率相同），但起跑线不同（截距不同）。高质量数据让你“从更靠前的地方起跑”。

5.2 分布偏移与混合数据：存在“最佳配比”

Hashimoto (2021) 讨论了训练/测试分布不一致时的情况：平行线依旧常见，但截距会因为分布不匹配而上移；混合多个数据源时，截距常呈现 U 型并存在最优点。

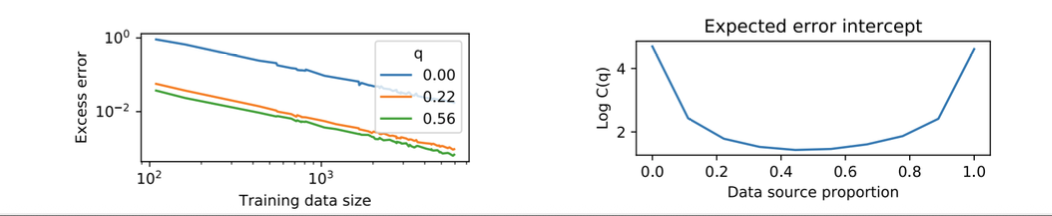
分布偏移与混合比例

工程启示

坏数据无法靠“扩大规模”高效弥补（斜率差不多，offset 太高会很亏）。
数据清洗/筛选相当于把整条曲线整体下移，是“便宜”的提升。
多样性很关键：适当混合数据源能降低分布偏移带来的截距惩罚。

6. 现实修正：数据有限时的重复训练与“有效数据量”

当高质量数据用完，被迫多 epoch 重复时，会出现明显的收益递减：

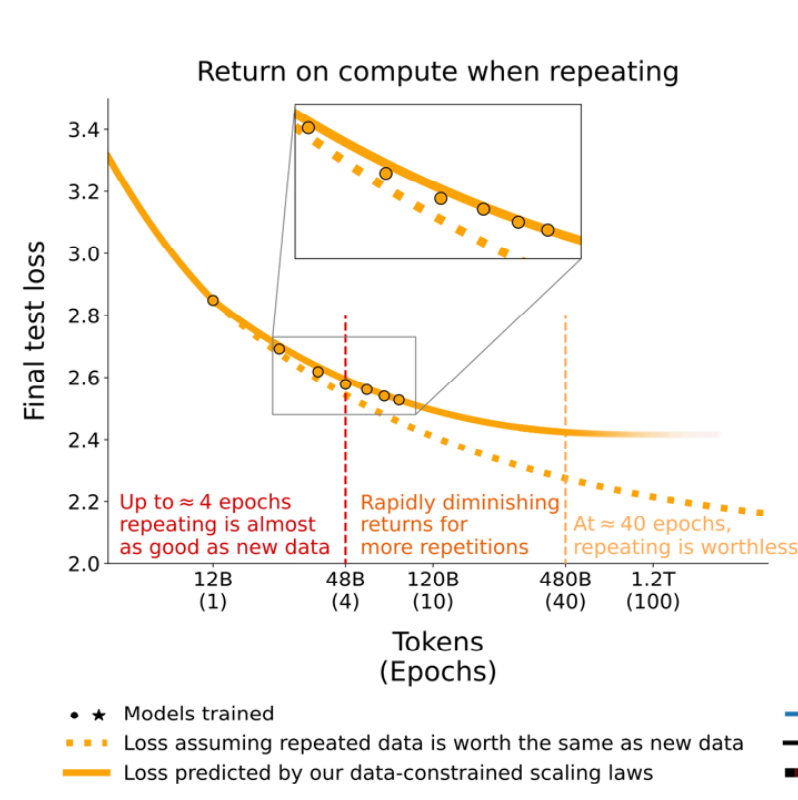
重复数据：收益递减

经验法则（课堂给出的口径）：

重复到约 4 epochs：效果接近“新数据”。
重复到约 40 epochs：几乎“worthless”，泛化收益很差。

6.1 用“有效数据量”修正

一种修正写法（指数饱和）：

\[D' = U_D + U_D R_D^* \left(1 - e^{-R_D / R_D^*}\right)\]

$D’$：有效数据量（模型“感觉”学到的量）。
$U_D$：唯一 token 数（原始数据规模）。
$R_D$：重复次数（epochs）。
$R_D^*$：饱和尺度（多大程度开始明显递减）。

6.2 数据受限时，算力怎么花？

在固定算力预算下，如果数据受限且必须重复，最优点会从“更小模型+更多 tokens”移动到“更大模型+更少 tokens”：

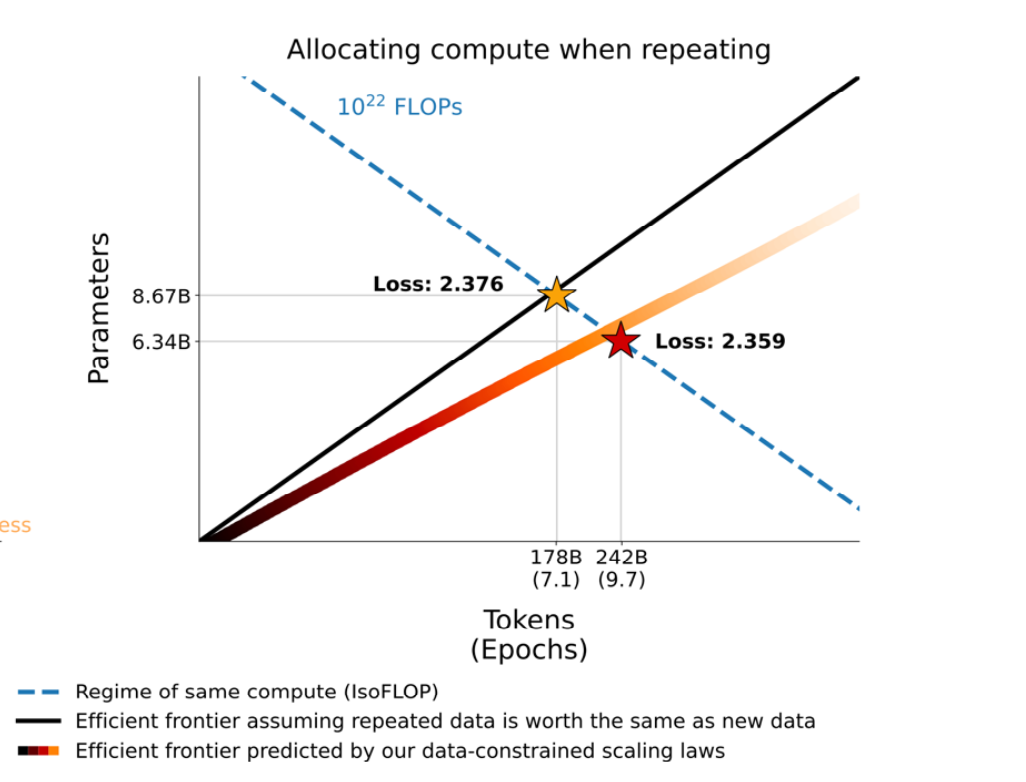
数据受限：最优点向更大模型移动

反直觉建议： 当数据不足（不得不大量重复）时，与其把模型训练更久，不如把模型做大一点。

7. 规模越大，筛选策略越不一样：动态数据池（Crossing curves）

一个非常实用的结论：数据筛选标准应随规模变化。小模型算力有限，能吃完高质量数据；大模型算力巨大，高质量数据不够用，过度筛选会迫使你重复数据，反而更亏。

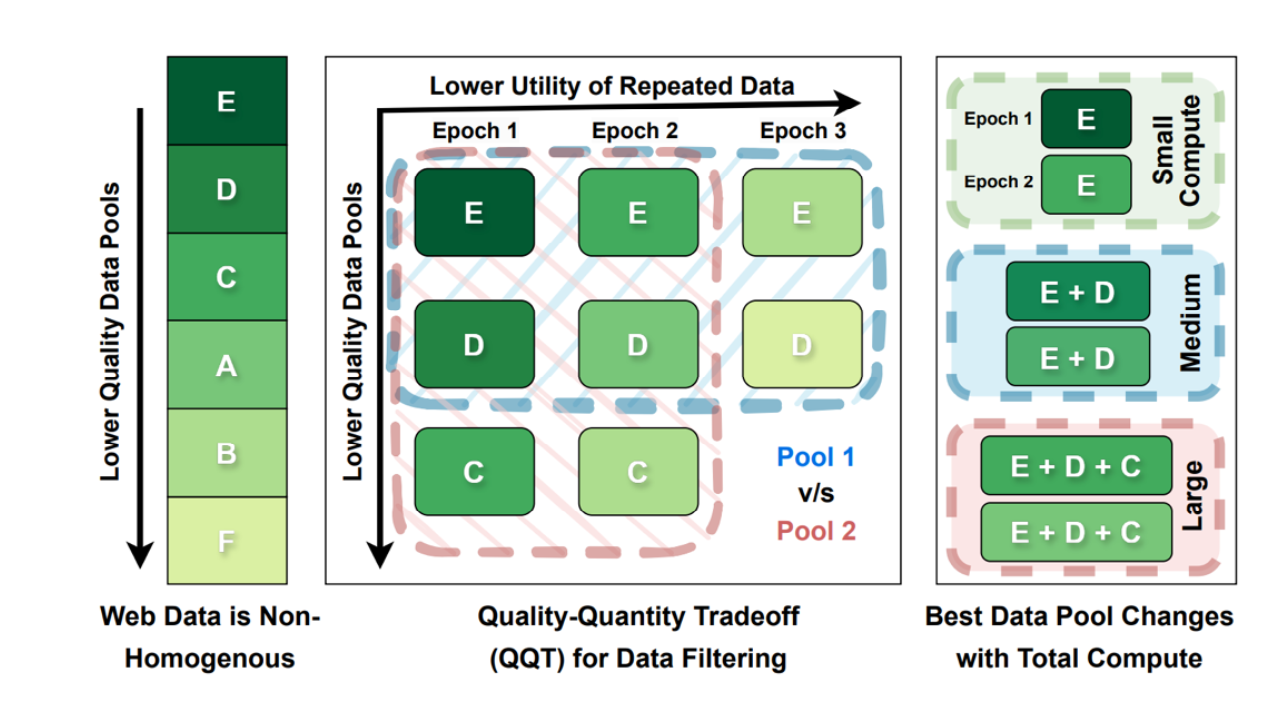
不同算力下的数据池策略

对应的“交叉曲线”现象：

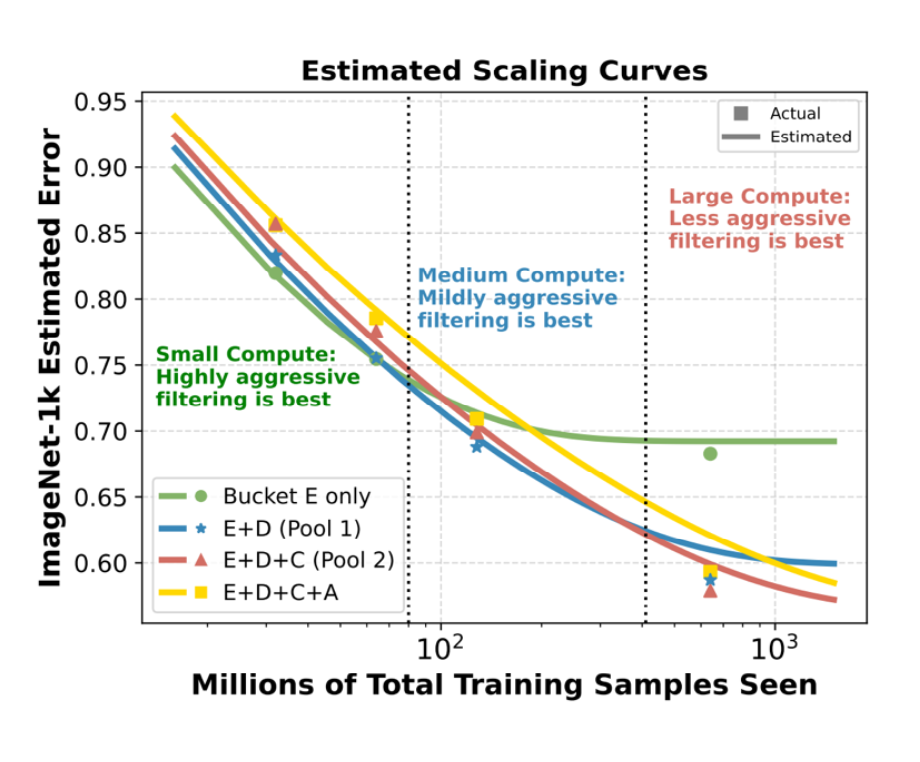
Crossing curves：小算力偏好纯净，大算力偏好多样

8. Scaling laws 给模型工程师的“答题卡”

这一部分把 scaling 的结论落到常见工程选择题上：架构、优化器、深度/宽度与参数口径、以及形状超参到底值不值。

8.1 架构：Transformer vs LSTM（大规模下差异会拉开）

Transformer vs LSTM

课堂结论：随着规模拉大，Transformer 往往能达到更低的 loss。

8.2 优化器：Adam vs SGD

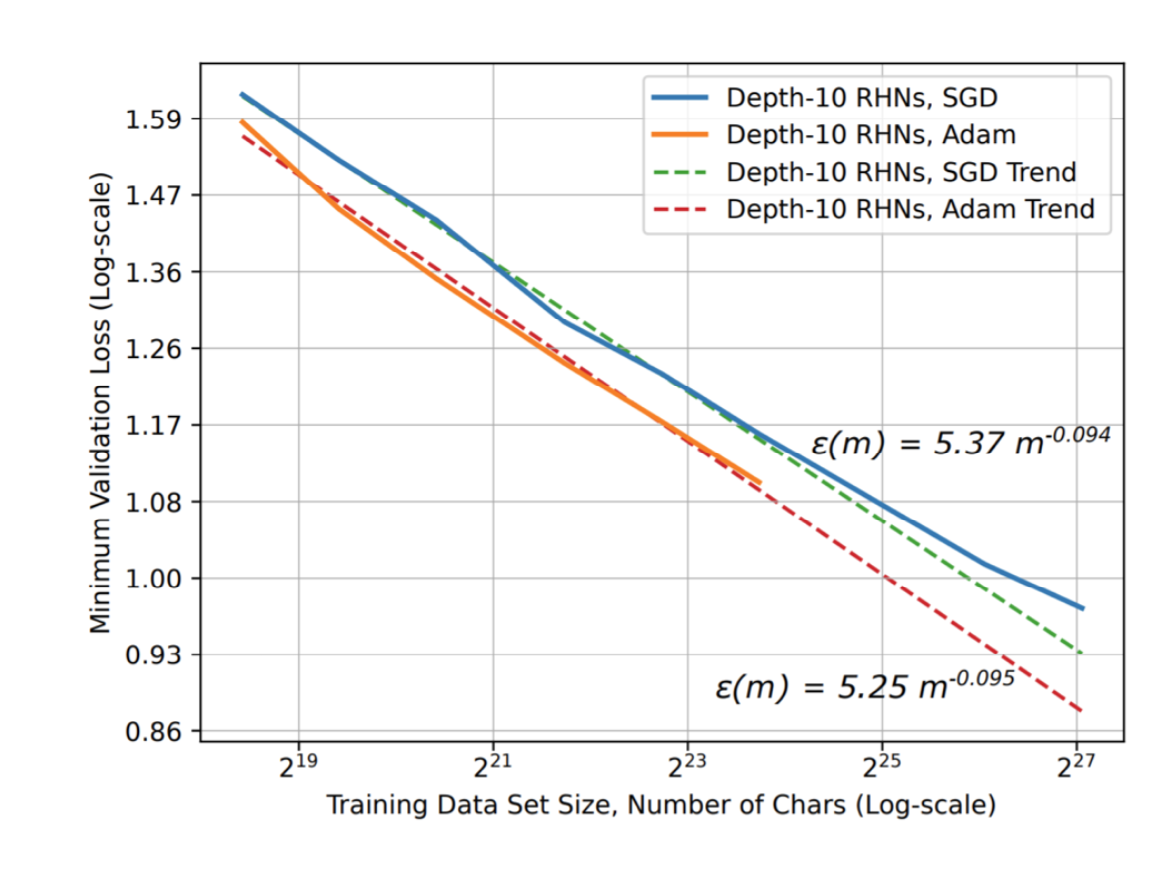
Adam vs SGD

Hestness 2017 的实验里，Adam 往往在更广的数据范围内处于更低 loss 区间（趋势线也更优）。

8.3 深度 vs 宽度：深度需要“过阈值”，之后参数总量更关键

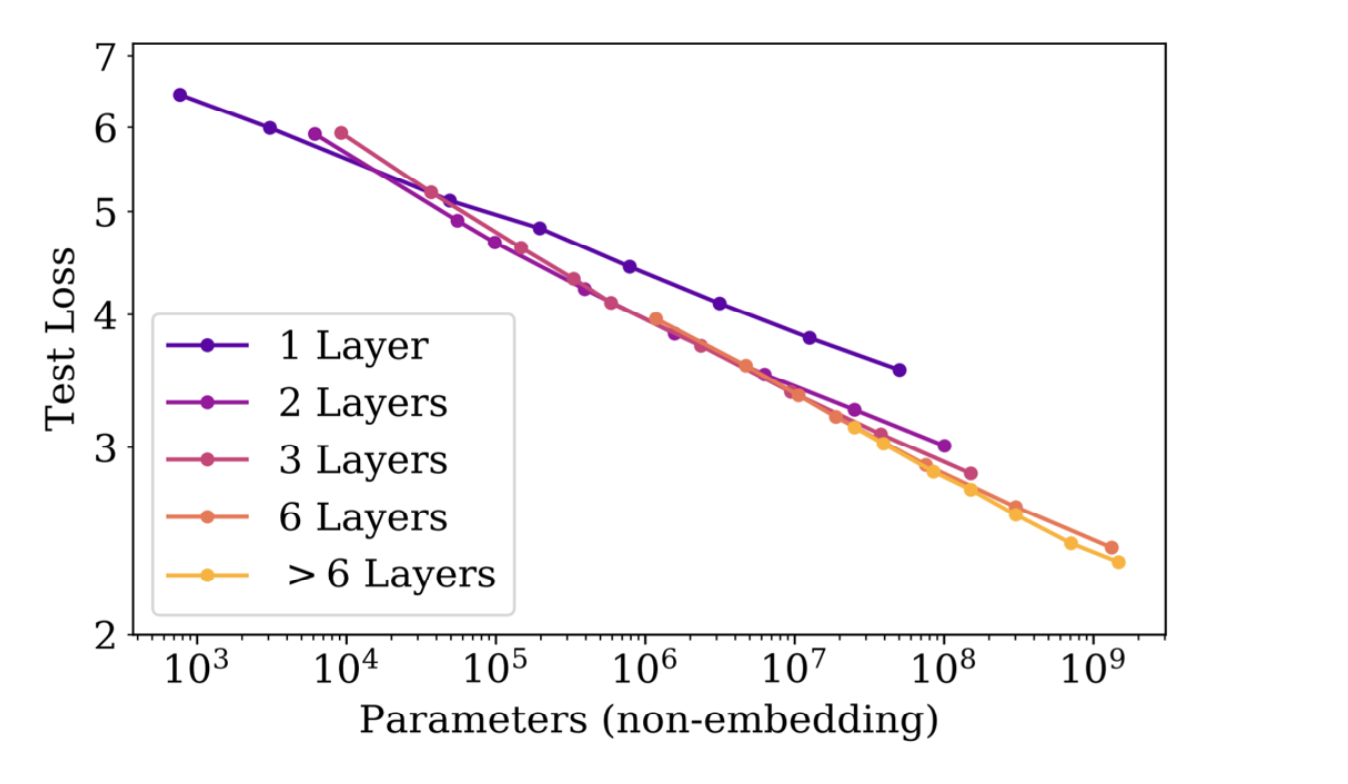
Depth vs width：阈值与递减收益

课堂要点：

从 1 层到 2 层可能是“质变”（非线性变换次数过少不够用）。
超过一定阈值后（课堂图中提到约 $10^7$ 参数尺度附近），继续加深往往边际收益递减。

8.4 关键口径：别把 embedding 参数当成“有效参数”

当用“总参数量（含 embedding）”画 scaling 时，会出现较大散乱；改用“非 embedding 参数量”后，曲线会更干净地重合：

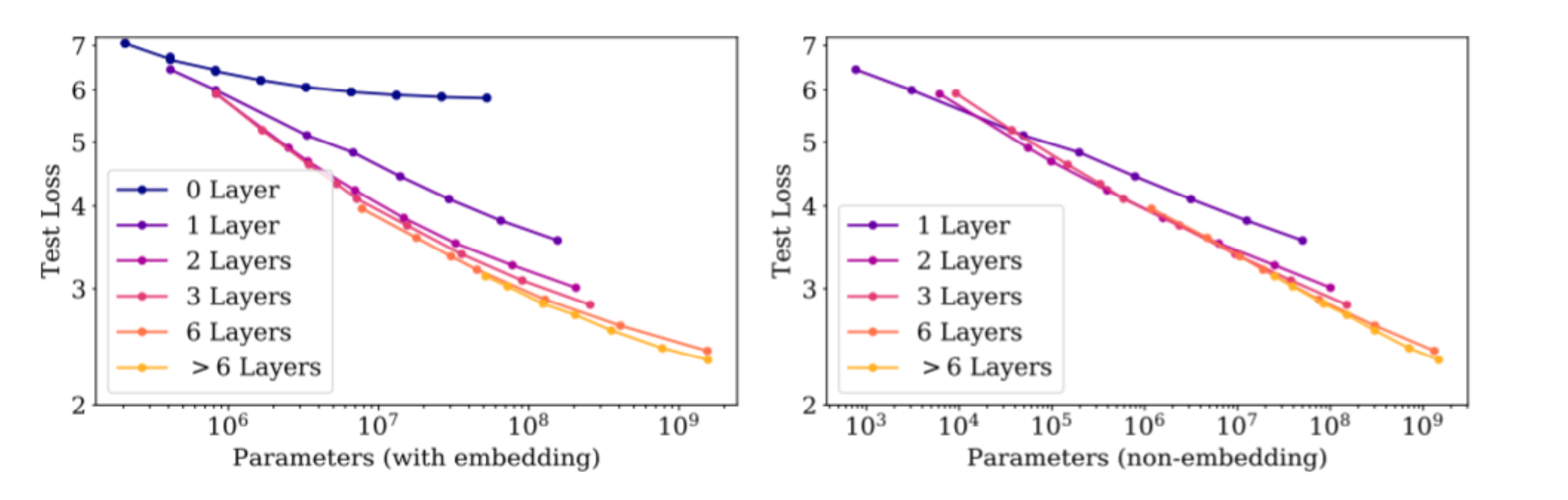
含 embedding vs 非 embedding 参数

直觉：

embedding 更像一个巨大的查表字典（lookup table），对“智能计算”贡献不如 Transformer block 的 attention/MLP。
因而 scaling law 更适用于 $N_{\text{non-embedding}}$（非嵌入参数）。

延伸：在 MoE（Mixture of Experts）里，“总参数量”也可能是虚的；更贴近缩放/计算成本的指标往往是每次前向激活的 active parameters（以及由此带来的实际 compute）。

8.5 形状超参：一个“平底碗”——Scale dominates shape

同样的参数量可以有不同形状（深而窄 / 浅而宽、FFN ratio、head dim）。Kaplan 2020 的结果是：曲面像一个底部很宽的碗，很多设置“差不多就行”。

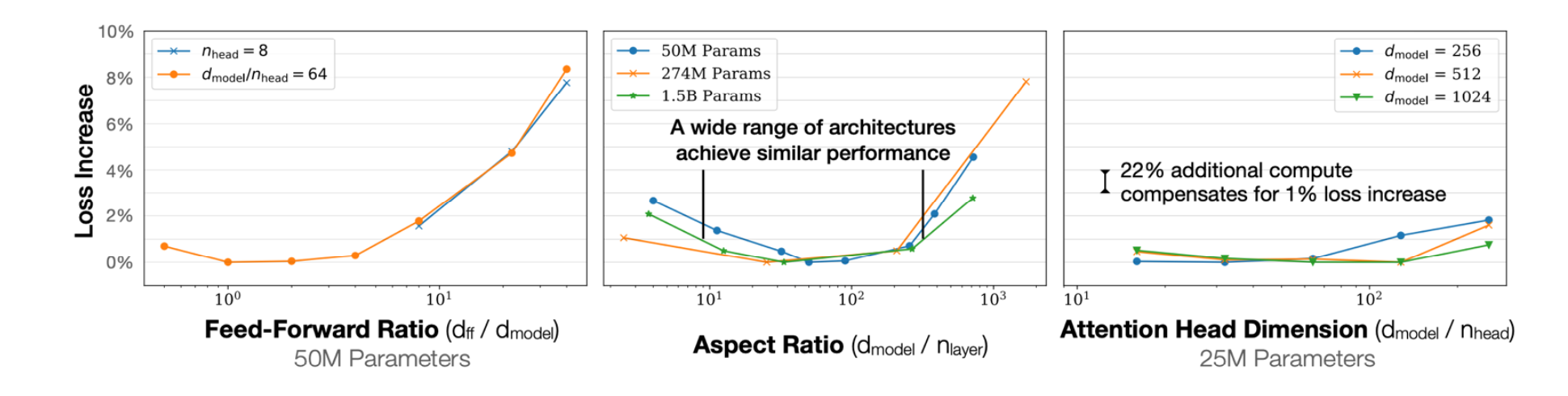
shape 超参：宽平的最优区

并且有一句很“工程”的注释： “22% additional compute compensates for 1% loss increase.”
（形状搞砸一点，多花点算力通常就能补回来。）

9. Batch size：存在临界点，训练后期需要更大 batch

9.1 为什么 batch 不是越大越好？

直觉图：小 batch 噪声大但每步便宜；大 batch 方向更准但每步昂贵。

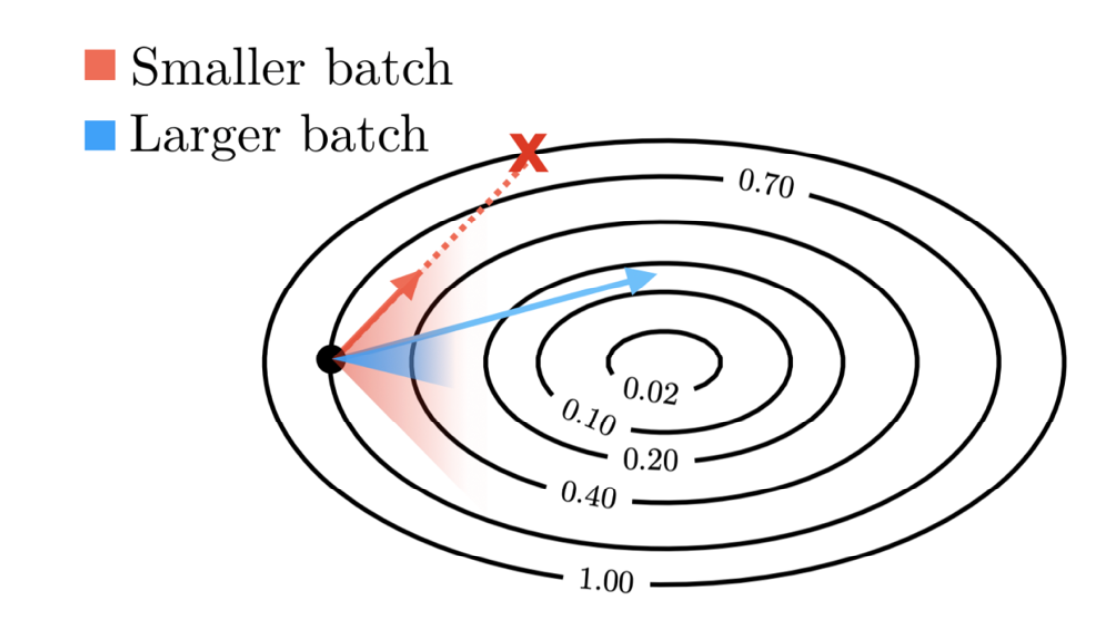
SGD 走路直觉

关键是“临界 batch size”：超过它，再加 batch 收益很小（并行效率开始失效）。

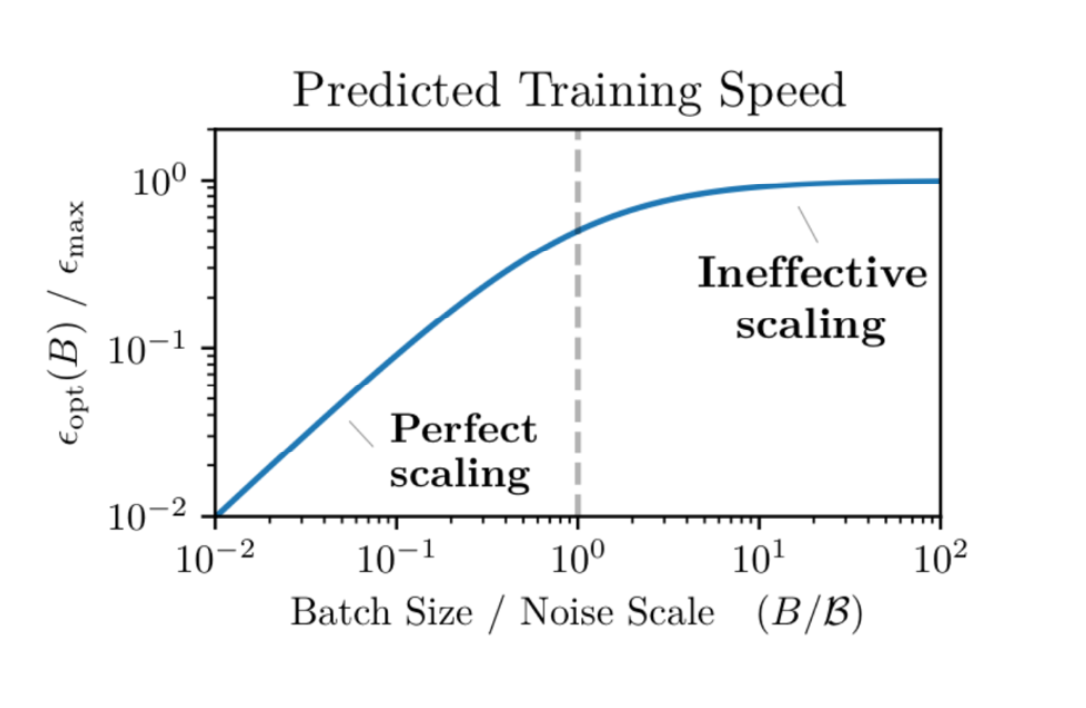
Critical batch size

概念性定义（课堂给出的写法）： $\text{Critical Batch} \approx \frac{\text{达到目标 loss 所需的最小样本数}}{\text{达到目标 loss 所需的最小步数}}$

9.2 Golden rule：目标 loss 越小，需要的 batch 越大

训练越到后期，loss 越小，噪声越难压，需要的 batch 会非常夸张地增大（图上指数约为 -4.8）：

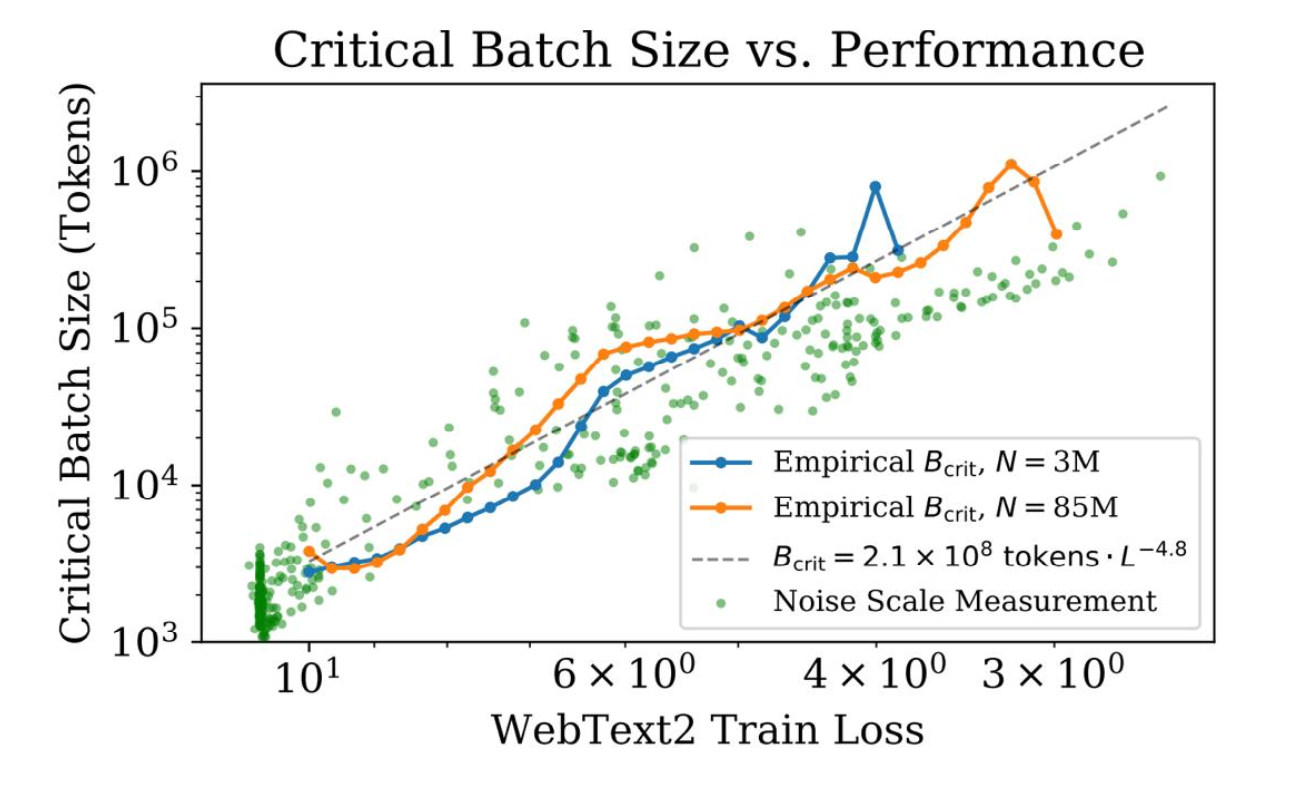
loss 下降时 critical batch 爆炸增长

工程落地：

不要全程固定 batch。
做 batch size warmup / ramp-up：随训练进度逐步增大全局 batch。

10. 训练时间不会线性爆炸：步数近似恒定，靠更大 batch 吃掉更多算力

当模型与算力扩大很多倍时，如果保持 batch 不变，只能靠增加步数，训练会变得极长；但 scaling 的结论更支持另一条路：步数规模上近似恒定，主要通过更大的 batch 来消耗更多算力。

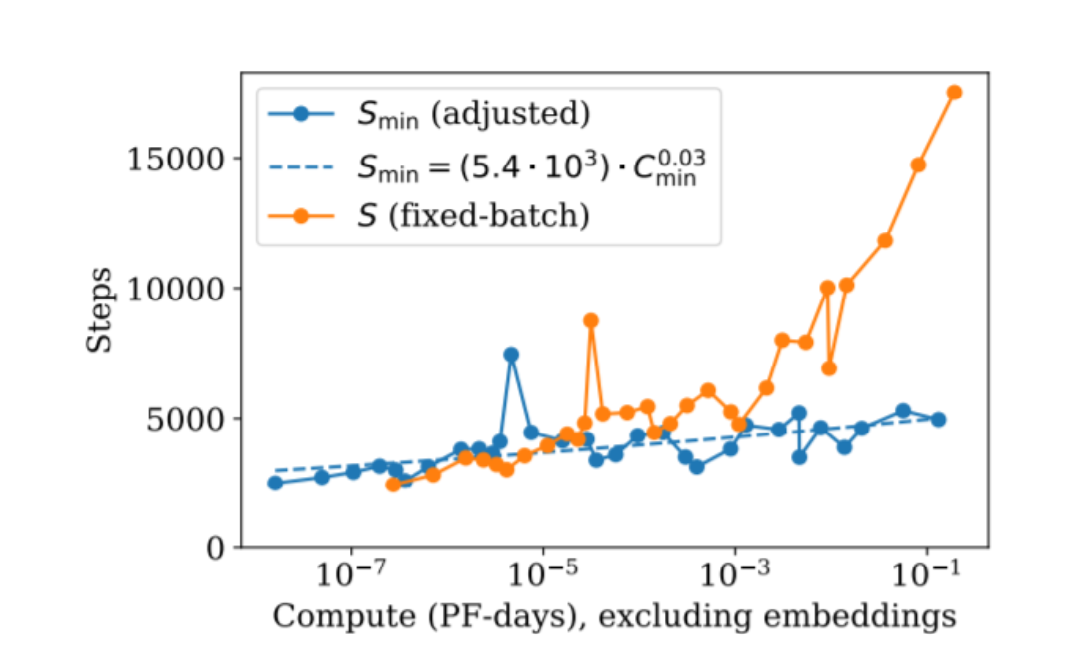
steps vs compute：调整 batch 后步数几乎不变

一个常见口径： $S_{\min} \propto C_{\min}^{0.03}$

指数很小，意味着算力上去很多倍，所需优化步数只会轻微变化。这也解释了为什么这对数据并行是“好消息”：增 batch 很容易通过堆卡实现。

11. 学习率：muP 让“小模型调参 → 大模型复用”更可行

11.1 痛点：标准做法下最佳学习率会随宽度漂移

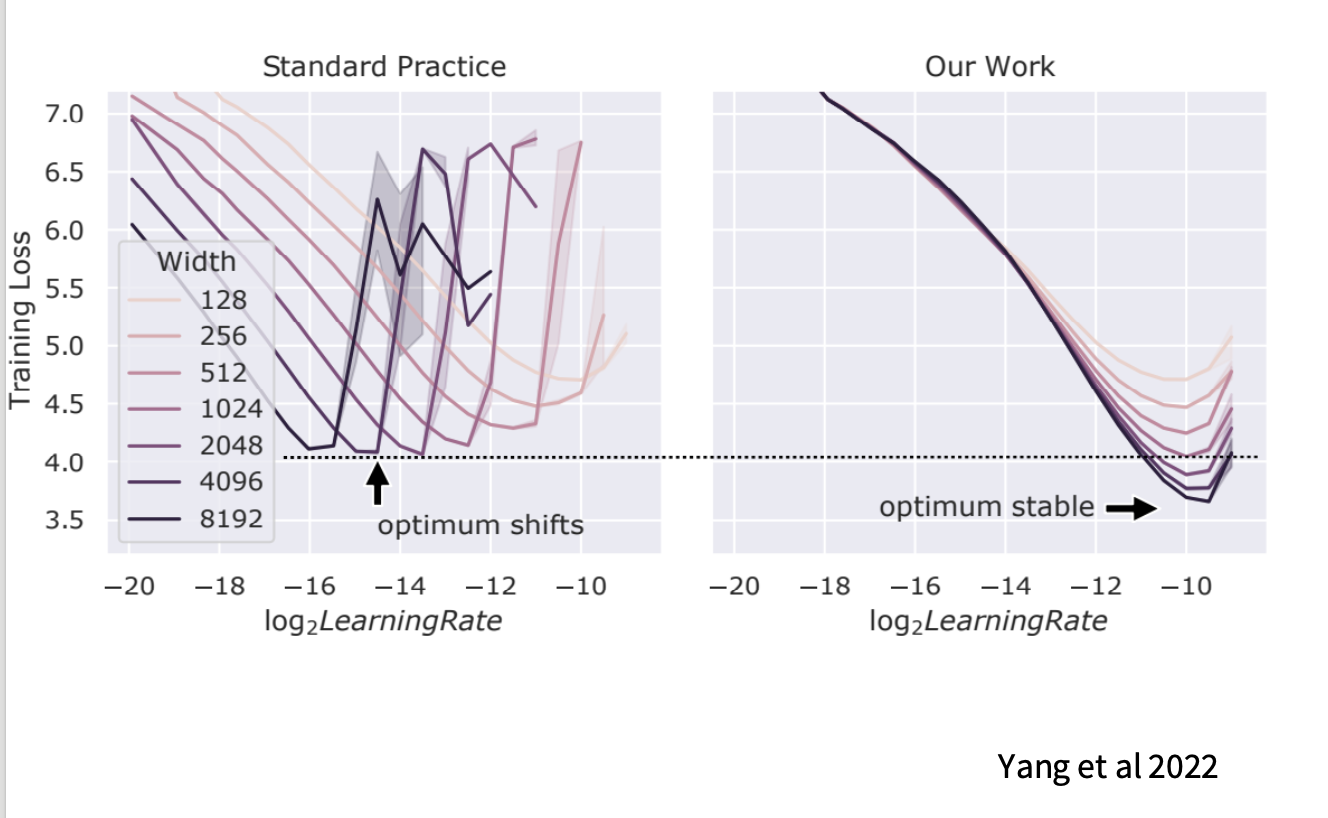
标准实践：最佳 LR 漂移

11.2 muP：把漂移“钉住”，实现零样本超参迁移

muP（Maximal Update Parametrization，Greg Yang 等）通过对初始化/学习率的宽度依赖做系统修正，使不同宽度模型的曲线更可比，最佳 LR 位置更稳定：

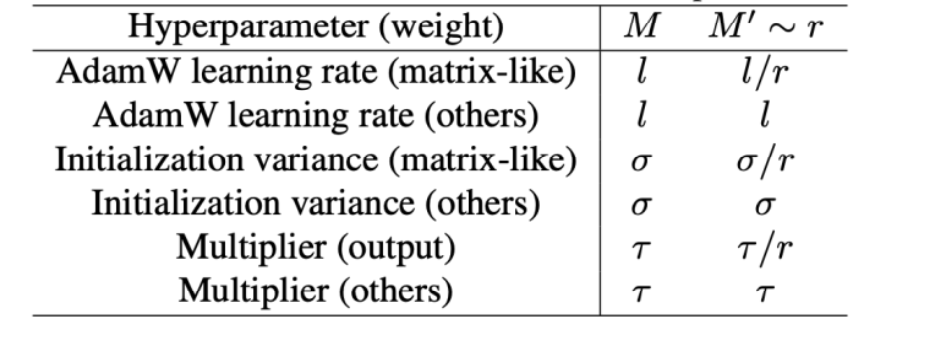
muP：曲线重合与最佳 LR 稳定

工程意义：能更放心地在小模型上找一套较优超参，再迁移到大模型，降低昂贵搜索成本。

12. 联合缩放：数据量与模型大小必须一起变（valley / Pareto）

只加数据不加模型会撞上“模型瓶颈”，只加模型不加数据会撞上“数据瓶颈”。因此需要联合公式来刻画 trade-off。

12.1 现象：小模型吃不下海量数据（数据被浪费）

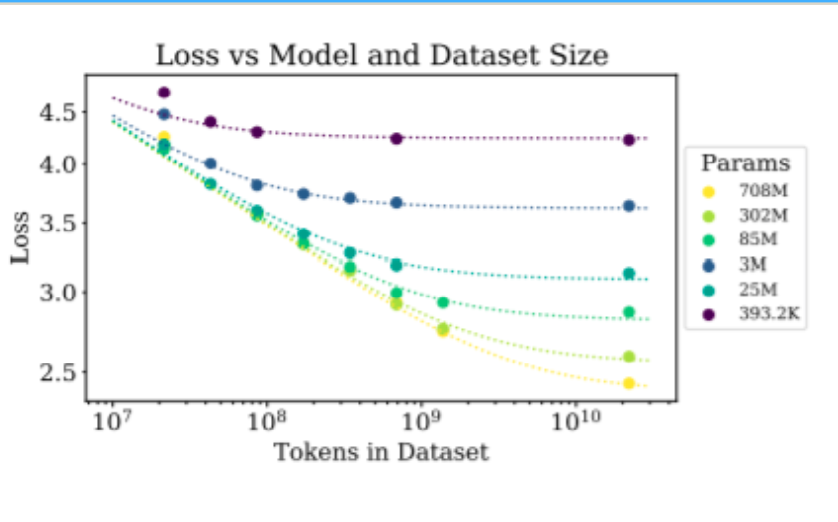
小模型很快饱和

12.2 两类联合形式（课堂提到的两个代表）

为避免符号混乱：这一小节沿用论文/幻灯片常见写法，用 $n$ 表示数据量（对应前文 $D$），用 $m$ 表示模型大小（对应前文 $N$）。

Rosenfeld+ 2020（加法直觉）： $\text{Error} = n^{-\alpha} + m^{-\beta} + C$

Kaplan+ 2020（另一种耦合写法，课堂简化口径）： $\text{Error} = \left[m^{-\alpha} + n^{-1}\right]^{\beta}$

两者的共同点：必须同时增大 $n$（数据）与 $m$（模型）才能持续下降。

12.3 3D 视角：误差曲面像山谷，最优路径沿“对角线”

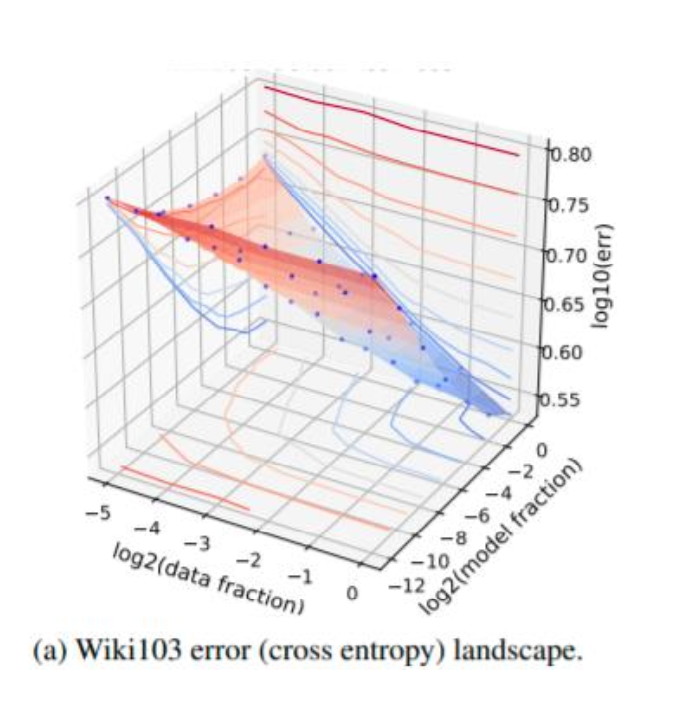
3D loss landscape：沿 valley 走

13. 外推真的可用：用小模型数据预测大模型，准得可怕

用很小的模型/数据去拟合 $\alpha,\beta,C$，再外推到大规模点，预测值与真实值往往高度一致：

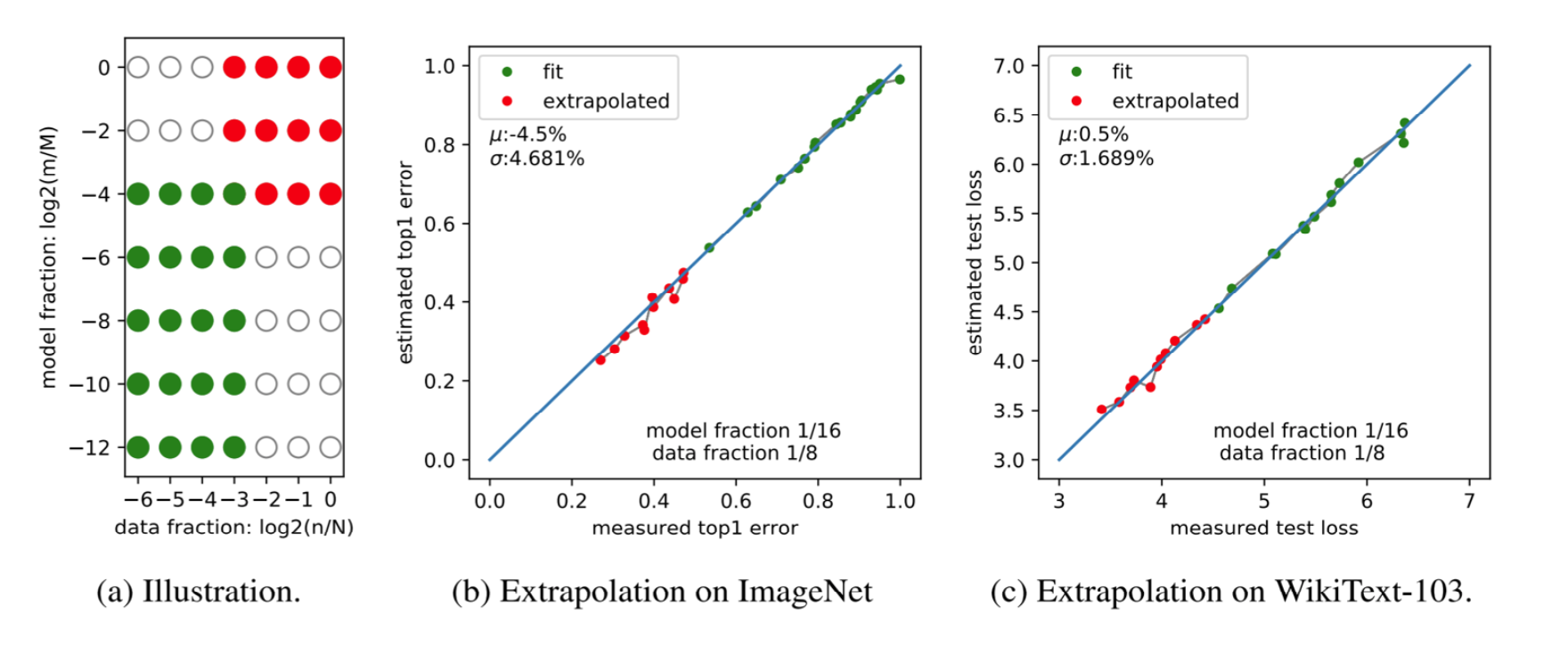
extrapolation 验证

这也是 scaling laws 能从“经验”变成“工程方法”的关键：它不仅解释过去，还能指导未来预算决策。

14. 固定算力预算：Kaplan 的“香蕉曲线”与结论（后来被反转）

当算力预算固定时，一个常用近似是： $C \approx 6 \times N \times D$

于是 $C$ 固定意味着 $N$ 与 $D$ 是此消彼长的零和分配：做大模型就得少喂数据，喂更多数据就得模型更小。

14.1 香蕉曲线与包络线（Pareto frontier）

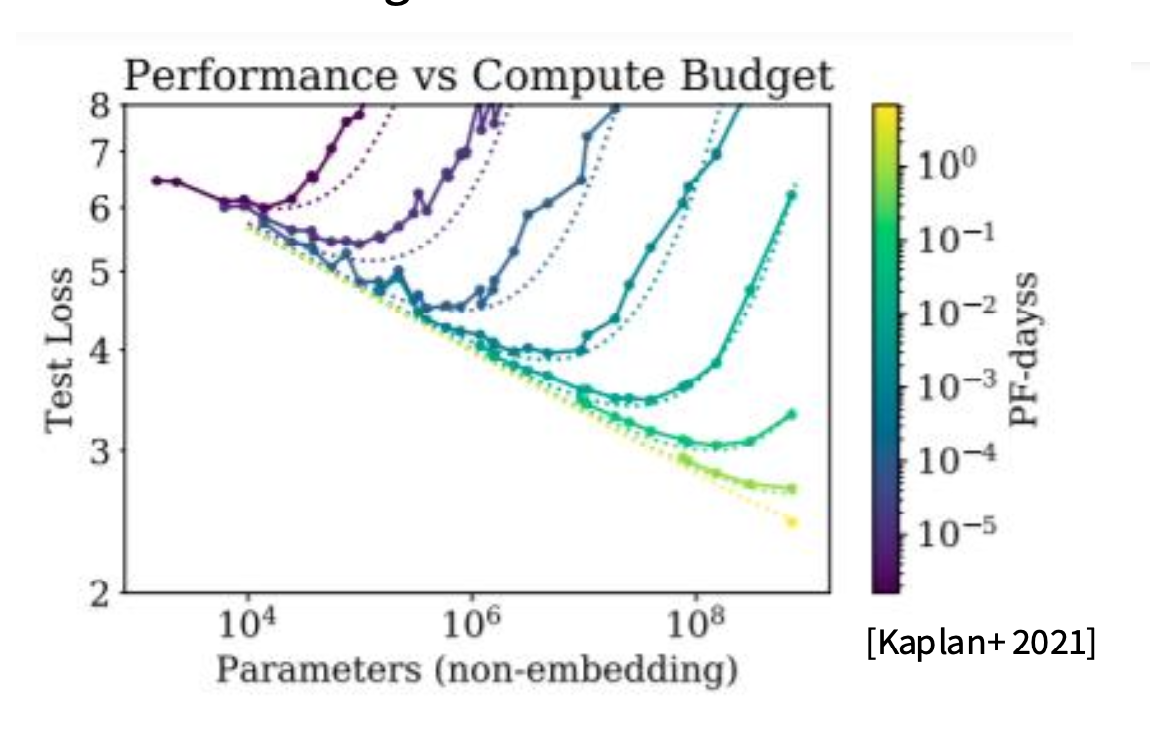
fixed compute 下的包络线

Kaplan 2020 当时的结论倾向于： 大模型（哪怕欠训练）通常优于小模型（哪怕训练得很充分）
这直接推动了当时“模型越大越好”的趋势（如 GPT-3 175B）。

15. Chinchilla 反转：更小模型 + 更多数据（参数与数据更接近 1:1）

Hoffman et al. 2022（Chinchilla）指出 Kaplan 的最优配比偏向“模型过大、数据过少”。在固定算力下，compute-optimal 的策略更接近：

模型参数与训练数据 按更接近同比例的方式增长（常被口语化为 N:D ≈ 1:1 的“配比思维”）。
许多当时的大模型落在“过大”的区域，造成算力浪费。

课堂里常用几个“定位点”来帮助理解这种浪费：

Megatron-Turing NLG 530B：参数巨大但数据相对不足，按 Chinchilla 视角属于明显 oversize。
GPT-3 175B：也更偏向“模型大、读书少”的一侧。
Chinchilla 70B：在相近总算力下，用更小模型训练更多 tokens（课堂提到可达到 Gopher 280B 的约 4 倍数据量），结果在多项指标上反超更大的模型。

16. 为什么 Kaplan 与 Chinchilla 会差这么多？根因是学习率调度与训练步数匹配

一个看似微小但足以改变结论的细节：cosine learning rate schedule 的周期长度必须与实际训练步数匹配。
如果用同一条 schedule 去覆盖不同训练长度，并在中途截断，就会导致某些点“没收敛到该收敛的位置”，从而扭曲拟合出来的 scaling 曲线。

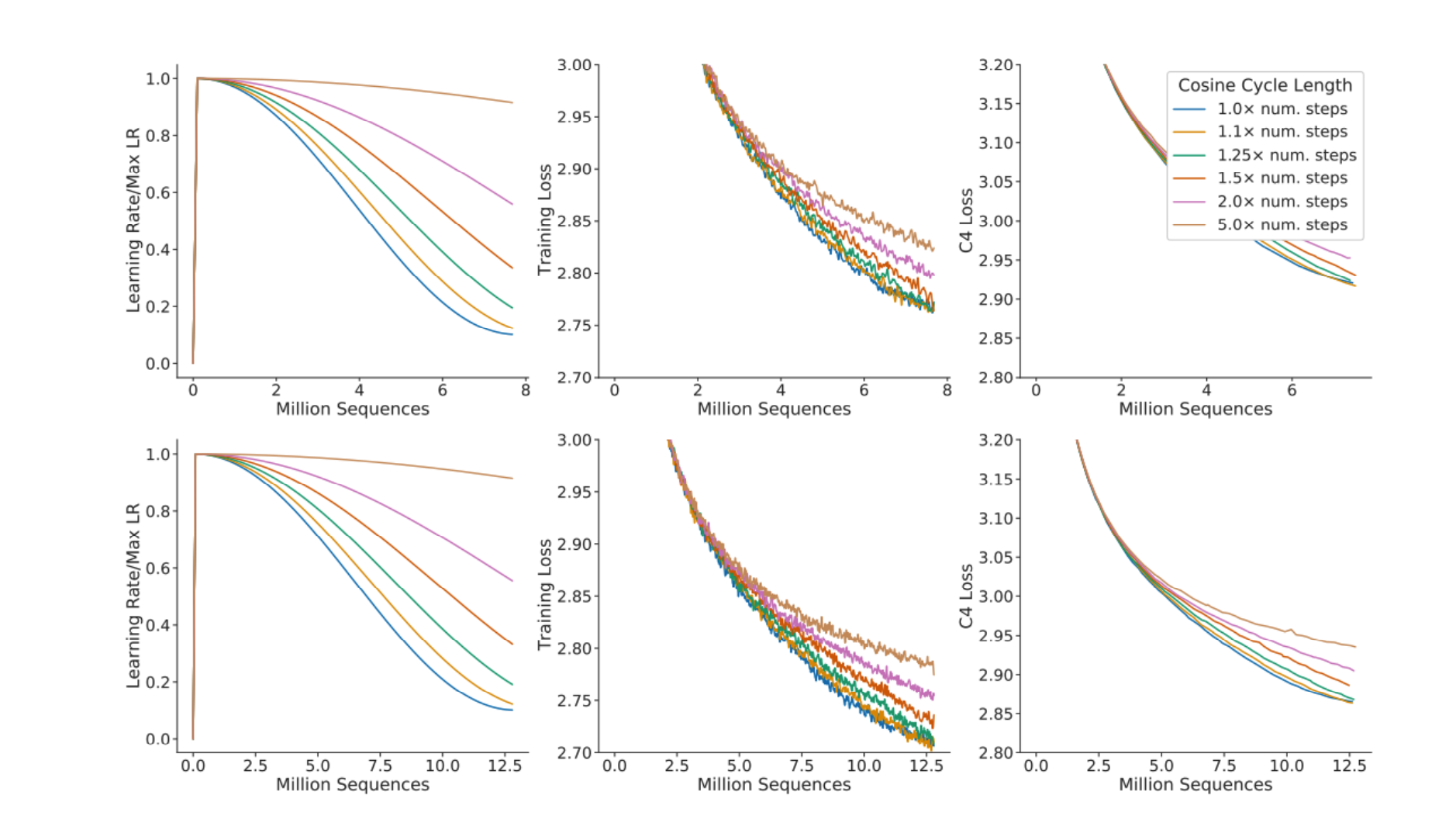
LR schedule mismatch 导致拟合偏差

课堂总结口径：

Kaplan 的偏差不是数学形式错了，而是实验设置里对 LR schedule 与训练时长的匹配不够严格。
Chinchilla 修正后，得到了更“数据友好”的 compute-optimal 配比，从而推动了后续更重视“多读书（tokens）”的训练策略（也影响了 LLaMA 系列等）。

17. 一页实践清单：用 scaling laws 指导训练决策

先确认你在哪个瓶颈上： compute-limited / data-limited / model-limited（不要只盯单变量）。
把数据当成两件事： quantity 决定能走多远，quality/composition 主要决定起跑线（offset）与泛化稳健性。
数据会用完： 一旦开始大量重复，要用“有效数据量”视角重新评估，并考虑“模型更大一点、训练更少 tokens”的转移。
形状超参别过度纠结： 在合理范围内，scale 往往更重要；把精力放在 N/D/compute 的配比与数据工程上。
batch 要随训练进度变： 目标 loss 越低，critical batch 越大；用 batch ramp-up 提升整体效率。
LR/超参迁移要有方法： muP 的思想是让“小模型找超参”更可复用；同时避免 schedule 与训练步数不匹配导致的错误结论。

上篇Paralism Basic

下篇LLM 推理（Inference）笔记梳理：为什么慢、慢在哪里、怎么加速

1. Scaling law 是什么：为什么 log-log 上是一条直线？