LLM 推理（Inference）性能推导

1. 先把推理过程拆开：Prefill vs Decode

同一个模型，在推理时其实有两个阶段：

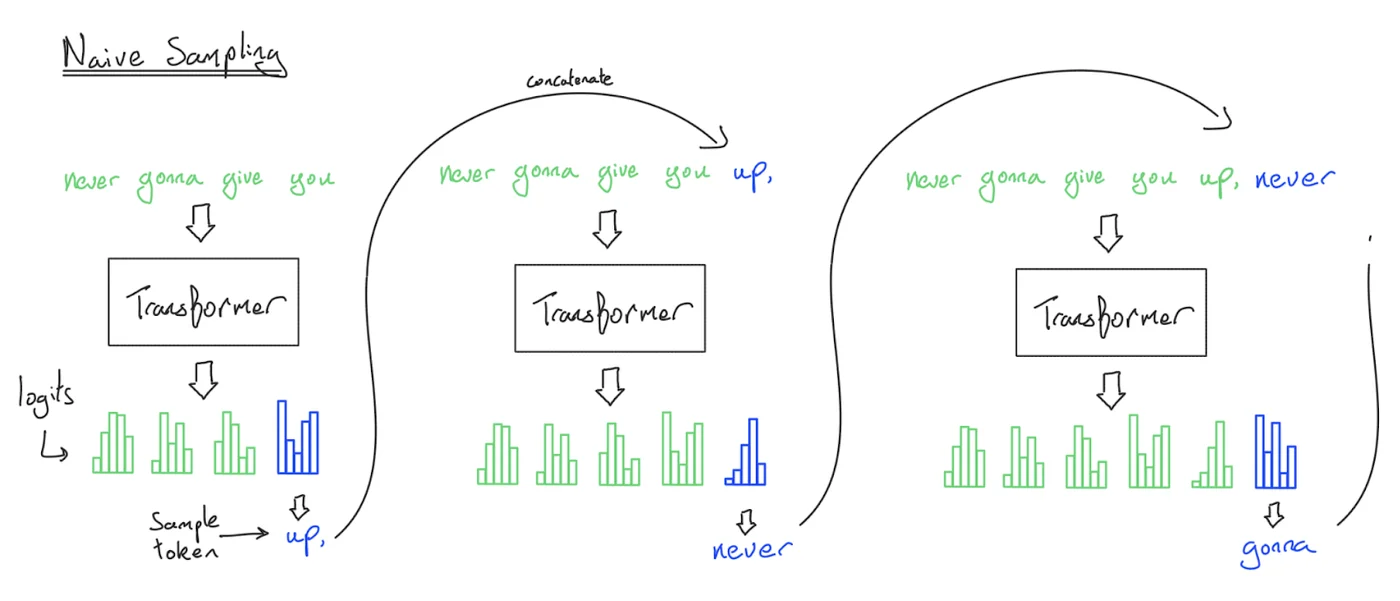
1. Prefill（预填充）：把 prompt 一次性喂进去，算出每层的隐藏状态，同时把 K/V 写入 KV Cache。这个阶段对 prompt 的 token 可并行，形态更像训练，通常更接近 compute-bound。
2. Decode（生成/解码）：自回归逐 token 生成。每一步只处理 “当前 1 个 token”，需要读取（并更新）已有的 KV Cache。这个阶段通常 memory-bound，决定了 tokens/s。

2. 符号约定

2.1 变量的定义

为了方便推导，定义变量：

• B：batch size（并发请求数）
• S：上下文长度（prompt + 已生成），在 decode 时随时间增长
• T：当前这次计算处理的 token 数；prefill 时可取一段（常见 T≈S），decode 时 T=1
• D：模型隐藏维度
• L：层数
• N：Query 头数
• K：Key/Value 头数（GQA/MQA 下可能 K < N）
• G：每个 KV 头共享的 Q 头数（GQA 分组大小），G = N / K
• H：单头维度，通常 D = N·H
• F：MLP 中间维度（常用近似 F = 4D）
• V：词表大小

Transformer 示意图：

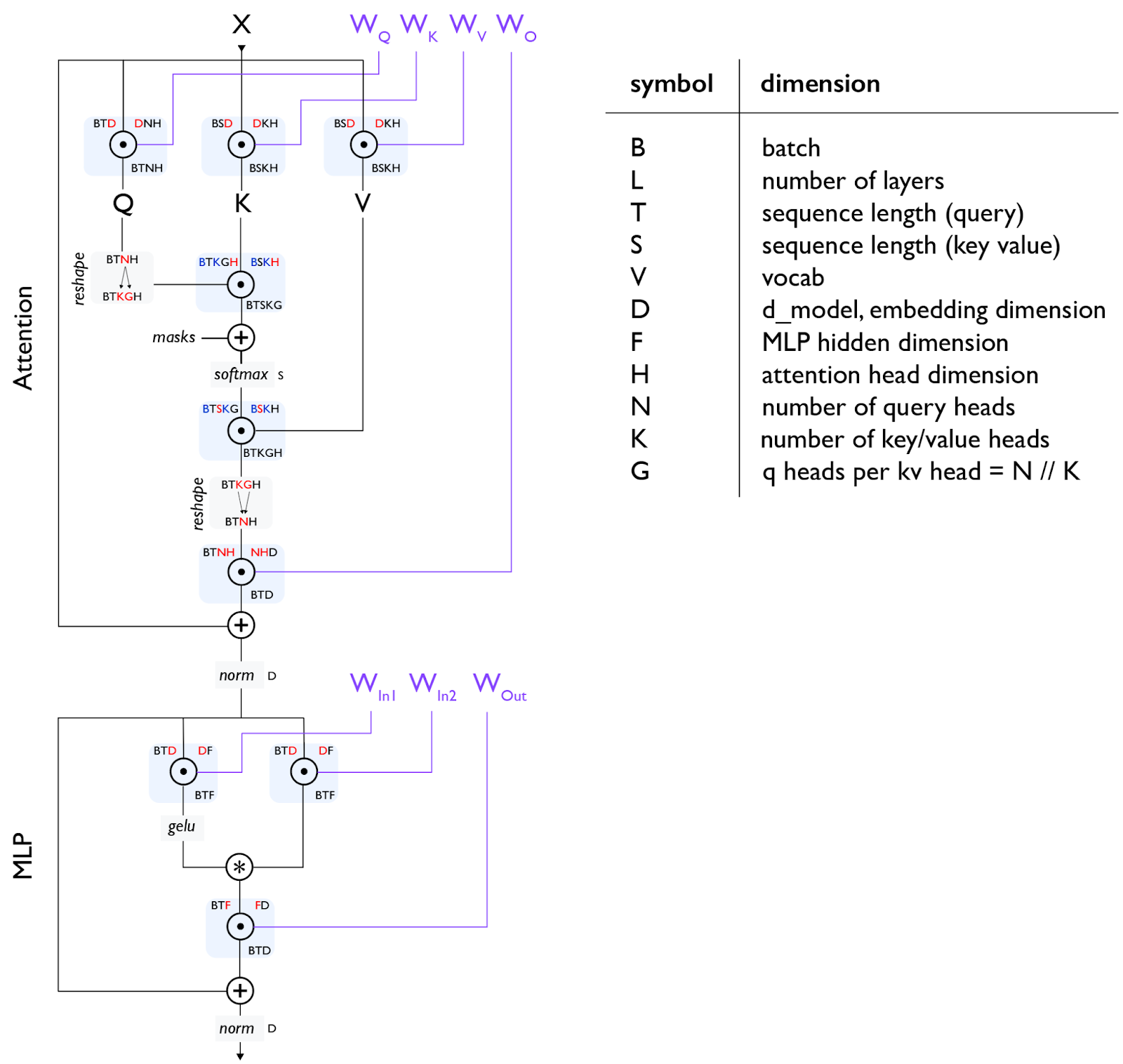
2.2 Attention 模块

这一部分是推理时 计算密集（Prefill） 与 内存密集（Decode） 的核心。

(1) 线性投影 (Projection)

输入 $X (B, T, D)$ 分别与 $W_Q, W_K, W_V$ 相乘（这里的 $T$ 表示“本次一起算的 token 数”，prefill 时通常较大，decode 时为 1）：

• $Q$：维度从 $(B, T, D)$ 变为 $(B, T, N, H)$（通过 $W_Q: D \to N!H$）。
• $K, V$：维度从 $(B, T, D)$ 变为 $(B, T, K, H)$（通过 $W_K, W_V: D \to K!H$）。
• 性能要点：推理时会把本次算出来的 $K/V$ 追加写入 KV Cache，使得缓存形状随上下文增长为 $(B, S, K, H)$。由于 $K < N$，KV Cache 显存占用比传统 MHA（$K=N$）显著降低。

(2) 形状变换 (Reshape for GQA)

注意图中中间的 reshape 步骤：

• $Q$ 被拆解为 $(B, T, K, G, H)$，即 $K$ 个组，每组 $G$ 个头。
• 这是为了让每组内的 $G$ 个 $Q$ 头共享同一个 $K$ 和 $V$ 头进行计算。

(3) 注意力计算 (Scaled Dot-Product Attention)

• Score: $Q \cdot K^T \to (B, T, K, G, S)$。
• Mask & Softmax: 在 $S$ 维度上做归一化。
• Context Vector: Score 与 $V$ 相乘，得到 $(B, T, K, G, H)$，最后合并回 $(B, T, N, H)$。

(4) 输出投影 (Output Projection)

• 通过 $W_O$ 将维度从 $(B, T, NH)$ 映射回 $(B, T, D)$，并加上残差连接（Residual Connection）。

2.3 MLP 模块：计算的大头

图中展示的是一种 Gated MLP 结构（常见于 SwiGLU 激活函数）：

• 并行支路：输入经过两个投影层 $W_{In1}$ 和 $W_{In2}$。
  • 维度从 $D$ 映射到 $F$。
• 激活与门控：其中一条支路经过激活函数（图中注为 gelu，Llama 等模型常用 silu），然后与另一条支路进行 元素级乘法 (Element-wise Product, $\ast$)。
• 下投影 (Down Projection)：通过 $W_{Out}$ 将维度从 $F$ 映射回 $D$。
• 性能要点：MLP 的计算量（FLOPs）通常占整个 Transformer Block 的 2/3 左右，但它的权重访问是静态的，不涉及 KV Cache 的动态增长。

3. “推理性能主线”：共享权重 vs 私有 KV

推理瓶颈的根源可以用一句话概括：

Decode 阶段每步都要“读很多、算很少”。

而“读很多”主要来自两类数据：

• 共享权重（Shared Weights）：MLP/Attention 的权重矩阵，对所有请求/所有 token 都是同一份
• 私有状态（Private States）：每条序列自己的 KV Cache，大小随 S、B、L 线性长。

两类层在 decode 时的性质很不一样：

• MLP 层：主要是矩阵乘（读权重 + 少量激活），权重共享 → batch 越大越划算。
• Attention 层：除了读权重，还要读“每条序列私有”的 KV Cache → batch 变大时 KV 读也同比变大，算术强度几乎不涨。

4. 为什么 decode 慢：算术强度（Arithmetic Intensity）+ Roofline

4.1 算术强度（Arithmetic Intensity）

核心概念： \(AI=\frac{\text{FLOPs}}{\text{Bytes moved}}\)

硬件视角（Roofline）：当 AI 低到一定程度时，性能上限由 内存带宽决定，而不是由算力（TFLOPS）决定。

以 A100 为例（数量级直觉）：

• FP16 算力 ~312 TFLOPS
• HBM 带宽 ~2 TB/s
• “跑满算力”需要的 AI 约 312/2≈156（ops/byte 量级）

decode 时单请求（B=1）的 AI 往往接近 1，因此会出现“算力空转、等数据”的现象。

4.2 MLP 算术强度分析

4.2.1 从一个 GEMM 看出 batch 的意义

考虑矩阵乘 Y = XW，其中 X∈R^{B×D}，W∈R^{D×F}：

• FLOPs：2·B·D·F
• Bytes（FP16，2 bytes）：约 2·B·D + 2·D·F + 2·B·F

在推理常见的近似下（F≈4D 且 B ≪ D），2·D·F（读权重）是主项，于是： \(AI \approx B\)

这解释了：MLP 想要更高利用率，本质上需要更大的 batch 来“摊薄读权重”。

4.2.2 MLP的Prefill 高 AI，Decode 低 AI

以 Llama 常见的 SwiGLU MLP 为例（Up/Gate/Down 三个矩阵），如果忽略算子融合带来的缓存复用，粗略估计得到：

• FLOPs：≈ 6·B·T·D·F
• Bytes：包含读写激活 + 读权重，其中推理常见近似是 读权重占主导

当 B·T ≪ D,F（模型大、当前批量小）时： \(AI_{\text{MLP}} \approx B\cdot T\)

于是：

• Prefill：T≈S，AI≈B·S → 往往 compute-bound（“像训练一样快”）
• Decode：T=1，AI≈B → 往往 memory-bound（除非 batch 大到离谱）

4.3 Attention 算术强度分析

这一节想回答一个工程上很常见的直觉：MLP 可以靠增大 batch 摊薄读权重，但 attention 在 decode 阶段几乎“吃不进 batch”。

在 FlashAttention（避免把注意力矩阵写回 HBM）的理想化分析下：

• FLOPs：≈ 4·B·S·T·D
• Bytes：≈ 4·B·S·D + 4·B·T·D（读 K/V + 读/写 Q/Y）

得到算术强度： \(AI_{\text{Attn}}=\frac{S\cdot T}{S+T}\)

关键点：公式里没有 B，也没有 D。

两种典型场景：

• Prefill：T=S → AI≈S/2（prompt 越长越“算得动”）
• Decode：T=1 → AI≈S/(S+1)≈1（无论上下文多长都接近 1）

这就是常说的：decode 的 attention 是“天生 memory-bound”，batch 只能涨吞吐，很难涨单步利用率。

5. 推理显存、延迟、吞吐量

把推理资源拆成两块：参数 + KV Cache。

5.1 参数量（静态）

下面是一套“够用的估算”（对应 Llama/SwiGLU/GQA 的常见记法）：

num_params = 2*V*D + D*F*3*L + (2*D*N*H + 2*D*K*H)*L

• 2*V*D：embedding + unembedding
• D*F*3*L：SwiGLU MLP（Gate/Up/Down）
• (2*D*N*H + 2*D*K*H)*L：Attention（Wq/Wo + Wk/Wv），其中 K < N 体现 GQA/MQA 的节省

5.2 显存占用（动态 + 静态）

以 BF16/FP16（2 bytes）为例：

parameter_bytes = num_params * 2
# KV Cache 形状直觉：(L 层) × (S 个 token) × (K 个 KV 头) × (H head_dim) × (K/V 两份)
kv_cache_bytes_per_seq = L * S * (K*H) * 2 * 2  # (key+value) * (bf16 bytes)
total_memory = parameter_bytes + B * kv_cache_bytes_per_seq

直觉：

• parameter_bytes 固定不变
• KV Cache 是“每条序列私有”的动态状态：decode 每生成 1 个 token，就会在每层追加一行 K/V，所以它随 B 和 S 线性增长（以及随层数 L 线性增长），常常是 OOM 的主要来源
• 实际系统还会有额外开销（paged block、对齐、临时 workspace、激活等），但数量级上通常仍由 parameter_bytes 与 B * kv_cache_bytes_per_seq 主导

5.3 延迟与吞吐（memory-bound 近似）

在 decode 阶段，很多系统的第一近似是：

latency_per_token = bytes_moved / memory_bandwidth
throughput_tokens_per_sec = B / latency_per_token

这里的 bytes_moved 建议理解为 “生成 1 个 token 这一轮 forward 在 HBM 上的总读写流量”，而 decode 之所以容易 memory-bound，关键在于每层 attention 都需要读一遍历史 KV：

• KV 读（主项）：约 B * L * S * (K*H) * 2 * dtype_bytes（读 key+value）
• KV 写（次项）：约 B * L * (K*H) * 2 * dtype_bytes（把新 token 的 K/V 追加写入）
• 权重读：MLP/Projection 权重是共享的，batch 变大可摊薄；但 attention 的 KV 是私有的，batch 变大 KV 读也同比变大，因此单步算术强度很难上去

因此会出现经典 trade-off：

• 小 B：单用户延迟低，但吞吐差、成本高
• 大 B：吞吐高，但 KV Cache 更大、排队/调度带来的延迟更高，也更容易 OOM

常见工程策略：

• 复制模型副本：吞吐近似 ×M，单 token 延迟不变（但显存也 ×M）
• 模型分片（Tensor Parallel / Sharding）：把权重拆到多卡，等价于提升总带宽 → 有机会降低单 token 延迟
• 分阶段目标：TTFT（首 token）更多受 prefill 影响；tokens/s 更多受 decode 影响，两者的最优 batch 往往不同

到这里，瓶颈已经很清楚了：prefill 更像算力问题，decode 更像带宽问题。

• 减少 decode 需要搬运的字节（核心是 KV Cache）
• 在不浪费的前提下把 batch 做大（调度/内存管理）
• 让 decode 的“步数”变少（投机解码）

6. KV Cache 瘦身

目标很明确：让 B·S·L·(K·H) 这坨东西更小，从而：

• 更不容易 OOM（能塞更大 batch）
• decode 时读写更少（更低 latency / 更高吞吐）

6.1 GQA / MQA：用“共享 KV 头”换显存

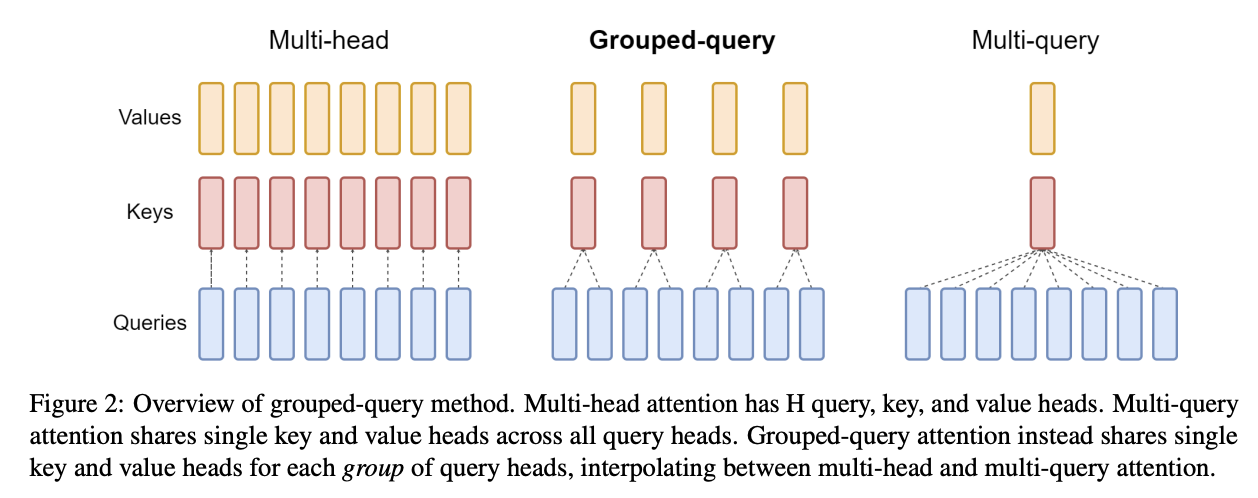
• MHA：N 个 Q 头对 N 个 KV 头（KV 最大）
• MQA：N 个 Q 头共享 1 个 KV 头（KV 最小，但精度风险更大）
• GQA：介于两者之间，N 个 Q，K 个 KV（1 < K < N），工业界主流折中（Llama 3 / Mistral 等）

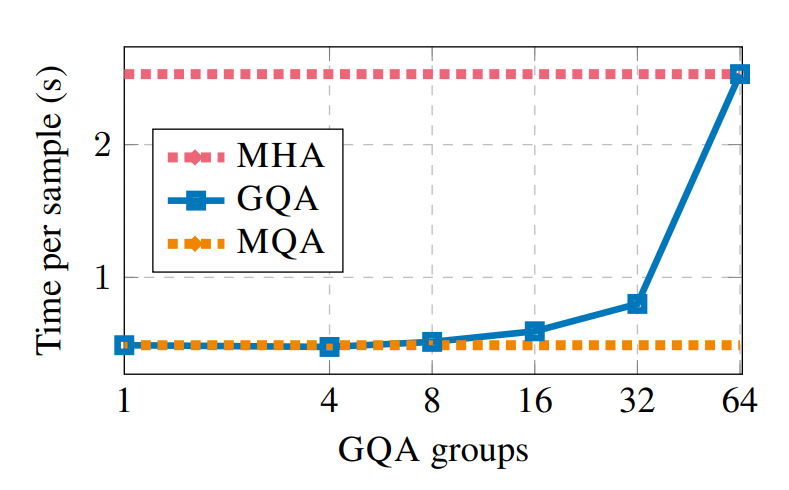
要点：GQA 本身不一定让单步 attention 变 compute-bound，但它能显著降低 KV Cache，使得 允许更大的 batch / 更少的 OOM，从而系统层面吞吐上去。

参考：https://arxiv.org/pdf/2305.13245

6.2 MLA（Multi-Head Latent Attention）：把 KV 投影到低秩 latent

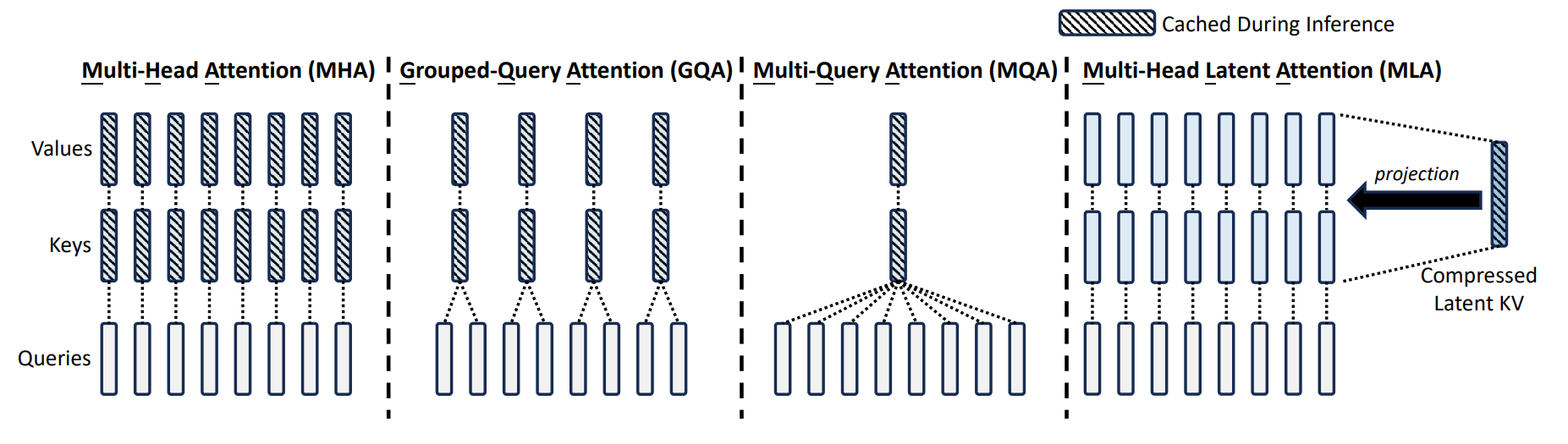
思路：不存完整 K/V，而是存一个低维 latent（比如从 N·H 压到 C），需要用时再“解码”回来（或等价地在 latent 空间完成计算）。

工程难点之一：RoPE 对位置敏感，通常需要保留一部分不压缩的维度承载位置信息（例如“压缩 512 + RoPE 64”）。

参考：https://arxiv.org/abs/2405.04434

6.3 CLA（Cross-Layer Attention）：跨层共享 KV

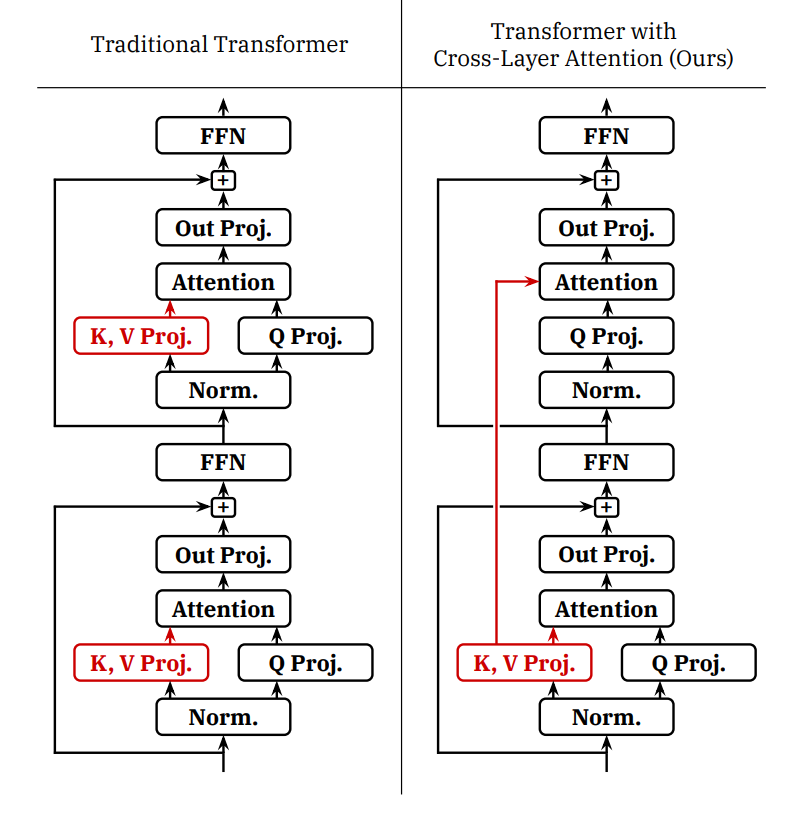
思路：GQA 是“同层头共享”，CLA 更激进：让不同层共享一份 KV（或某种共享结构），打破 KV Cache 随层数 L 线性增长的规律。

参考：https://arxiv.org/abs/2405.12981

6.4 Local / Sliding Window Attention：用“只看最近 W”换常数级 KV

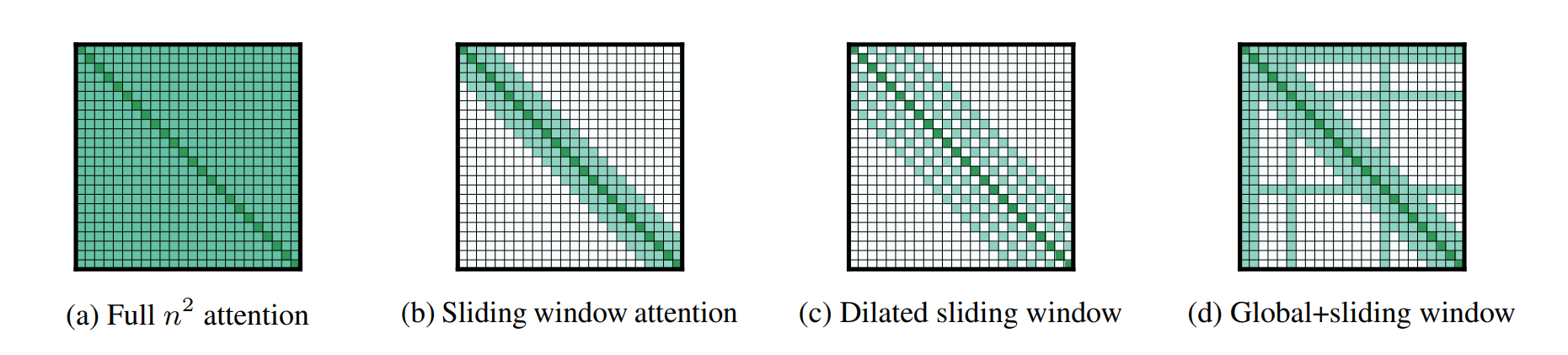
思路：每个 token 只 attend 最近 W 个 token，于是 KV Cache 不再随 S 增长，而是被窗口 W 截断：

• KV 规模从 O(S) 变为 O(W)（对超长上下文尤其重要）
• 代价是长距离依赖能力下降

常见混合策略：大多数层用 local，少数层用 global（例如“每 6 层里 5 层 local，1 层 global”），用少量全局层保住“智商”。

参考（Longformer）：https://arxiv.org/abs/2004.05150

7. Batch 做大但不浪费：Continuous Batching（Orca）

上一节解决的是“KV 太大”，这一节解决的是“batch 很难一直维持得足够大”。在真实线上流量里，请求长度不一、到达时间随机，静态 batching 往往要么等人（延迟高），要么 padding（浪费算力/显存），还会被“最慢请求”拖住。

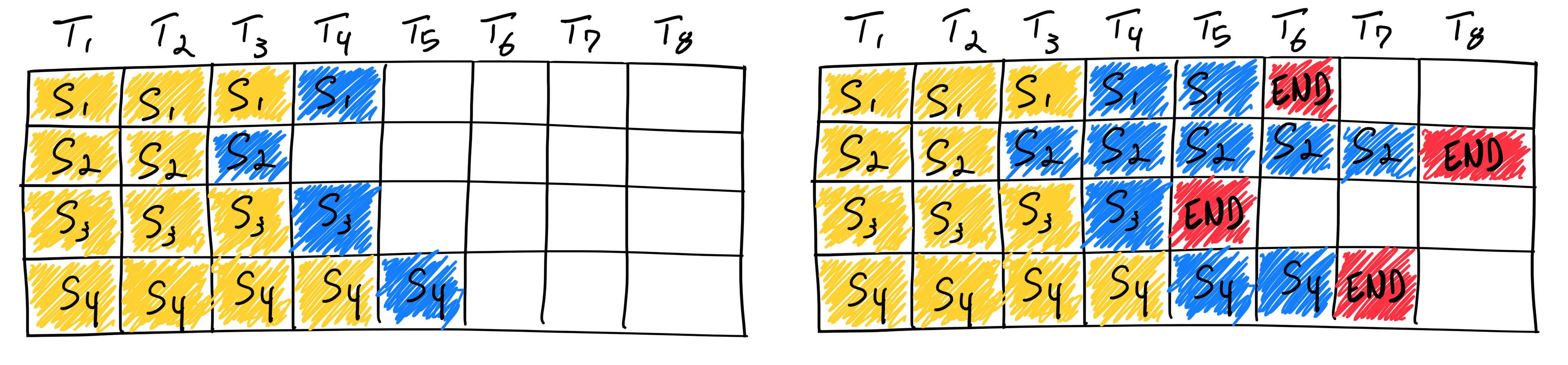
Orca 的两点核心思路：

1. Iteration-level scheduling：把调度粒度从“整个请求”变成“每生成 1 个 token”。每一步结束就：
   • 移除已完成请求
   • 插入新到请求
2. Selective batching：把不同算子按形态拆开处理
   • MLP/Linear：把所有请求当前 token 的隐藏向量直接拼成一个大矩阵（flatten），避免 padding
   • Attention：仍需按序列区分（或使用变长 attention kernel），避免把上下文搅在一起

8. KV Cache 管得更省：vLLM / PagedAttention

如果说 Orca 的重点是“让 batch 持续饱和”，那 vLLM 这类系统的重点是“让 KV Cache 的分配/复用更像操作系统的内存管理”，把碎片和浪费压到最低。

在 vLLM 之前，很多系统按 max_length 预分配一整段连续 KV Cache：用户早停会导致 内部碎片；显存不连续会导致 外部碎片。

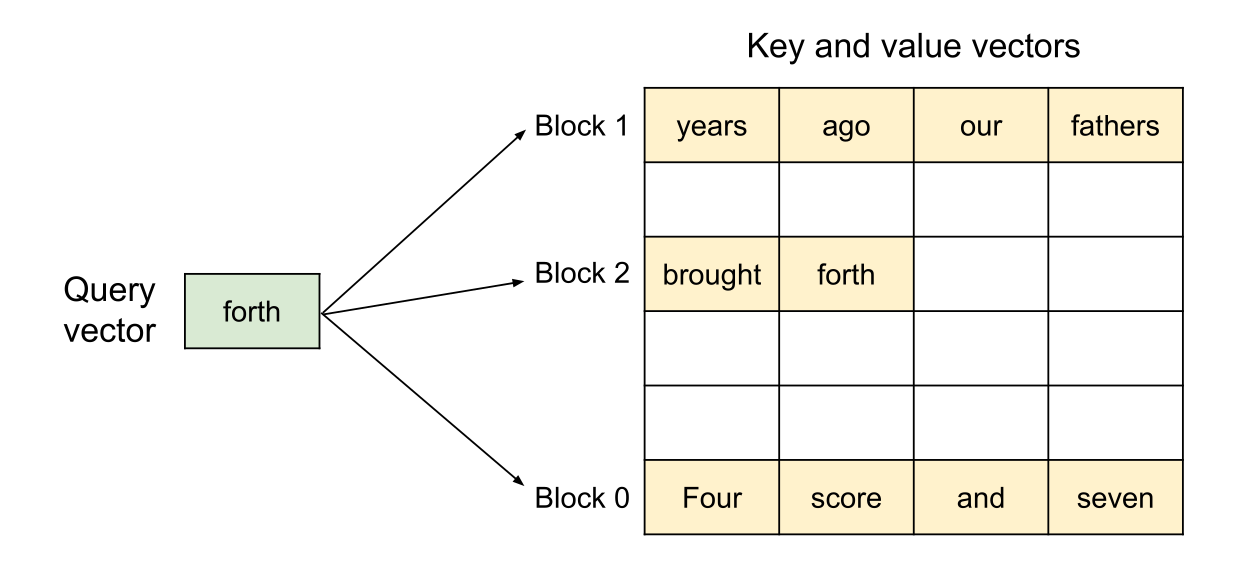
PagedAttention 的核心是把 KV Cache 切成固定大小 block（像 OS 分页）：

• 按需增长：生成到哪儿就分配到哪儿
• 物理不连续：用“页表/索引”把逻辑连续映射到物理离散

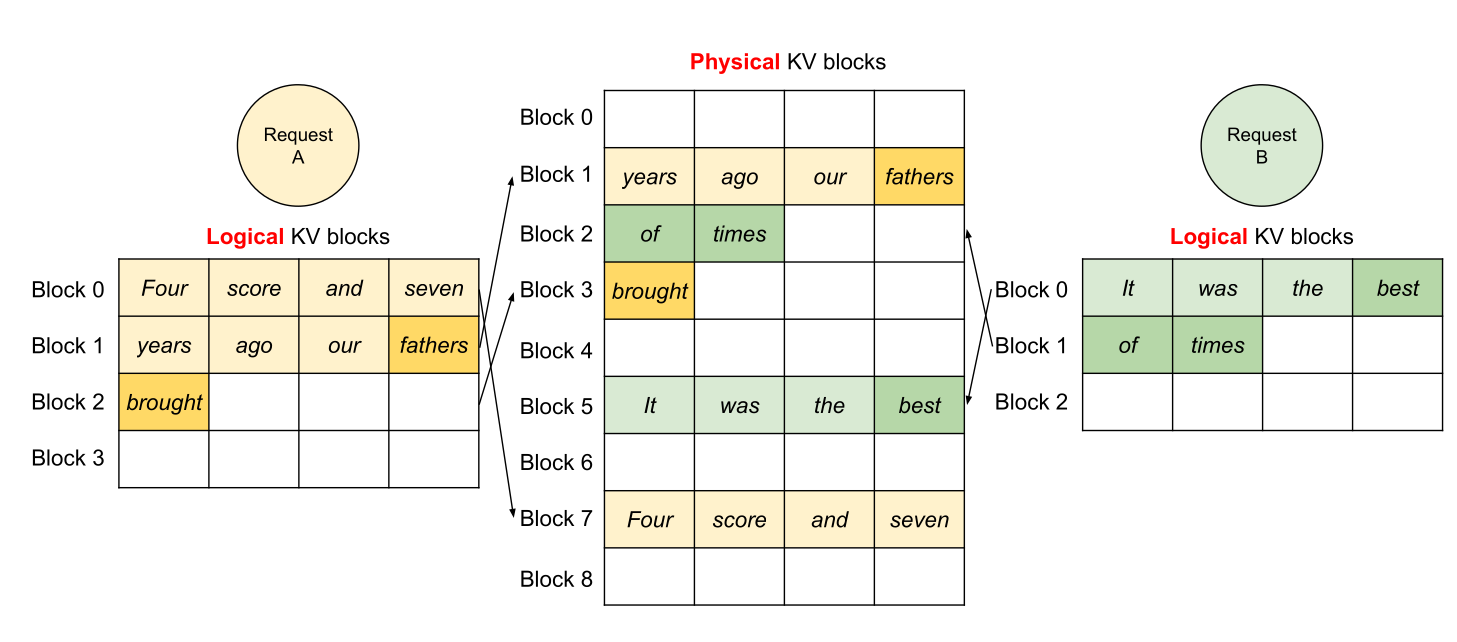
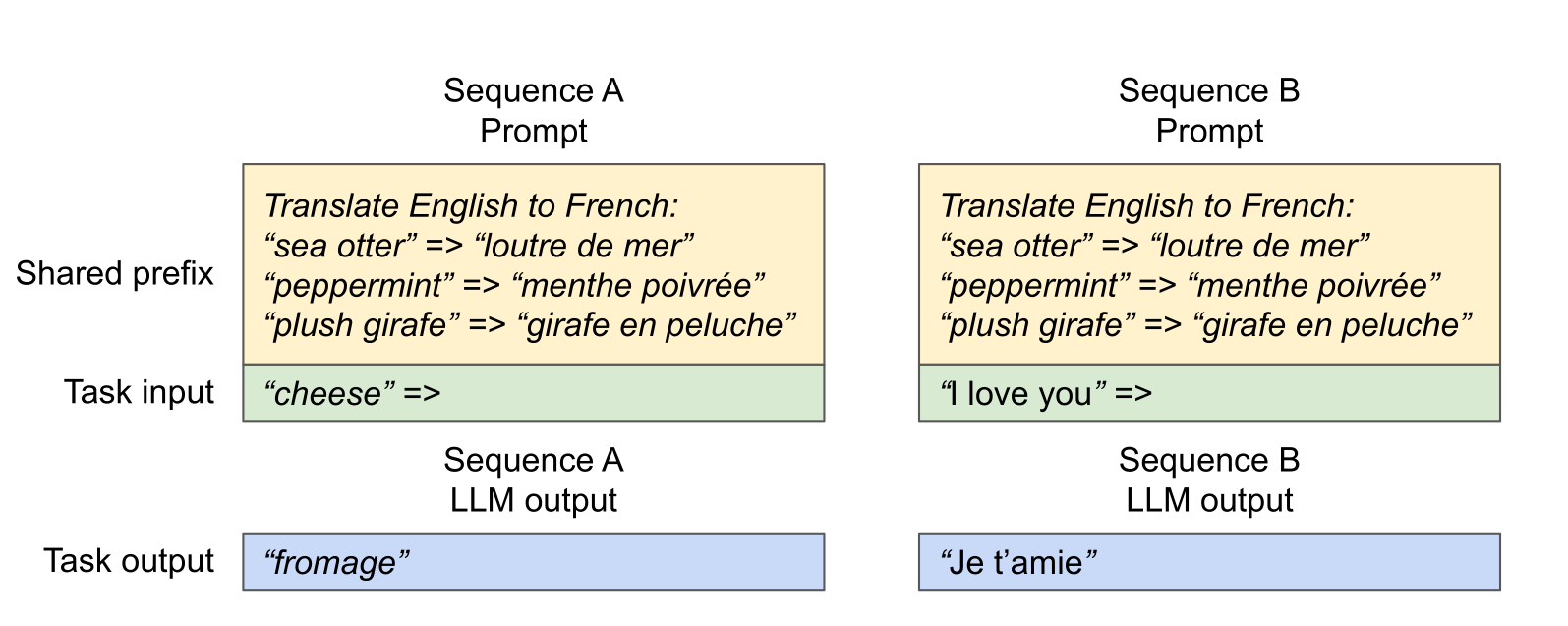
额外红利：更容易做 共享前缀（copy-on-write），例如：

• 多请求共享同一段 system prompt
• best-of-N 并行采样共享同一段 prefix

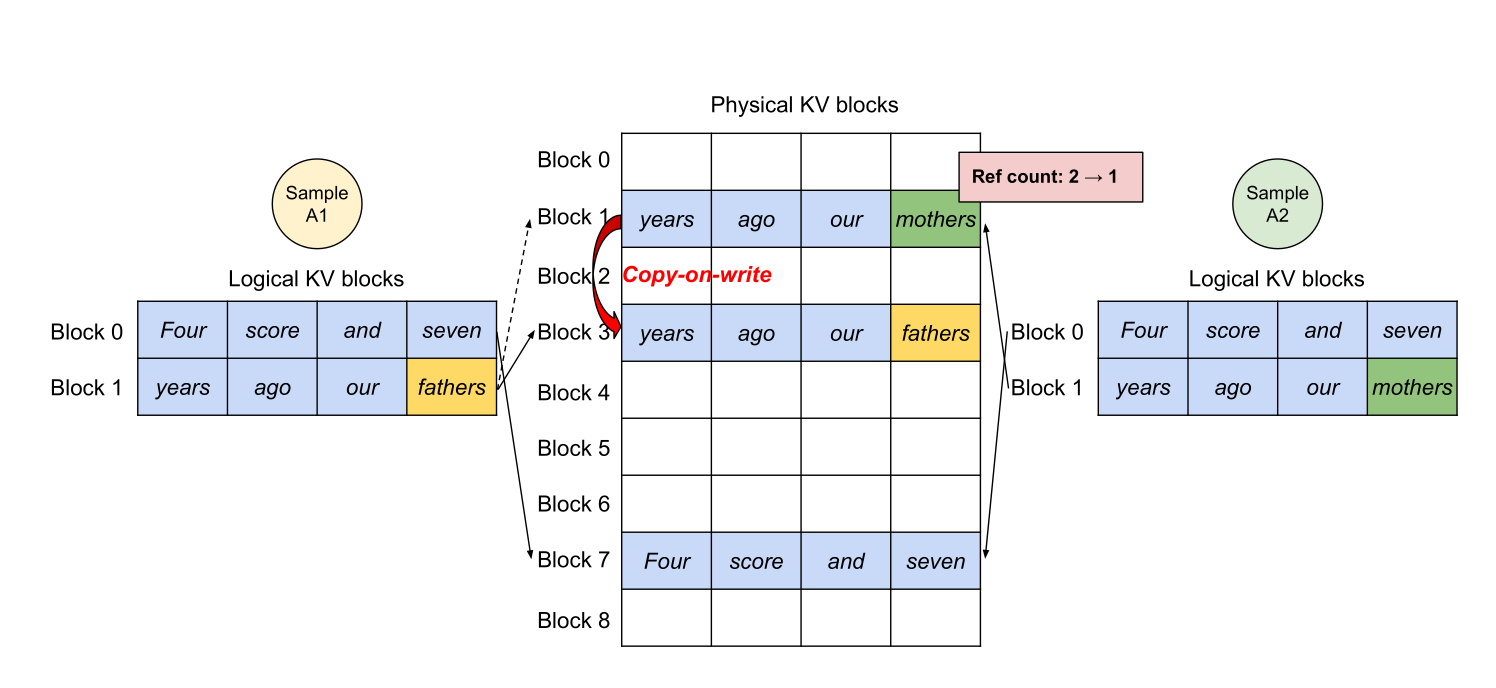
参考：https://github.com/vllm-project/vllm（以及相关论文/实现）

9. Decode 步数变少：Speculative Decoding（投机采样）

前面两条路线本质都在和“带宽墙”较劲：要么少读一点（瘦身/复用），要么把读的成本摊薄到更多并发上（调度）。投机解码换了一条思路：不改变单步 decode 的带宽属性，而是直接减少需要走的步数。

投机解码利用一个不对称性：

“验证一段 token（并行）”通常比“生成这段 token（串行）”更快。

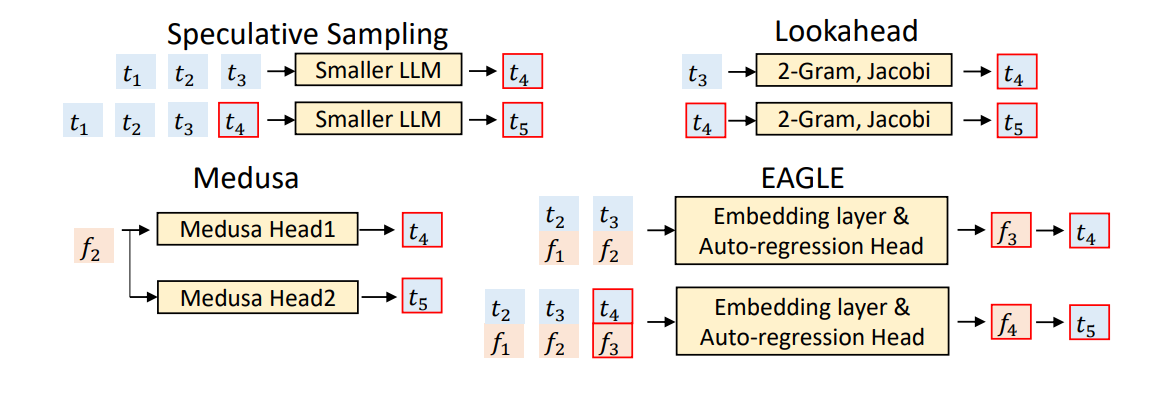
流程（草图）：

1. 用小模型（draft，分布 p）快速生成接下来 K 个 token
2. 用大模型（target，分布 q）一次前向并行计算这 K 步的分布
3. 逐步做 accept/reject：接受的 token 直接“白嫖”，一旦拒绝则按残差分布修正

关键性质：在合适的 accept/reject 规则下，最终输出分布严格等于 q（无损）。直觉上可以理解为“多退少补”：

• draft 过采样的 token 会以概率 q/p 被拒掉一部分（削峰）
• draft 欠采样的 token 会从残差 max(q-p,0) 中补回来（填谷）

工程变体（方向感）：

• Medusa：不再引入独立小模型，而是在大模型上加多个预测头一次预测多步
• EAGLE：让 draft 读取大模型中间特征，提高命中率

10. 替代 Transformer 的方向

如果把目标定为“彻底摆脱 decode 的内存墙/串行墙”，那就会出现“替代架构”。

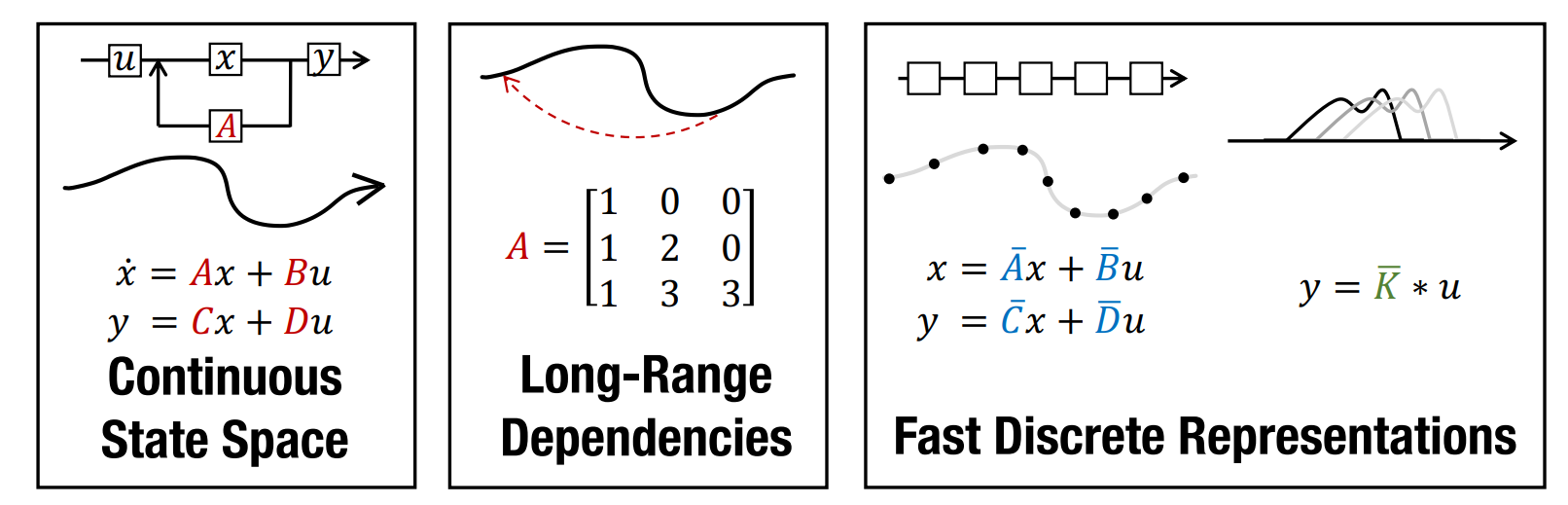
10.1 状态空间模型（SSM）/ Mamba 系列

直觉：把历史压成固定大小的状态，推理内存从 O(S) 变为 O(1)，长文本生成更友好。

• S4 → 长序列合成任务强，但语言的“回忆/检索”能力弱
• Mamba → 引入输入依赖的选择机制，1B 规模能对齐 Transformer 质量且推理很快
• Jamba → Transformer + Mamba 混合（再叠 MoE），体现“混合可能是赢家”

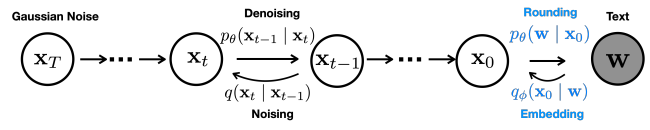
10.2 Diffusion（文本扩散/并行生成）

思路：非自回归，不是一词一词蹦，而是多轮迭代并行“去噪”整段文本；在某些结构化任务（如代码）可能非常快。

小结：把优化手段对齐到瓶颈

• Prefill（更像 compute-bound）：重点是算子融合、并行策略、提高 GEMM 利用率（本文主要把它当作“背景对照”）。
• Decode（更像 memory-bound）：重点是减少 HBM 搬运与降低 KV 成本：GQA/MQA/MLA/CLA/local → “KV 变小/变短/变共享”。
• 吞吐不浪费：Continuous batching 解决“请求不齐导致 batch 不稳”，PagedAttention 解决“KV 分配与碎片”。
• 步数更少：Speculative decoding 用“并行验证”替代“串行生成”的一部分，直接提升 tokens/s。

参考读

• Transformer 结构回顾（Scaling Book）：https://jax-ml.github.io/scaling-book/transformers/
• GQA：https://arxiv.org/pdf/2305.13245
• MLA：https://arxiv.org/abs/2405.04434
• CLA：https://arxiv.org/abs/2405.12981
• Longformer（local + global attention）：https://arxiv.org/abs/2004.05150
• vLLM / PagedAttention：https://github.com/vllm-project/vllm