TP 并行的通讯计算

张量并行（Tensor Parallelism, TP）就是为了处理“大权重”。

然而，TP 并非免费的午餐。它的核心矛盾在于：通过切分矩阵降低了显存消耗，却引入了极高频率的计算内通信。

1. 权重的切分（通信算子的引入）

张量并行的核心是将线性层 $Y = XW$ 进行切分。根据切分方向的不同，引入了不同的通信算子。

1.1 列并行 (Column Parallelism)

列并行将线性层的输出维度切开：把权重 $W$ 按列切分为 \(W = [W_1, W_2]\) 于是每块 GPU 只负责产出一段输出特征： \(Y = XW = [XW_1, XW_2] = [Y_1, Y_2]\)

1.1.1 Forward

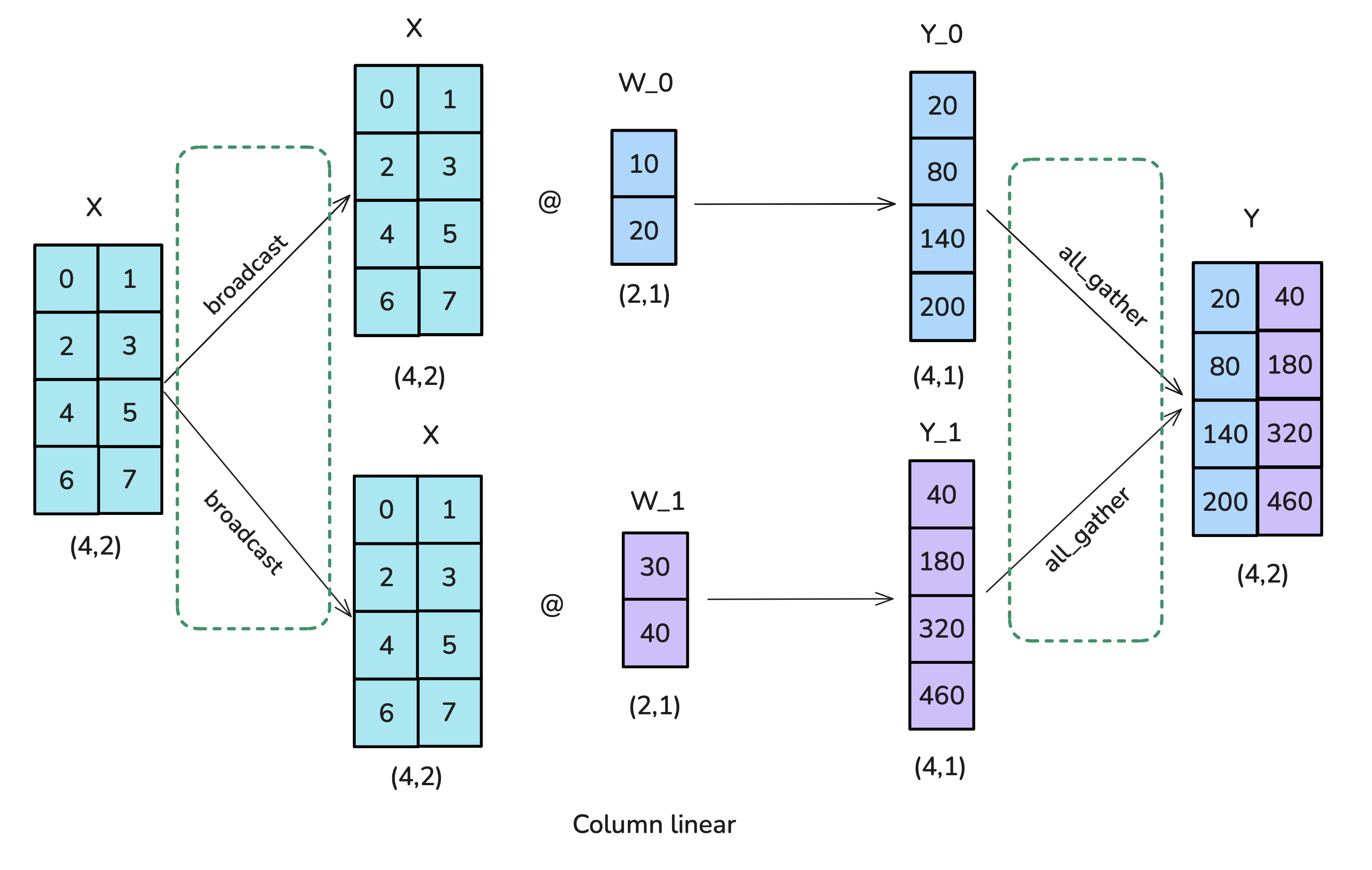为了方便理解，我们同样假设有 2 块 GPU：

中间计算

• GPU1 计算 $Y_1 = XW_1$
• GPU2 计算 $Y_2 = XW_2$
• 此时每块 GPU 只持有局部输出（输出特征的一部分）。

通信算子 $g$

• 触发条件： 如果后续算子需要完整的 $Y$（例如残差相加、LayerNorm，或任何不做 TP 切分的算子）。
• 动作： 全聚合 (All-Gather / Concat)
• 过程： 收集各卡的 $Y_i$ 并按特征维拼接。
• 结果： \(Y = \mathrm{AllGather}([Y_1, Y_2]) = [Y_1, Y_2]\)

1.1.2 Backward

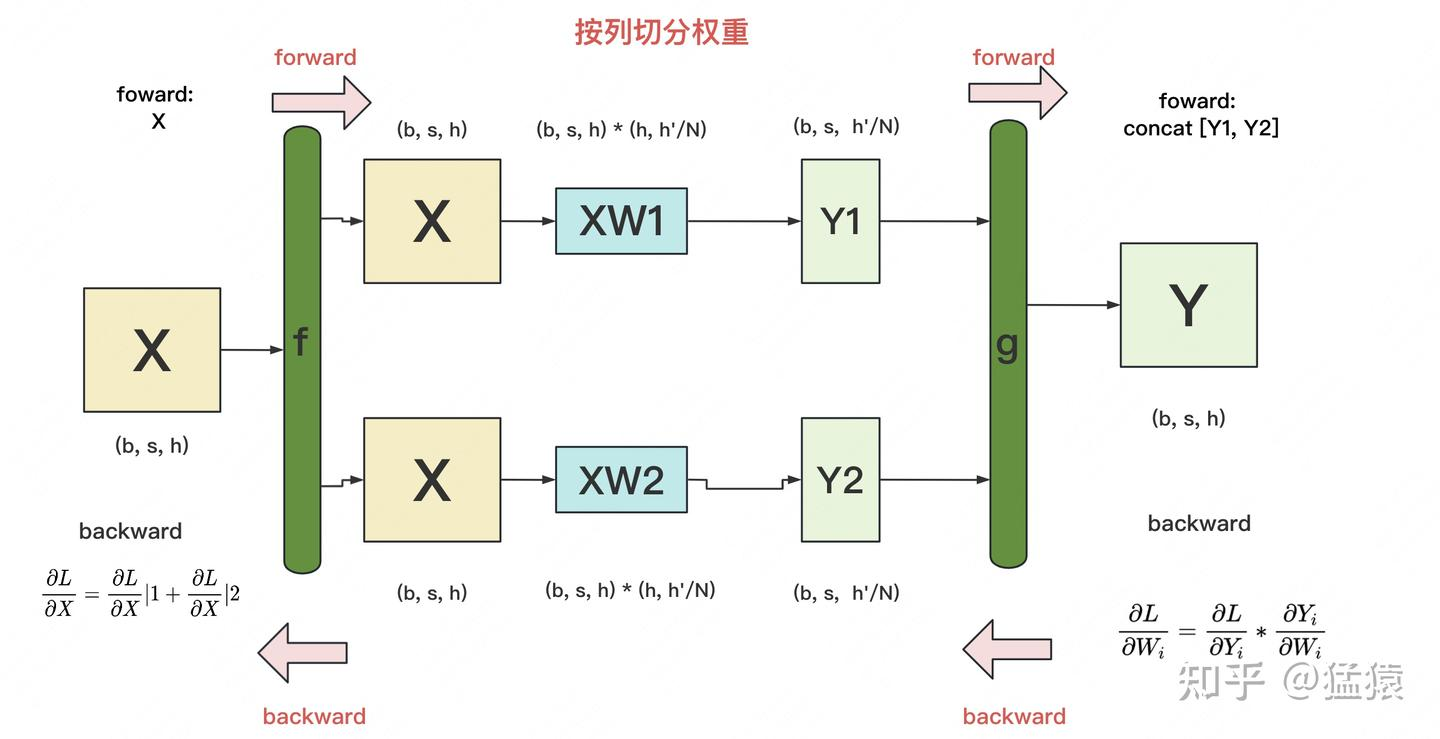
在列并行里，每块 GPU 只负责输出维度的一段：

• 计算：每个 GPU 持有 $W_i$，计算局部输出 $Y_i = XW_i$。
• 前向（All-Gather）：如果后续算子需要完整的输出（例如要做残差相加、LayerNorm 等），就需要把各卡的局部输出拼起来： \(Y = \mathrm{AllGather}([Y_1, Y_2]) = [Y_1, Y_2]\)

为什么 All-Gather 的反向是 Reduce-Scatter？

关键在于：All-Gather 会让“完整的 $Y$”出现在每一块 GPU 上，而后续计算通常是并行分摊在各个 GPU 上进行的，因此每块 GPU 都会产生一份对 $Y$ 的梯度贡献。设第 $r$ 块 GPU 在后续计算得到的损失为 $L^{(r)}$，总损失为： \(L = \sum_r L^{(r)}\) 那么对 $Y$ 的梯度是把各卡的贡献相加： \(\frac{\partial L}{\partial Y} = \sum_r \frac{\partial L^{(r)}}{\partial Y}\) 而我们真正希望回传给列并行线性层的是各卡对应的那一片 $\frac{\partial L}{\partial Y_i}$（因为 $Y_i$ 是本卡算出来的局部输出）。因此需要两步合在一起做：

1. Reduce（Sum）：把所有 GPU 上的 $\frac{\partial L^{(r)}}{\partial Y}$ 按元素求和，得到全局的 $\frac{\partial L}{\partial Y}$。
2. Scatter：再把这个全局梯度按列并行的切分方式切开，取回每块 GPU 自己负责的那一段 $\frac{\partial L}{\partial Y_i}$。

这就是 Reduce-Scatter：把“求和”和“切分返还”融合成一次通信

1.1.3 代码实现

https://github.com/NVIDIA/Megatron-LM/blob/core_v0.15.0/megatron/core/tensor_parallel/layers.py#L743

1. 权重预先切分：ColumnParallelLinear.__init__ 把权重形状 [out_features, in_features] 按输出维（dim0）等分成 output_size_per_partition = output_size / tp_world_size，每个 rank 只持有一块 A_i（对应部分输出列）。bias同维度切分。

2. 前向不再切输入：保持完整输入 X（除非 sequence-parallel/显式 MoE 已分好），直接用本 rank 的权重块做 Y_i = X @ A_i^T，得到局部输出列块。

3. 输出是否合并：如果需要完整输出，末尾 gather_from_tensor_model_parallel_region 把各 rank 的 Y_i 拼成全量 Y；否则保持分片，便于后续仍在 TP 下继续算。

1.2 行并行（Row parallelism）

按照输入维度进行切分

1.2.1 Forward

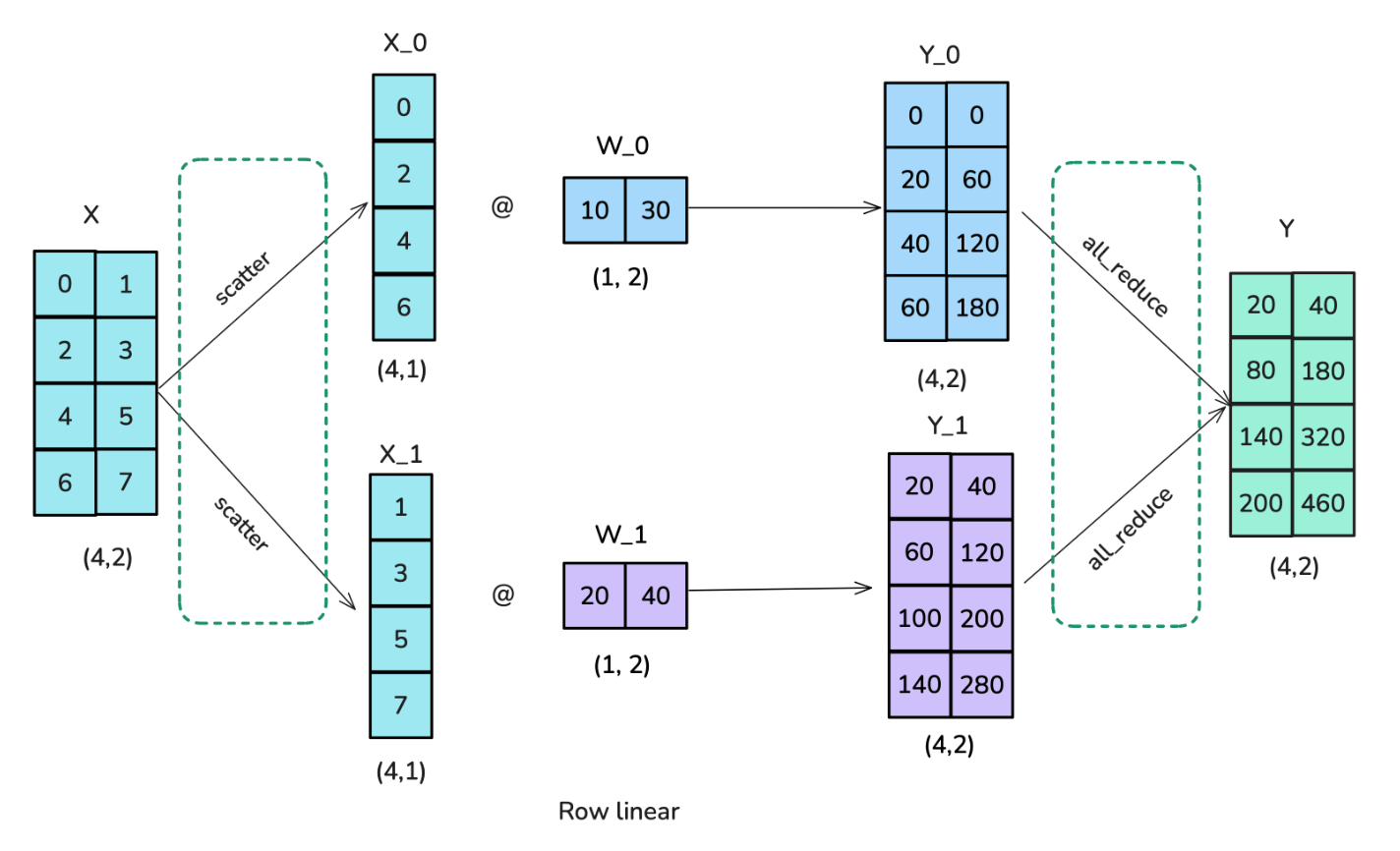
算子 $f$

• 动作： 切分 (Split)
• 过程： 完整的输入张量 $X$ 进入 $f$。由于权重 $W$ 是按行切分的，为了满足矩阵乘法规则，输入 $X$ 必须按列切分。
• 结果： $f$ 把 $X$ 拆成了 $[X_1, X_2]$。
  • $X_1$ 发给 GPU1。
  • $X_2$ 发给 GPU2。

中间计算

• GPU1 计算 $Y_1 = X_1 W_1$
• GPU2 计算 $Y_2 = X_2 W_2$
• 此时，每块 GPU 上都只拿着结果的一段（局部求和项）。

算子 $g$

• 动作： 全规约 (All-Reduce / Sum)
• 过程： $g$ 把 GPU1 的 $Y_1$ 和 GPU2 的 $Y_2$ 加起来。
• 结果： 得到 $Y = Y_1 + Y_2$。
  • 执行完 $g$ 后，两块 GPU 都能拿到完整的输出结果 $Y$，供下一层网络使用。

1.2.2 Backward

反向传播的方向是：$\frac{\partial L}{\partial Y} \rightarrow g \rightarrow \text{求导} \rightarrow f \rightarrow \frac{\partial L}{\partial X}$

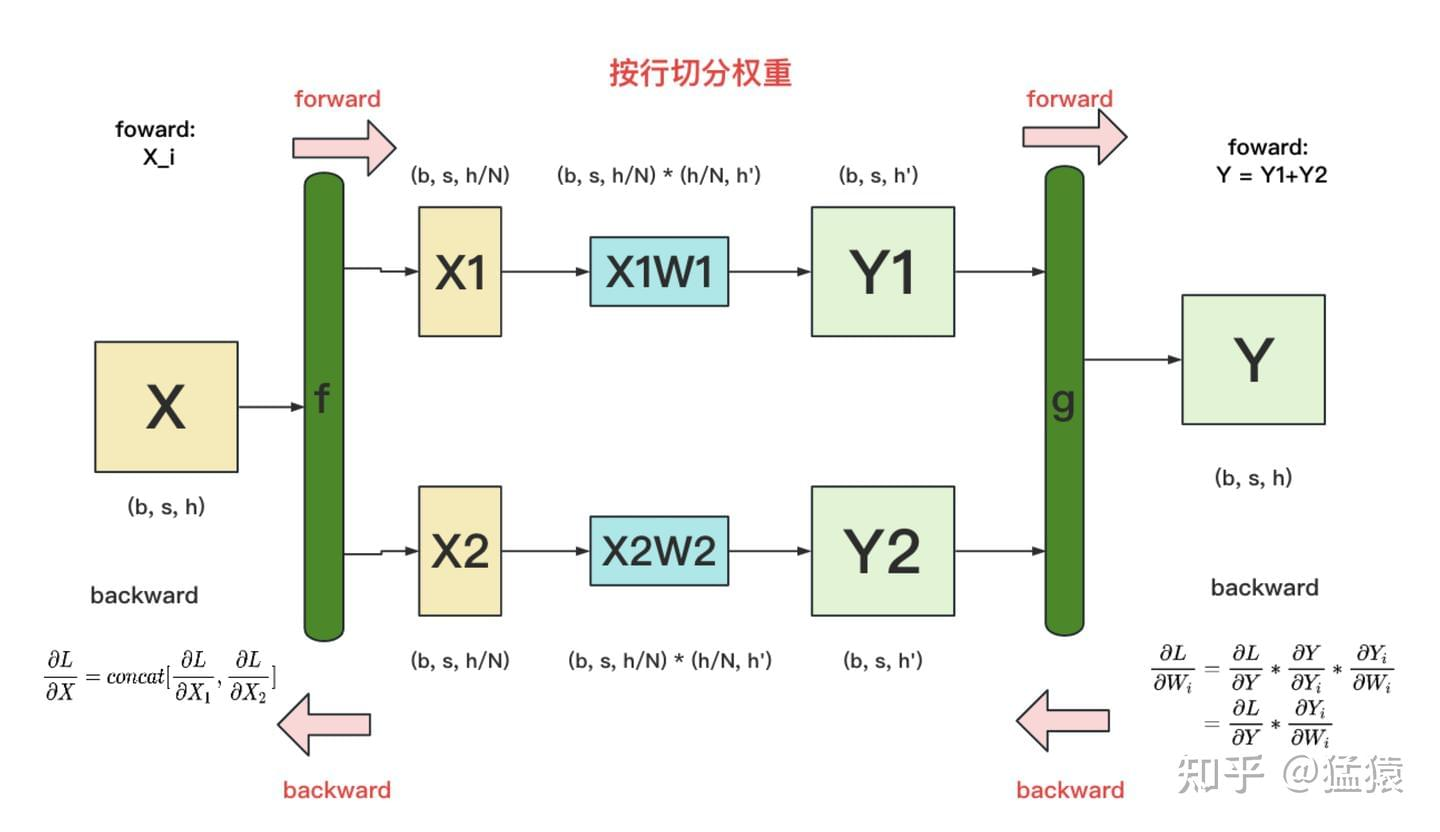
1.2.2.1 算子 $g$

• 动作： 恒等映射 / 复制 (Identity / Copy)
• 过程： 上一层传回了总输出的梯度 $\frac{\partial L}{\partial Y}$。
• 原理： 因为前向是 $Y = Y_1 + Y_2$，根据加法的求导法则，偏导数直接传递：$\frac{\partial L}{\partial Y_1} = \frac{\partial L}{\partial Y}$ 且 $\frac{\partial L}{\partial Y_2} = \frac{\partial L}{\partial Y}$。
• 结果： $g$ 把同样的梯度 $\frac{\partial L}{\partial Y}$ 直接复制一份，分别分发给两条支路

1.2.2.2 中间求导计算

• 每块 GPU 根据自己手里的 $X_i, W_i$ 和传回的梯度计算：
  • 权重的梯度：$\frac{\partial L}{\partial W_1}$ 和 $\frac{\partial L}{\partial W_2}$（局部更新）。
  • 输入的梯度：$\frac{\partial L}{\partial X_1}$ 和 $\frac{\partial L}{\partial X_2}$。

1.2.2.3 算子 $f$

• 动作： 聚合 (All-Gather / Concat)
• 过程： $f$ 收集 GPU1 产生的 $\frac{\partial L}{\partial X_1}$ 和 GPU2 产生的 $\frac{\partial L}{\partial X_2}$。
• 结果： 将它们拼接回完整的梯度 $\frac{\partial L}{\partial X}$。
  • 这样，梯度就能以完整的形态传回给更早之前的网络层了。

1.2.3 代码实现

https://github.com/NVIDIA/Megatron-LM/blob/core_v0.15.0/megatron/core/tensor_parallel/layers.py#L1068

1. 参数切分方式：权重形状 [out_features, in_features_per_rank]，在构造时按输入维（dim1）均分，偏置不分片。也就是说每个 rank 只存自己负责的输入行块。
2. 输入处理：
   • 如果 input_is_parallel=True，认为输入已按最后一维切好；否则在 forward 开头用 scatter_to_tensor_model_parallel_region 把完整输入按隐藏维分给各 rank。
   • 开启 sequence parallel 时要求输入已分好（input_is_parallel=True）。
3. 局部计算：本 rank 做 X_i @ W_i^T，得到局部输出块 Y_i，没有偏置。
4. 输出聚合：
   • MoE 显式通信时直接返回分片输出（要求 skip_bias_add）。
   • 若 sequence_parallel=True，用 reduce_scatter_to_sequence_parallel_region；否则用 reduce_from_tensor_model_parallel_region 对所有 rank 的 Y_i 求和（相当于全量 matmul 结果）。
5. 加偏置：如果 skip_bias_add=False，在当前 rank 加全量偏置并返回 (output, None)；否则返回 (output, bias) 让上游融合。 目的：通过按输入维切分权重/输入，减少每个 rank 的参数和计算；输出端用 reduce 聚合回完整输出，或在 MoE/sequence parallel 场景下保持/组合分片以继续并行。文件参考：

如果每一层矩阵乘法都做一次 All-Reduce，通信开销将淹没计算。Megatron-LM 提出了一种巧妙的组合方式，将两个线性层串联，把通信合并。

简单理解：

行切分需要切输入，列切分需要切输出

列切分会把输出维度切开，这时候不做all reduce ，把前面的切好的列切分的输出当成行切分的输入

省去2层之间的通信

2. MLP 层的TP切分

2.1 TP切分

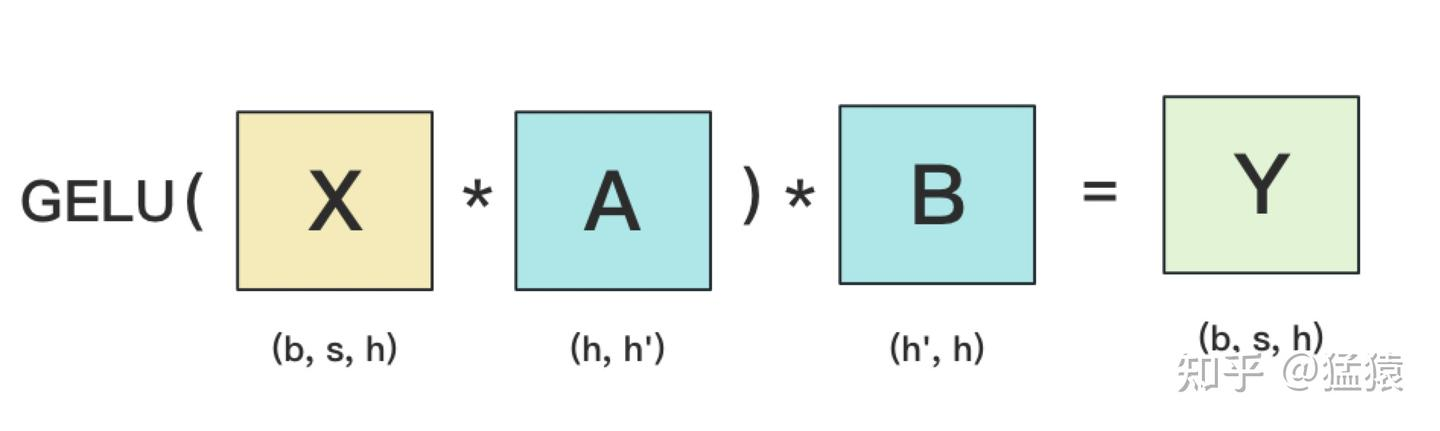
其中GELU 是激活函数，AB分别表示2个线性层

Transformer 里，一般 h’ = 4h

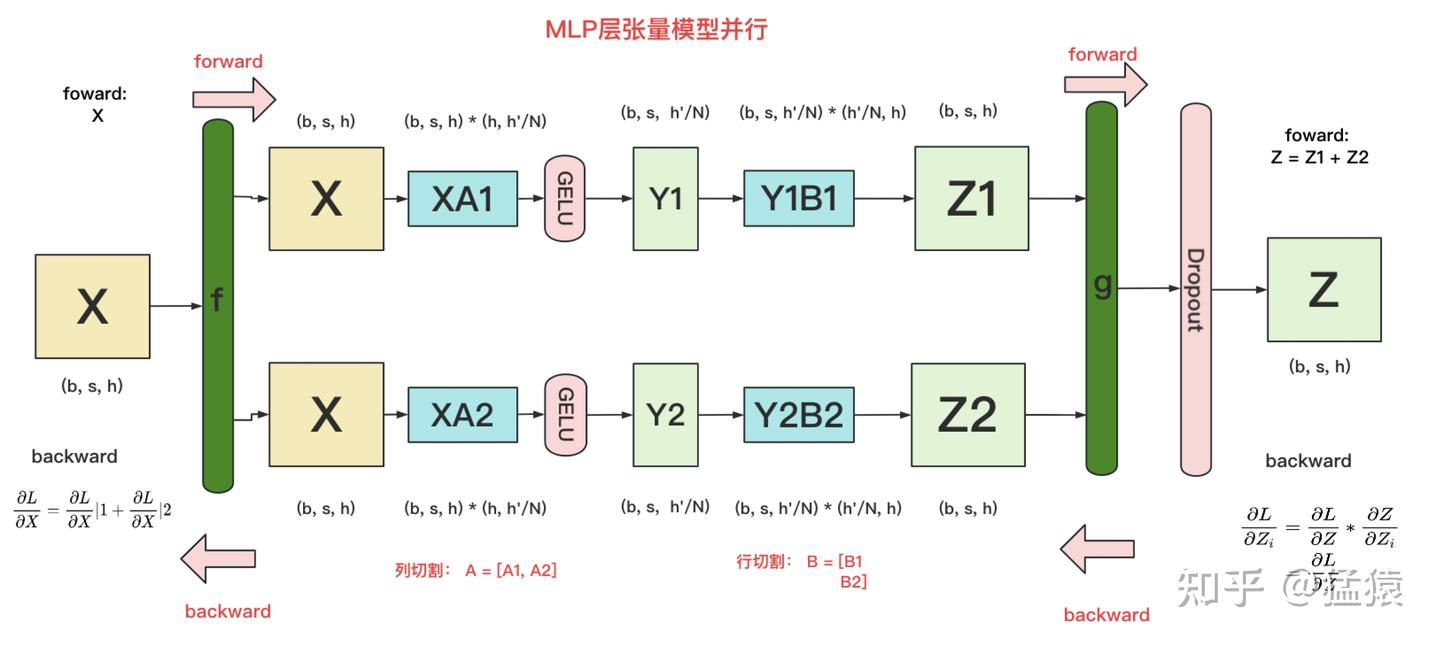
在MLP层中，对A采用”列切割”，对B采用”行切割”。

• f 的forward计算：把输入X拷贝到两块GPU上，每块GPU即可独立做forward计算。

• g 的forward计算：每块GPU上的forward的计算完毕，取得Z1和Z2后，GPU间做一次AllReduce，相加结果产生Z。

• g 的backward计算：只需要把 $\frac{\partial L}{\partial Z}$ 拷贝到两块GPU上，两块GPU就能各自独立做梯度计算。

• f 的backward计算：当当前层的梯度计算完毕，需要传递到下一层继续做梯度计算时，我们需要求得 $\frac{\partial L}{\partial X}$。则此时两块GPU做一次AllReduce，把各自的梯度 $\frac{\partial L}{\partial X}

  1$ 和 $\frac{\partial L}{\partial X}

  2$ 相加即可。

为什么我们对A采用列切割，对B采用行切割呢？这样设计的原因是，我们尽量保证各GPU上的计算相互独立，减少通讯量。对A来说，需要做一次GELU的计算，而GELU函数是非线性的，它的性质如下：

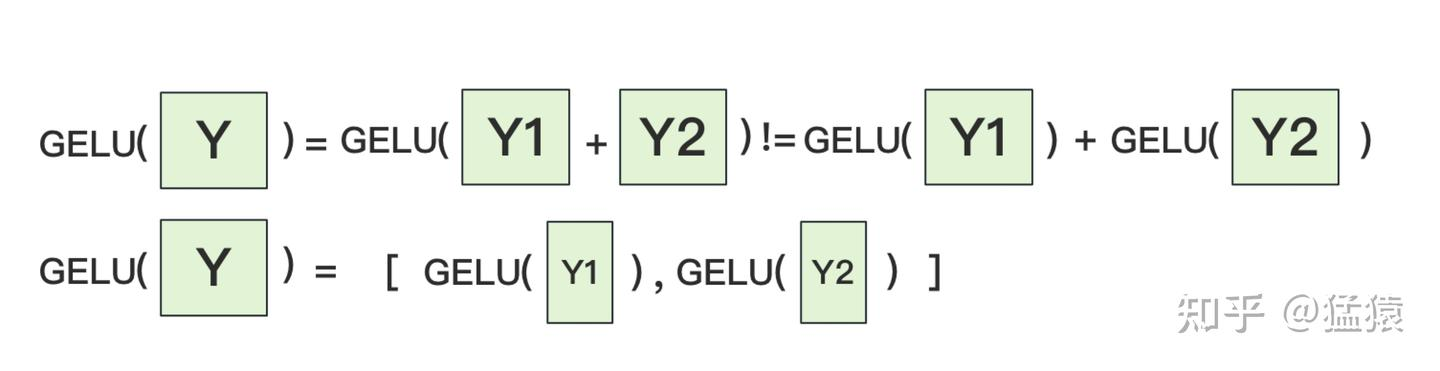
也就意味着，如果对A采用行切割，我们必须在做GELU前，做一次AllReduce，这样就会产生额外通讯量。但是如果对A采用列切割，那每块GPU就可以继续独立计算了。一旦确认好A做列切割，那么也就相应定好B需要做行切割了

2.2 通信量分析

由2.1的分析可知，MLP层做forward时产生一次AllReduce，做backward时产生一次AllReduce。

AllReduce的过程分为两个阶段，Reduce-Scatter和All-Gather，每个阶段的通讯量都相等。现在我们设每个阶段的通讯量为 $\Phi$，

则一次AllReduce产生的通讯量为 $2\Phi$。MLP层的总通讯量为 $4\Phi$。

根据上面的计算图，我们也易知，$\Phi = b * s * h$

2.3 优化点

1. GELU(XW₁)：$W_1$ 使用列并行（按输出维 $h’$ 切分）。因此 $XW_1$ 的输出天然是分片的；GELU/Dropout 等逐元素算子可在分片上独立计算，无需 All-Gather，可直接将分片送入下一层。
2. (Dropout ∘ GELU)(XW₁) · W₂：$W_2$ 使用行并行（按输入维 $h’$ 切分）。每张卡得到的是输出的部分和，在第二个线性层输出处触发一次 All-Reduce 得到完整结果。
   • 结果（FWD）：两次矩阵乘法，中间不做 All-Gather，仅在第二层输出处进行 1 次 All-Reduce。
   • 结果（BWD）：回传到上一层时，$\frac{\partial L}{\partial X}$ 是各卡的部分和，需要再做 1 次 All-Reduce 聚合；除此之外无需额外通信。
   • 意义：利用「列并行 → 逐元素 → 行并行」的张量布局可直接衔接，避免中间把激活还原为全量张量的通信；相较于“每个线性层后都同步一次”的朴素实现，通信频率约降低 50%（以 forward 为例从 2 次降为 1 次）。

2.4 MLP 切分实现

https://github.com/NVIDIA/Megatron-LM/blob/core_v0.15.0/megatron/core/transformer/mlp.py#L58

1. 切分方式：
   • linear_fc1 默认用 ColumnParallelLinear（通过 build_module 注入，见 MLP.init），权重按输出维切分，每个 rank 产出自己那份中间激活；gather_output=False，所以保持分片。
   • 激活在各自 rank 上就地执行（可融合 bias/激活）。
   • linear_fc2 默认用 RowParallelLinear，按输入维切分，输入认为已分片，输出端做 reduce/reduce-scatter 得到全量或分片结果。
2. 结构
   • 标准 FFN，两层线性 + 激活。linear_fc1 把输入从 hidden_size 投到 ffn_hidden_size（GLU 时翻倍），linear_fc2 再投回 hidden_size

具体指定：

https://github.com/NVIDIA/Megatron-LM/blob/core_v0.15.0/megatron/core/models/gpt/gpt_layer_specs.py#L366

    linear_fc2 = backend.row_parallel_linear()
    activation_func = backend.activation_func() if use_te_activation_func else None

    if num_experts is None:
        # Dense MLP w/ or w/o TE modules.
        module = TEFusedMLP if use_te_op_fuser else MLP
        if backend.fuse_layernorm_and_linear():
            linear_fc1 = backend.column_parallel_layer_norm_linear()
            assert linear_fc1 is not None
        else:
            linear_fc1 = backend.column_parallel_linear()

3. Self-Attn /MHA 层

3.1 MHA的计算

3.1.1 head=1

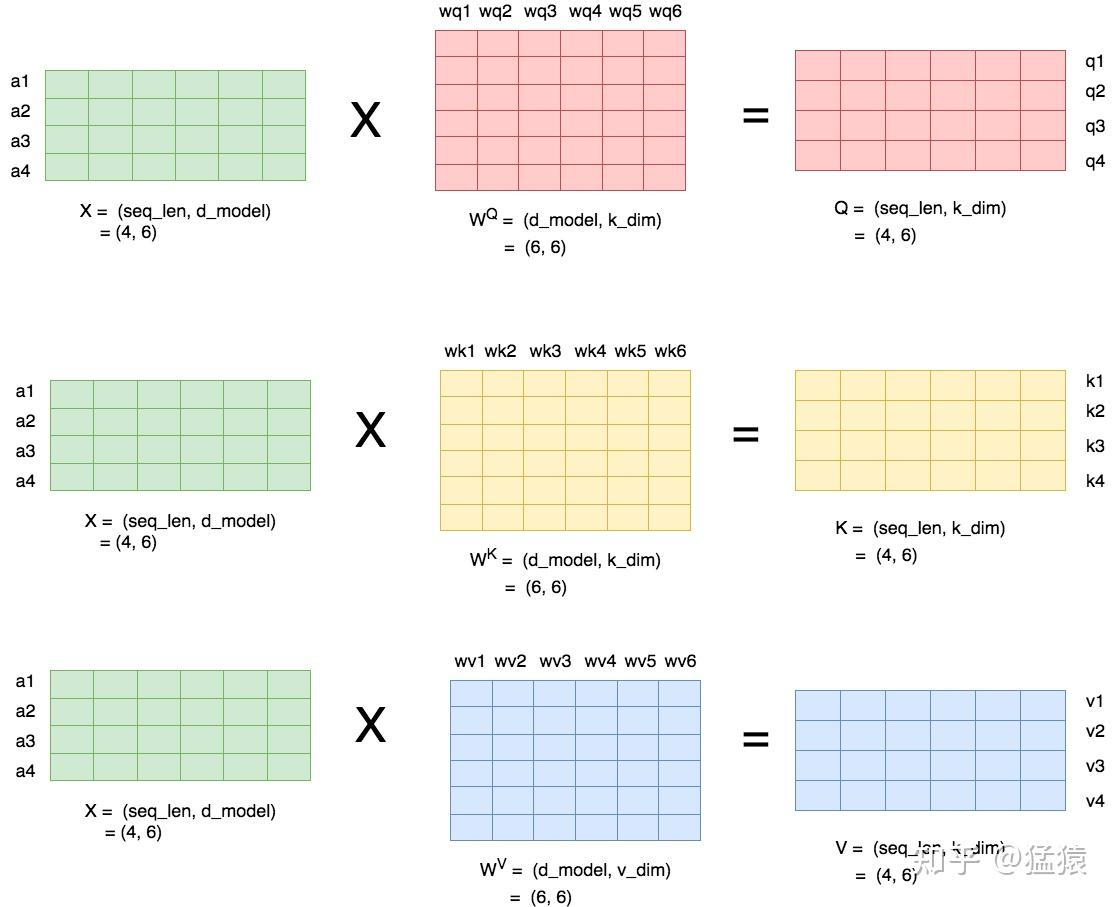
• seq_len，d_model即序列长度和每个token的向量维度
• $W^Q, W^K, W^V$ 即attention层需要做训练的三块权重。

• k_dim，v_dim满足：

  $k_dim = v_dim = d_model//num_heads = h//num_heads$

3.1.2 多头

理清了单头，我们来看多头的情况，下图展示了当num_heads = 2时attention层的计算方法。即对每一块权重，我们都沿着列方向（k_dim）维度切割一刀。此时每个head上的 $W^Q, W^K, W^V$ 的维度都变成(d_model, k_dim//2)。每个head上单独做矩阵计算，最后将计算结果concat起来即可。整个流程如下：

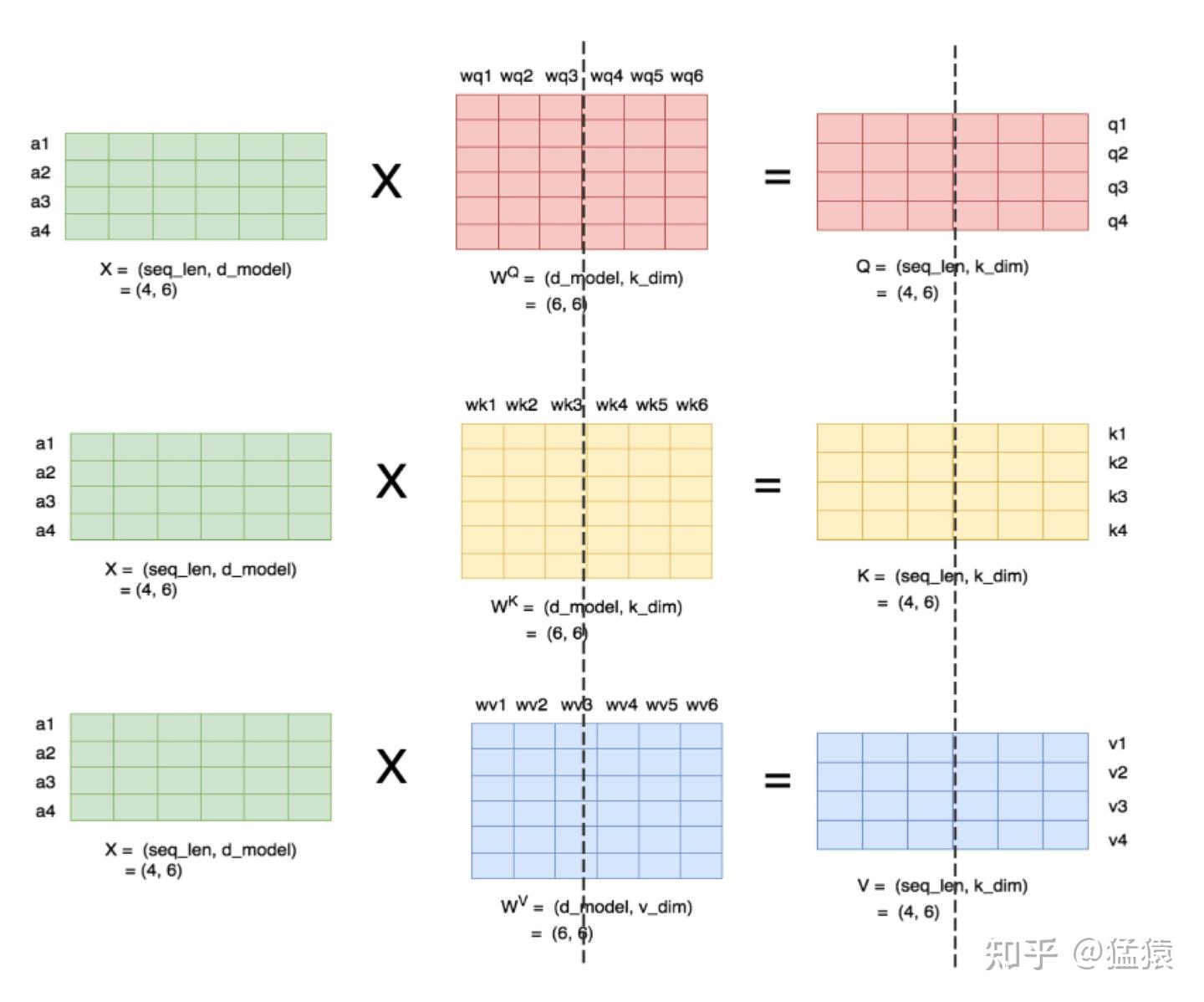
可以发现，attention的多头计算简直是为张量模型并行量身定做的，因为每个头上都可以独立计算，最后再将结果concat起来。也就是说，可以把每个头的参数放到一块GPU上。则整个过程可以画成：

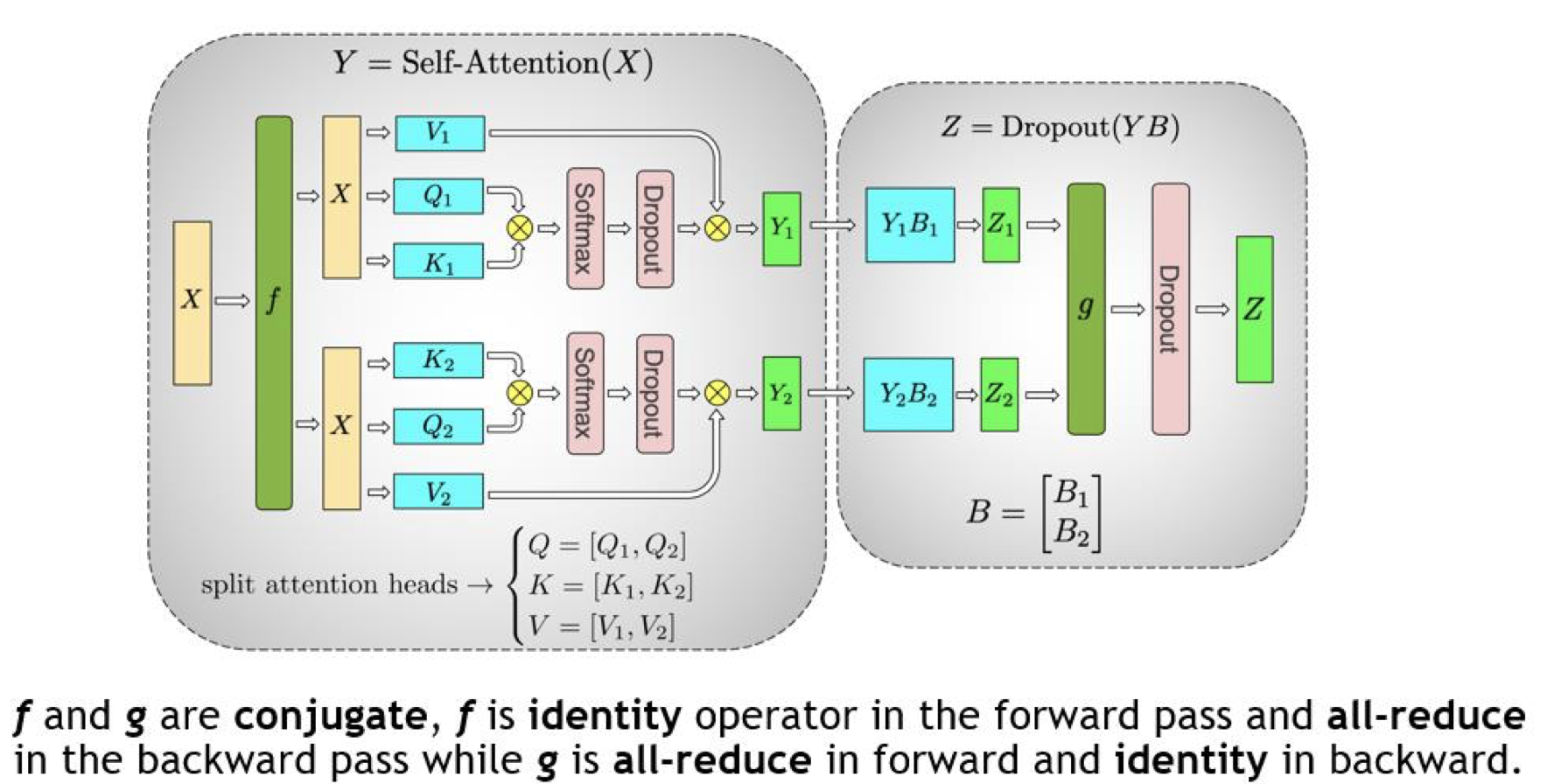
左半部分：$Y = \text{Self-Attention}(X)$ (列并行)

• 权重切分： 用于生成 Query ($Q$), Key ($K$), Value ($V$) 的线性层的权重矩阵被按列切分。
  • $Q$ 被切分为 $[Q_1, Q_2]$，分别放在 GPU 1 和 GPU 2 上。$K$ 和 $V$ 同理。
  • 这意味着每个 GPU 负责处理一部分注意力头（Heads）。图中 GPU 1 处理 Head 1，GPU 2 处理 Head 2。
• 计算过程： 每个 GPU 独立计算自己负责的那部分注意力的输出（$Y_1$ 和 $Y_2$）。
• 通信状态 ($f$)： 在前向传播中，$f$ 是 Identity（恒等算子）。这意味着输入的 $X$ 在每个 GPU 上都是完整的副本，GPU 之间不需要交换数据即可开始计算各自的头。

右半部分：$Z = \text{Dropout}(YB)$ (行并行)

• 权重切分： 注意力机制最后的输出投影层（Output Projection）权重 $B$ 被按行切分，即 $B = \begin{bmatrix} B_1 \ B_2 \end{bmatrix}$。
• 计算过程：
  • GPU 1 计算 $Z_1 = Y_1 B_1$。
  • GPU 2 计算 $Z_2 = Y_2 B_2$。
  • 根据矩阵乘法原理：$Z = YB = [Y_1, Y_2] \begin{bmatrix} B_1 \ B_2 \end{bmatrix} = Y_1 B_1 + Y_2 B_2 = Z_1 + Z_2$。
• 通信状态 ($g$)： 为了得到最终的输出 $Z$，必须将两个 GPU 上的部分结果 $Z_1$ 和 $Z_2$ 相加。因此，在前向传播中，$g$ 是 All-Reduce（全归约） 算子。执行完 $g$ 后，每个 GPU 都拥有了完整的、求和后的 $Z$。

$f$ 和 $g$ 的共轭关系（通信逻辑:

底部文字是理解 TP 通信的关键。在深度学习框架中，为了保证梯度计算正确，前向和后向的通信算子是“共轭”的：

• 对于 $g$ (在输出端)：
  • 前向传播：All-Reduce。 求和汇总所有 GPU 的结果。
  • 后向传播：Identity。 梯度直接传回各自的路径，不需要额外通信。
• 对于 $f$ (在输入端)：
  • 前向传播：Identity。 输入 $X$ 直接进入计算。
  • 后向传播：All-Reduce。 因为在前向传播中，$X$ 被分发到了两个并行的分支，在反向传播时，来自这两个分支的关于 $X$ 的梯度需要通过 All-Reduce 进行累加汇总，以更新前一层。

优点：

1. 减少通信次数： 在整个 MHA 块中，只需要在最后进行一次 All-Reduce 通信 ($g$)。中间计算 $Q, K, V$ 以及注意力权重时，GPU 之间是完全独立的。
2. 显存优化： 所有的权重矩阵（$W_Q, W_K, W_V, W_{out}$）都分摊到了不同 GPU 上，极大降低了单个 GPU 的显存压力。
3. 负载均衡： 每个 GPU 负责相同数量的注意力头，计算量分布均匀。

对三个参数矩阵Q，K，V，按照“列切割”，每个头放到一块GPU上，做并行计算。对线性层B，按照“行切割”。切割的方式和MLP层基本一致，其forward与backward原理也一致

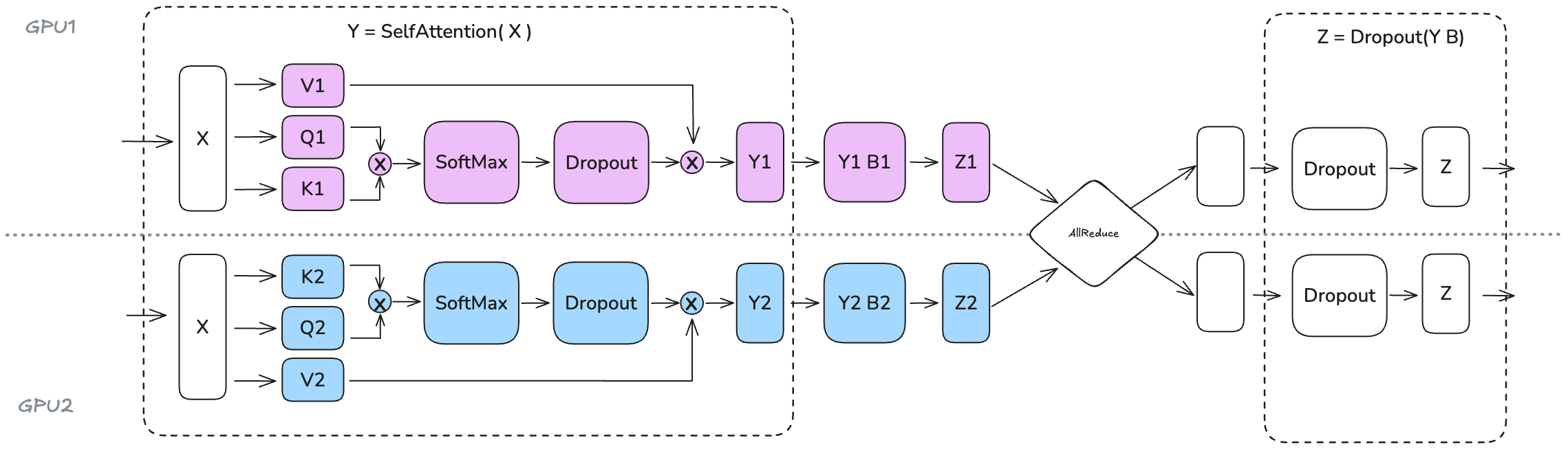
这张图，更直接描述TP下的数据流转

1. 完全独立的局部计算（紫色与蓝色区域） 从输入端开始，相同的输入张量 $X$ 被复制到两个 GPU 中。

• 空间隔离： GPU1（紫色）和 GPU2（蓝色）分别负责不同的注意力头（Attention Heads）。
• 零通信开销： 在生成 $Q, K, V$ 以及后续的 Softmax、Dropout 过程中，两个 GPU 之间没有任何数据交换。这意味着注意力机制中最耗时的“头计算”部分是完全并行的，计算效率随 GPU 数量线性增加。

2. 巧妙的线性投影切分（$Y_i B_i$ 阶段） 在 Self-Attention 输出后，紧接着是输出投影层（Output Projection）。

• 行切分（Row Parallel）： 注意力输出 $Y_1$ 和 $Y_2$ 并不需要先合并，而是直接与本地切分好的权重 $B_1$、$B_2$ 进行矩阵乘法。
• 得到部分和： 此时 GPU1 得到的是结果的一个“分量” $Z_1$，GPU2 得到的是 $Z_2$。

3. 唯一的同步关口：AllReduce 菱形算子 这是整张图的核心动线节点：

• 同步汇总： 为了得到最终正确的输出，图中央的 AllReduce 算子将 $Z_1$ 和 $Z_2$ 进行相加汇总。
• 状态还原： 经过这一次通信后，两个 GPU 重新获得了完全一致且完整的输出 $Z$。
• 极简设计： 这种设计保证了在整个复杂的 Attention 层计算中，跨 GPU 的通信仅发生这一次，极大地压低了分布式训练中的网络延迟。

总结：数据流的“沙漏型”特征 这张图揭示了 TP 并行的典型数据流特征：输入时完全一致（宽） $\rightarrow$ 计算过程中各算各的（分流） $\rightarrow$ 投影结束后通过 AllReduce 汇聚（窄） $\rightarrow$ 输出时再次回到一致状态（宽）。这种“分-合”结构正是 Megatron-LM 实现大规模模型高效并行的精髓所在。

最后，在实际应用中，并不一定按照一个head占用一块GPU来切割权重，我们也可以一个多个head占用一块GPU，这依然不会改变单块GPU上独立计算的目的。所以实际设计时，我们尽量保证head总数能被GPU个数整除。

3.2 通信量分析

类比于MLP层，self-attention层在forward中做一次AllReduce，在backward中做一次AllReduce。总通讯量也是 $4\Phi$。

3.3 Self-Attn 切分代码实现

https://github.com/NVIDIA/Megatron-LM/blob/core_v0.15.0/megatron/core/transformer/attention.py#L99

1. 切分构造

   • self.linear_qkv = build_module(submodules.linear_qkv, ...)，这里会实例化列并行的 QKV 权重并按输出维切分
   • self.linear_proj = build_module(submodules.linear_proj, ...)，这里会实例化行并行的输出投影，按输入维切分

2. 计算

   • 开头用 self.linear_qkv 做 QKV 投影（列并行，输出分片）。
   • 核心注意力算完后，结尾 output, bias = self.linear_proj(core_attn_out) 用行并行输出投影并聚合

至于具体指定，在 https://github.com/NVIDIA/Megatron-LM/blob/core_v0.15.0/megatron/core/models/gpt/gpt_layer_specs.py#L146

                    submodules=MLASelfAttentionSubmodules(
                        linear_q_proj=backend.column_parallel_linear(),
                        linear_q_down_proj=backend.linear(),
                        linear_q_up_proj=linear_q_up_proj,
                        linear_kv_down_proj=backend.linear(),
                        linear_kv_up_proj=linear_kv_up_proj,
                        core_attention=backend.core_attention(),
                        linear_proj=backend.row_parallel_linear(),
                        q_layernorm=IdentityOp,
                        kv_layernorm=IdentityOp,
                    ),

4. embeding 层

4.1 输入层

Embedding层一般由两个部分组成：

word embedding：维度(v, h)，其中v表示词表大小。 positional embedding：维度(max_s, h)，其中max_s表示模型允许的最大序列长度。

对positional embedding来说，max_s本身不会太长，因此每个GPU上都拷贝一份，对显存的压力也不会太大。但是对word embedding来说，词表的大小就很客观了，因此需要把word embedding拆分到各个GPU上，具体的做法如下：

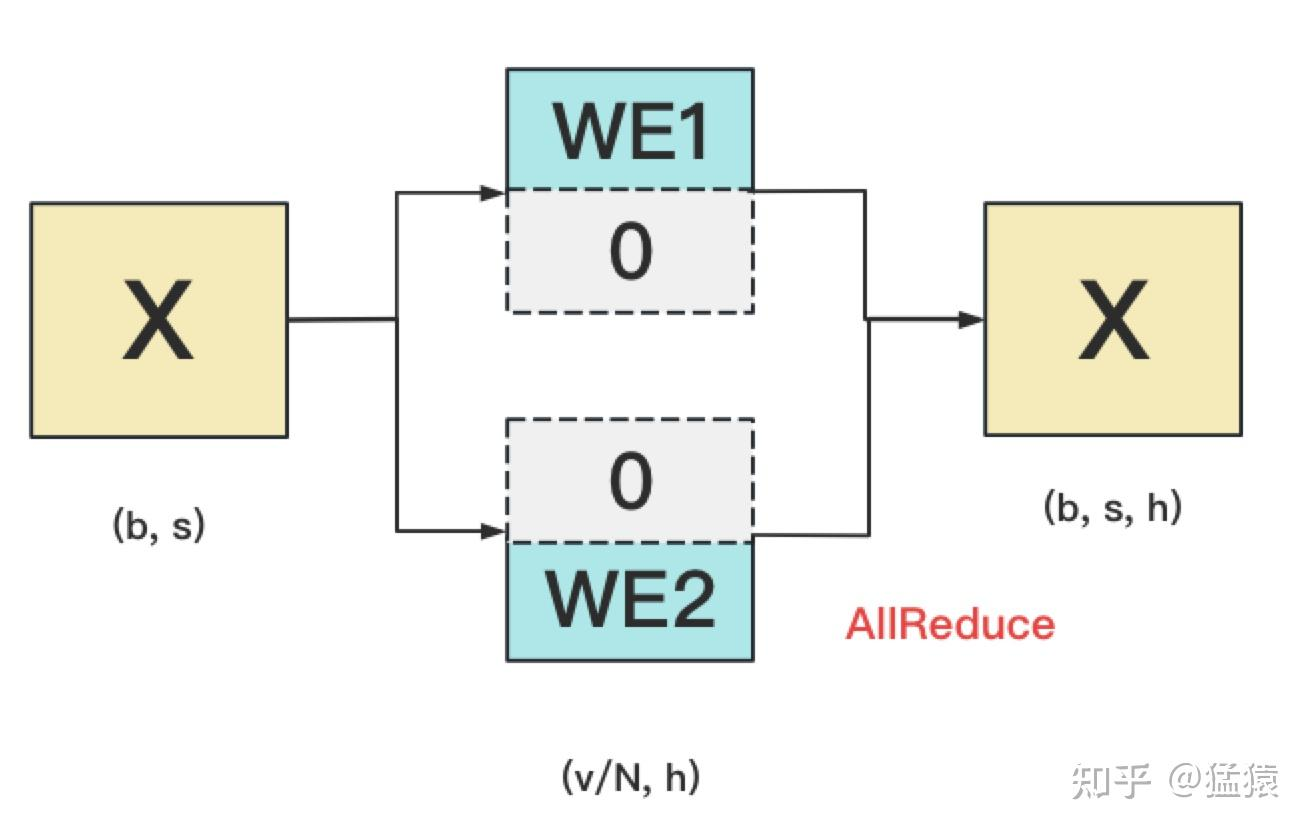
对于输入X，过word embedding的过程，就是等于用token的序号去word embedding中查找对应词向量的过程。例如，输入数据为[0, 212, 7, 9]，数据中的每一个元素代表词序号，我们要做的就是去word embedding中的0，212，7，9行去把相应的词向量找出来。

假设词表中有300个词，现在我们将word embedding拆分到两块GPU上，第一块GPU维护词表[0, 150)，第二块GPU维护词表[150, 299)。当输入X去GPU上查找时，能找到的词，就正常返回词向量，找到不到就把词向量中的全部全素都置0。按此方式查找完毕后，每块GPU上的数据做一次AllReduce，就能得到最终的输入。 例如例子中，第一块GPU的查找结果为[ok, 0, ok, ok]，第二块为[0, ok, 0, 0]，两个向量一相加，变为[ok, ok, ok, ok]

4.2 输出层

输出层中，同样有一个word embedding，把输入再映射回词表里，得到每一个位置的词。一般来说，输入层和输出层共用一个word embeding。其计算过程如下：

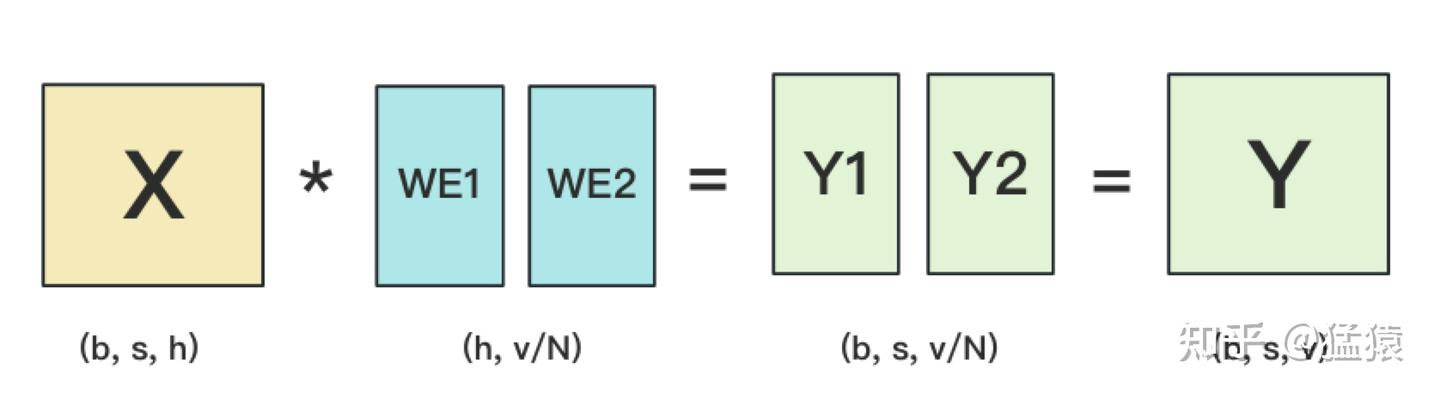
需要注意的是，我们必须时刻保证输入层和输出层共用一套word embedding。而在backward的过程中，我们在输出层时会对word embedding计算一次梯度，在输入层中还会对word embedding计算一次梯度。在用梯度做word embedding权重更新时，我们必须保证用两次梯度的总和进行更新。

当模型的输入层到输入层都在一块GPU上时（即流水线并行深度=1），我们不必担心这点（实践中大部分用Megatron做并行的项目也是这么做的）。

但若模型输入层和输出层在不同的GPU上时，我们就要保证在权重更新前，两块GPU上的word embedding梯度做了一次AllReduce。

5 cross-entroy层

输出层过完embedding：

5.1 原始逻辑 (All Gather) 方案

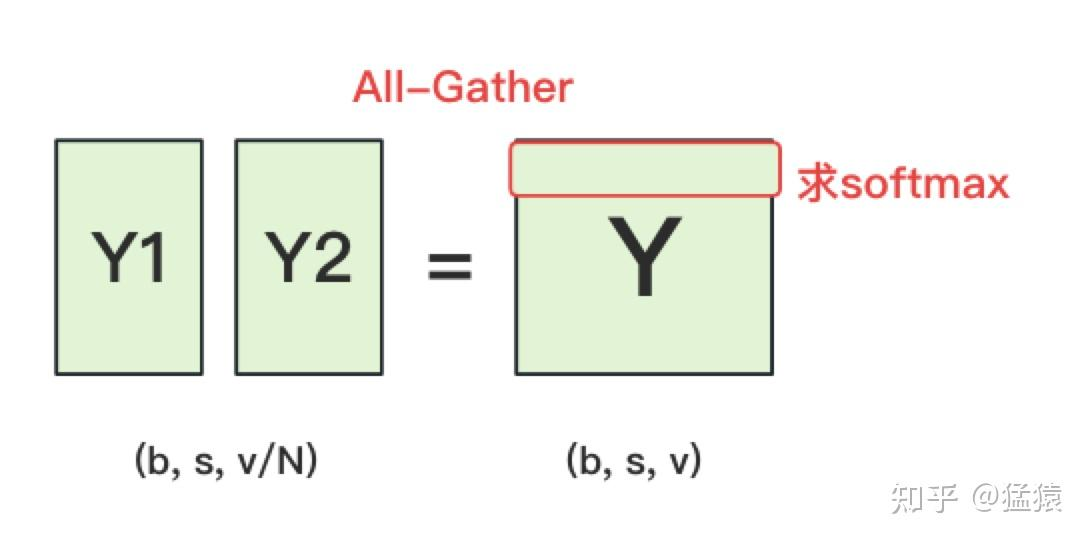
首先，我们看最容易想到的方案。由于词表权重被按列切分到了 $N$ 个 GPU 上，每个 GPU 只能算出自己负责的那一部分词的得分（Partial Logits），其维度为 $(b, s, v/N)$。

• 数据流向：为了计算完整的 Softmax，我们需要拿到所有词的得分。于是，系统调用一次 All-Gather 通信，将各显卡上的局部 Logits 拼接成一个完整的、维度为 $(b, s, v)$ 的全局张量 $Y$。
• 计算逻辑：拼接完成后，每个 GPU 都在本地执行标准的 Softmax 和 Cross Entropy 计算。
• 致命缺陷：显存瓶颈（OOM）。 这种方案虽然逻辑简单，但在大模型面前几乎不可行。假设 Batch Size 为 4，序列长度为 2048，词表大小为 128,000，在使用 FP16 精度时，仅这一个 Logits 张量 $Y$ 就会占用约 2GB 的显存。在并行训练中，每个 GPU 都要存储一份这样的完整张量，会造成极大的显存浪费，甚至直接导致显存溢出。

5.2 优化实现（Parallel Cross Entropy 方案）**

为了解决显存瓶颈，我们引入了更加巧妙的 Parallel Cross Entropy）方案。它的核心哲学是：“如果我只需要全局的统计量，又何必传输整个大张量呢？”

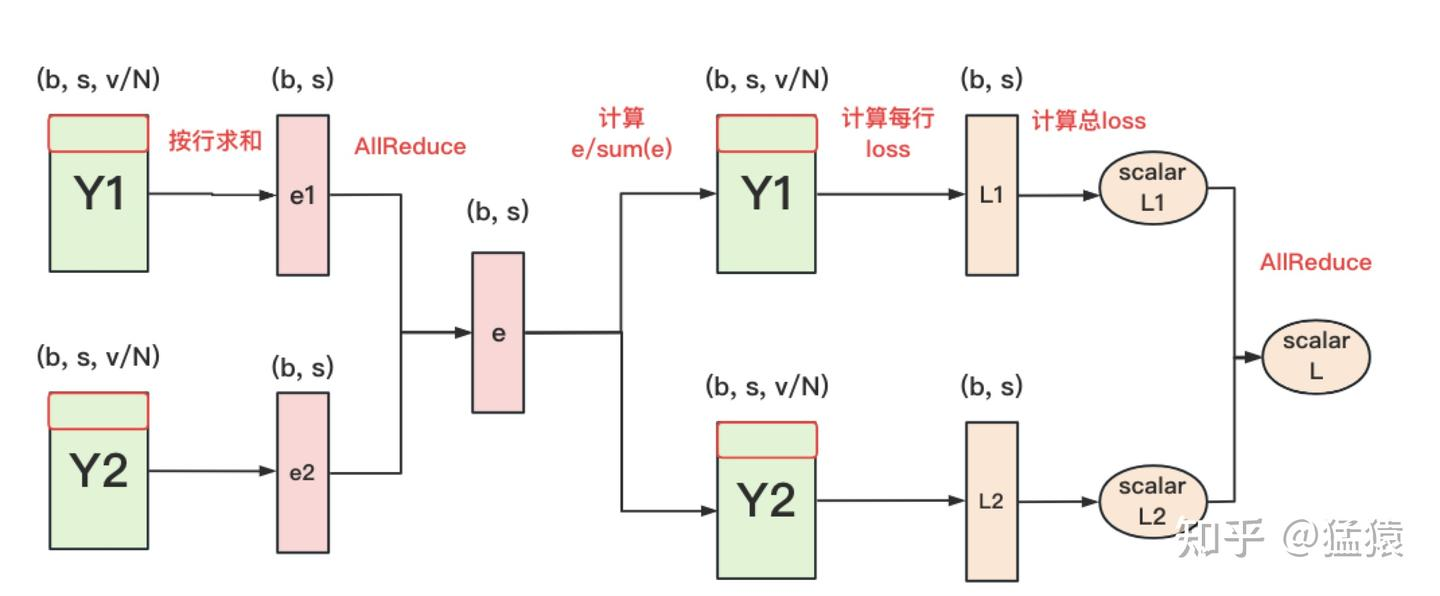
• 衔接逻辑：我们观察到，Softmax 的分母本质上是所有词得分指数值的累加和。既然是求和，我们不需要把所有的词聚齐，可以先在本地算局部和，再同步这个“和”。
• 数据流向三步走：
  1. 局部降维（局部求和）：每个 GPU 计算局部 Logits 的指数和（以及最大值用于数值稳定），得到维度仅为 $(b, s)$ 的小张量 $e_i$。
  2. 极简通信（All-Reduce）：对这些小张量进行一次 All-Reduce。由于维度不含词表大小 $v$，通信量瞬间降低了几个数量级。此时，每个 GPU 虽没有完整的词表得分，却都拥有了计算 Softmax 所需的全局分母。
  3. 分布式损失计算：每个 GPU 结合手中的全局分母和本地的局部得分，计算出属于自己那部分词的 Loss。最后再进行一次标量聚合。

• 每块GPU上，我们可以先按行求和，得到各自GPU上的GPU_sum(e)

• 将每块GPU上结果做AllReduce，得到每行最终的sum(e)，也就softmax中的分母。此时的通讯量为 $b * s$

• 在每块GPU上，即可计算各自维护部分的e/sum(e)，将其与真值做cross-entropy，得到每行的loss，按行加总起来以后得到GPU上scalar Loss。

• 将GPU上的scalar Loss做AllReduce，得到总Loss。此时通讯量为N。

这样，我们把原先的通讯量从 $b * s * v$ 大大降至 $b * s + N$。

对比这两张图，我们可以看到从“图一”到“图二”的质变：

• 显存减负：图二方案彻底抛弃了存储全局大张量 $(b, s, v)$ 的需求，将显存占用从 $O(V)$ 降到了 $O(1)$（相对于词表大小）。
• 通信提速：虽然通信次数多了一次，但通信的数据体量从“整车装运”变成了“传个纸条”，极大地缓解了网络带宽的压力。

这种“先降维、再同步、后局部计算”的技巧，正是 Megatron-LM 等分布式框架能够训练万亿参数模型的底层黑科技之一。

6 总共的通讯开销

在张量模型并行中，我们设每次通讯量为 $\Phi_{TP}$，从上面分析中我们知道每层做4次AllReduce，其通讯总量为 $8\Phi_{TP}$。其中，$\Phi_{TP} = b * s * h$，则通讯总量为 $8 * b * s * h$。

你的描述已经抓住了核心逻辑，但在博客写作中，可以进一步强化“结构对称性”和“通信开销的量化推导”。

以下是为你润色后的版本，包含要点解析和更严谨的开销总结：

6. 张量并行的总通信开销：全局视角

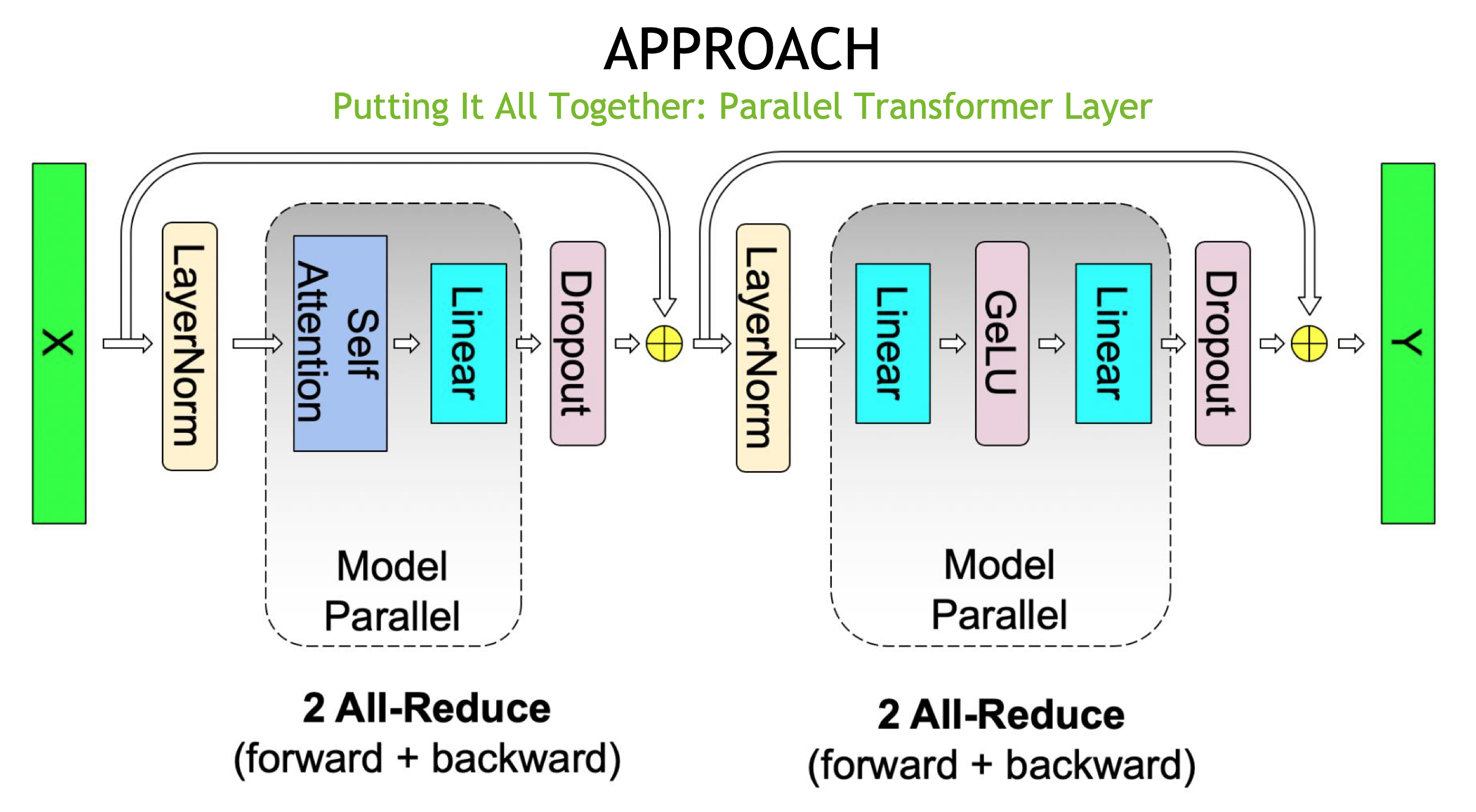
通过前面的分析，我们可以将这些组件“拼装”起来，得到一个完整的 并行 Transformer 层（Parallel Transformer Layer） 实现。如下图所示，Megatron-LM 巧妙地在 Self-Attention 块和 MLP 块中应用了对称的并行逻辑。

6.1 图片要点解析**

1. 两段式结构：一个完整的 Transformer 层由 Self-Attention 和 MLP 两个大的并行块组成。
2. 通信算子的位置：
   • 在每个块的前向传播中，通信发生在 行并行（Row Parallel）线性层之后。由于行并行的输出是各卡分量的“部分和”，必须通过一次 All-Reduce 才能恢复出完整的张量，供给后续的 Add & Norm 使用。
   • 根据前文提到的“共轭关系”，在前向传播中进行 All-Reduce 的位置，其对应的反向传播输入端也必然需要一次 All-Reduce 来同步梯度。
3. 计算与通信的解耦：LayerNorm 和 Dropout 依然是在每个 GPU 上对同步后的完整数据进行本地计算。

6.2 TP 通信开销定量分析

为了量化开销，我们设单次通信张量的大小为 $\Phi_{TP}$。在标准 Transformer 结构中，隐藏层维度为 $h$，序列长度为 $s$，批大小为 $b$，则： \(\Phi_{TP} = b \times s \times h\)

根据图片展示的逻辑，我们可以推导出单层 Transformer 在一次完整的训练迭代（前向+后向）中的总通信开销：

• Self-Attention 块：前向 1 次 All-Reduce，后向 1 次 All-Reduce，共计 2 次。
• MLP 块：前向 1 次 All-Reduce，后向 1 次 All-Reduce，共计 2 次。
• 单层总计：每层 Transformer 总共执行 4 次 All-Reduce。

6.4 关于通讯总量的计算：

在分布式计算中，一次 All-Reduce 操作的通信量通常按其传输的数据大小来衡量。若以单次 All-Reduce 涉及的数据量 $b \times s \times h$ 为基准：

• 算子调用次数：4 次（前向 2 次 + 后向 2 次）。
• 通信数据总量： 考虑到 All-Reduce 在标准环形（Ring）算法下的通信量约为 $2 \times \frac{N-1}{N} \times \Phi_{TP}$，在 $N$ 很大时近似为 $2\Phi_{TP}$。因此，单层训练的总通信数据量可量化为： \(Total\_Comm = 4 \times (2 \times b \times s \times h) = 8 \times b \times s \times h\)

总结： 张量并行的通信频率非常高（每层 4 次同步），且通信量与隐藏层大小 $h$ 成正比。这意味着 TP 对 GPU 节点间的互联带宽（如 NVLink）有着极高的要求，这正是 TP 通常只在机内（Intra-node）使用的原因。