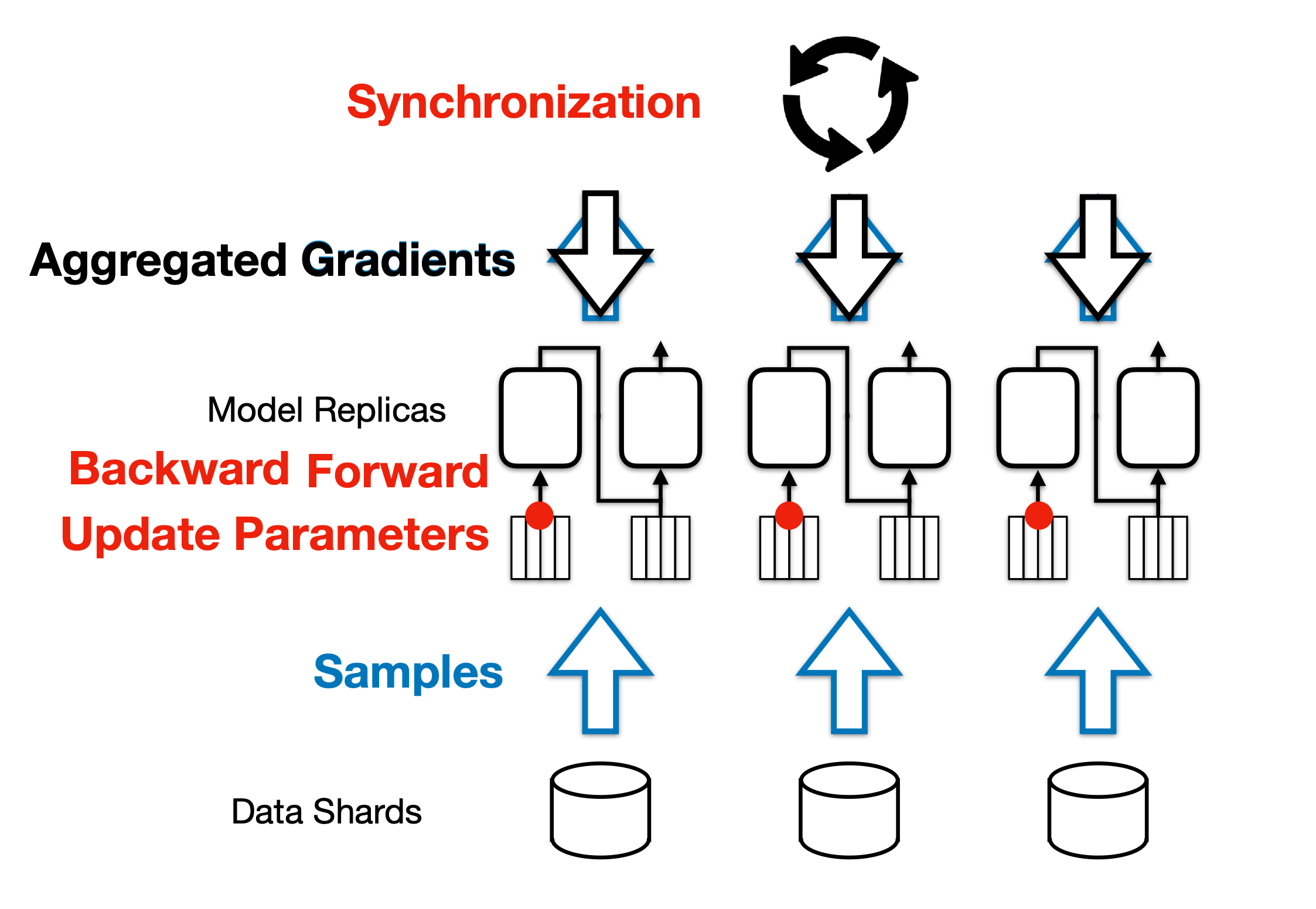
1 Transformer 训练的4个阶段
如图所示,transformer 训练有4个阶段
- 前向传播
- 反向传播
- 梯度聚合(AllReudce Aggregation)
- 参数更新(Optimizer Step)
2 算子融合(Kernel Fusion)策略
2.1 概念
-
朴素实现:
C = A + B E = C + D需要 4 次 load、2 次 store、2 次矩阵加,并且 需要两次 kernel 启动(launch)。
-
融合后(自定义单个 kernel):
E = A + B + C只需 3 次 load、1 次 store、2 次矩阵加,一次 kernel 启动。
Benefits(收益) • 减少 kernel 启动开销(kernel launch overhead) • 减少中间张量的显存读写(extra memory access)
MHA 与 FFN 等结构中,非 GEMM 的大量逐元素/简单变换算子适合融合以降低 IO 和 launch 开销。
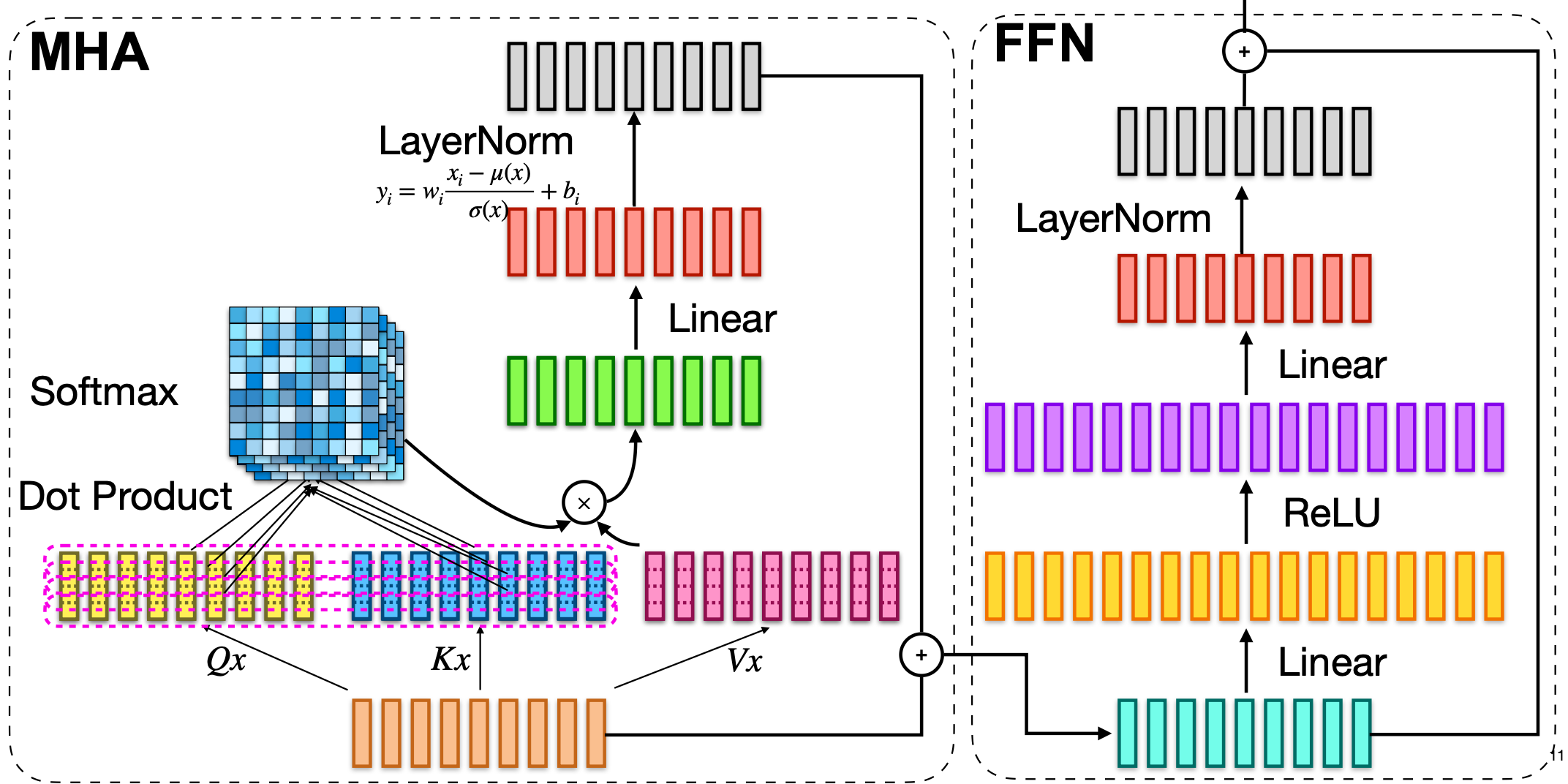
针对于非GEMM(图中蓝色element wise与粉色 reduce)的操作,通过融合进行加速,

2.2 Embedding 前向融合
embedding + dropout的 融合优化
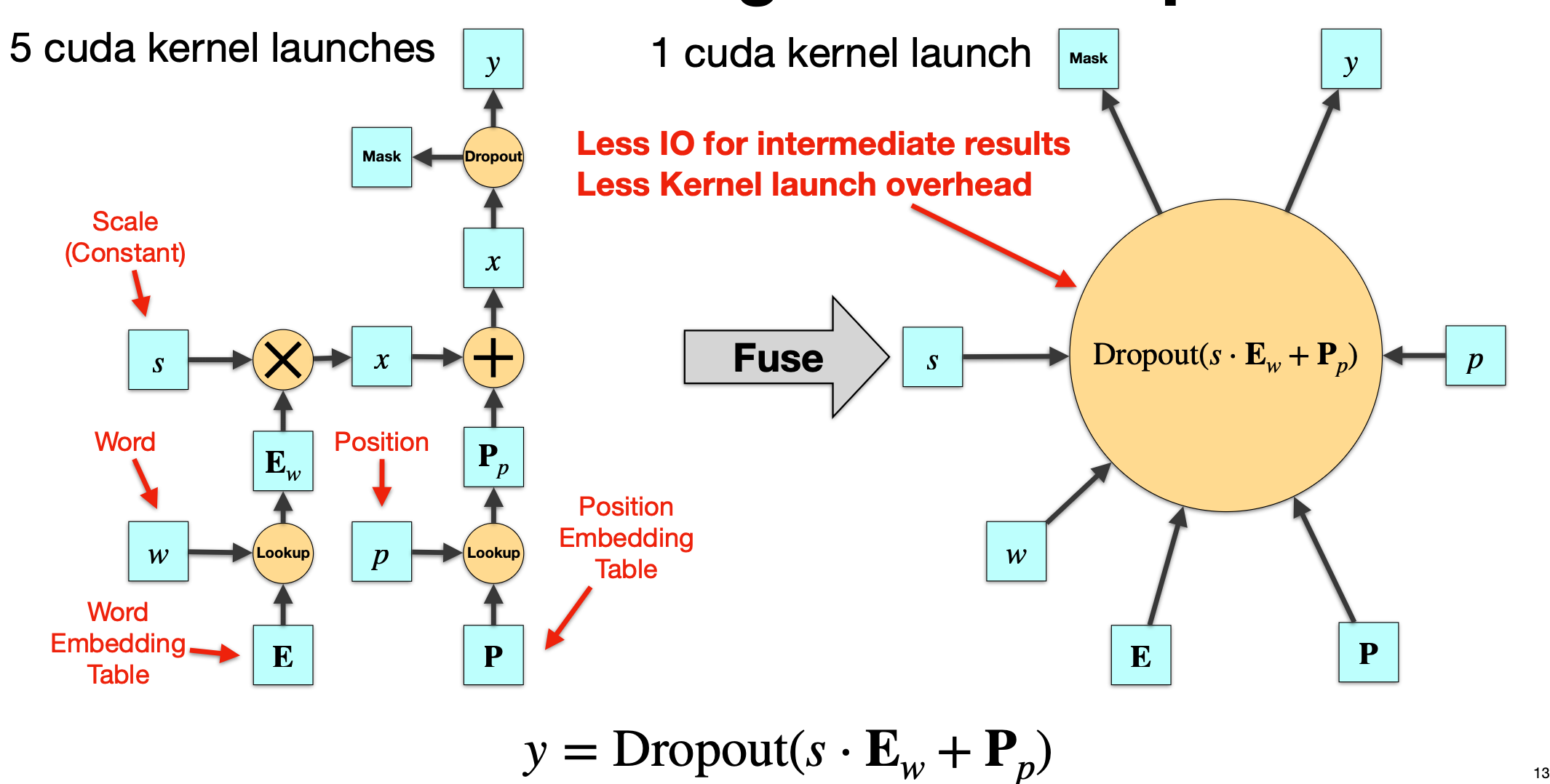
未融合(左图):需依次执行并写回中间结果
- Word Lookup:从词表 E 中取出 w 对应的 embedding,得到 E_w
- Scale(通常为 $\sqrt{d_\text{model}}$)
- Position Lookup:从位置表 P 中取出对应的位置 embedding,得到 P_p
- Add:将词向量和位置向量相加
- Dropout:对相加后的结果做随机丢弃 对应 5 次 kernel 启动 与多次全局内存读写。
融合后(右图):在单个 kernel 内
- 同时完成词表/位置表 lookup
- 在寄存器/共享内存中完成 scale + add
- 直接做 dropout 并写回最终结果 → 一次 kernel,显著降低 IO 与 launch。
2.3 Embedding 反向融合
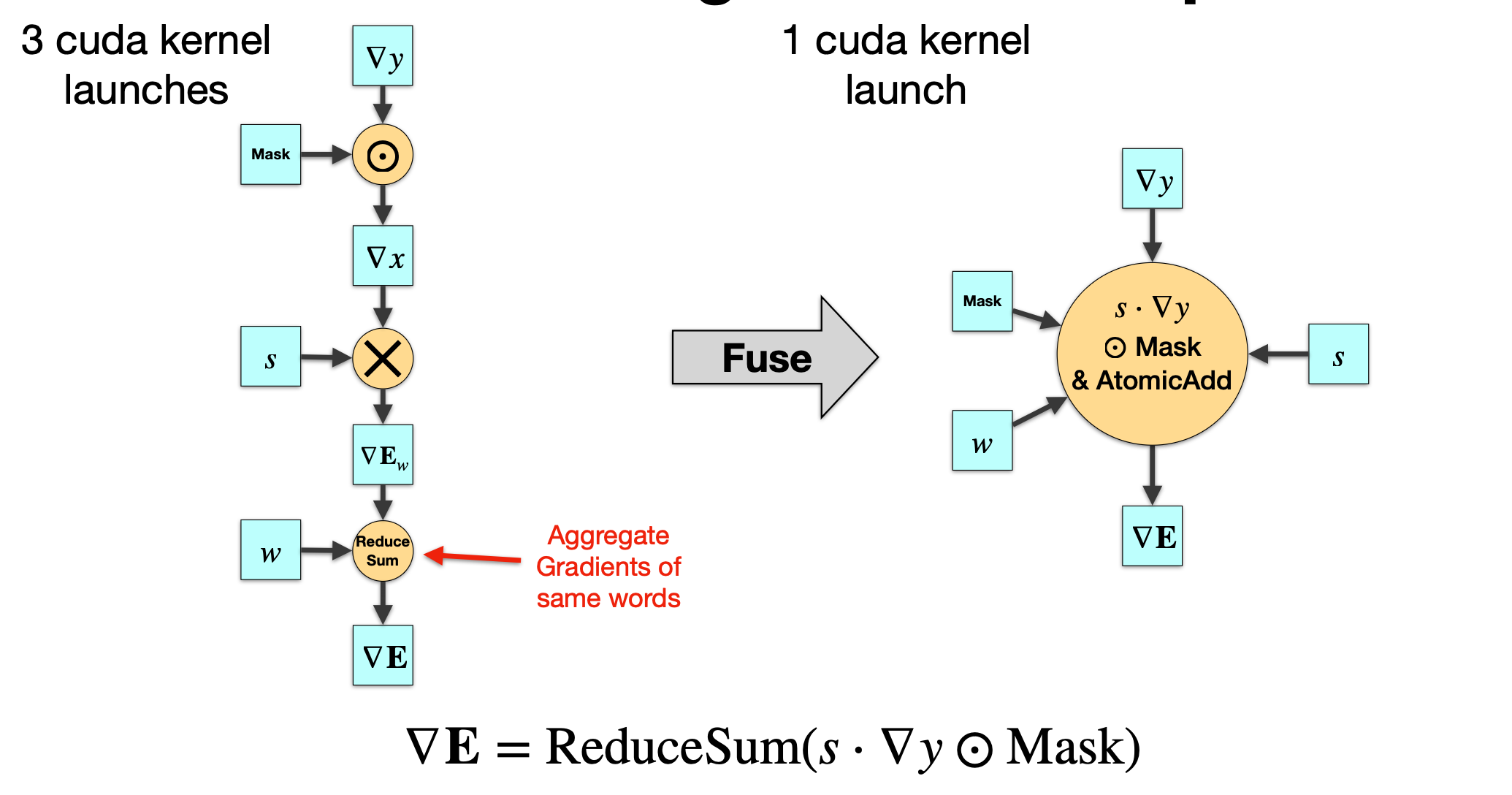
2.3.1 未融合(左)——3 个 kernel
- Mask 乘法:
- $\nabla x=\nabla y \odot \text{Mask}$
- 为了配合前向的 Dropout(或 Padding Mask),在对应位置把梯度清零
- Scale:
- $\nabla E_w=s\cdot\nabla x$,
- 将梯度按 embedding 的缩放系数缩
- ReduceSum 聚合:
- 因为在一个 batch 内,多个 token 可能指向同一个词(同一个索引)
- 所以需要将这些梯度加到词表参数矩阵
E的对应行上 - $\nabla E = \text{ReduceSum}_{\text{tokens}}( \nabla E_w )$
- 如果
w = [2, 3, 2],就要把 token1 和 token3 的梯度加到词表的第 2 行上。 - 这一步需要做 scatter+reduce
2.3.2 融合(右)——1 个 kernel
右图将上述三步融合成一个自定义 CUDA kernel,一次完成所有操作:
\[\nabla E = \text{ReduceSum}( s \cdot \nabla y \odot \text{Mask} )\]特点:
- 在同一个 kernel 内完成 mask 乘法、scale、以及 scatter+reduce 操作
- 使用
AtomicAdd将多个 token 对应的梯度安全地累加到 embedding 表的同一行上(并行安全) -
避免了:
- 多次 kernel 启动
- 中间梯度张量的写回 / 读出
- 多次访存 参考代码(ByteDance LightSeq)
- 前向
lookup_scale_pos_dropout(节选)
lookup_scale_pos_dropout 里: Word Embedding Lookup
Positional Embedding Lookup
float4 *output4 = reinterpret_cast<float4 *>(output);
const float4 *embeddings4 = reinterpret_cast<const float4 *>(embeddings);
const float4 *pos_embeddings4 =
reinterpret_cast<const float4 *>(pos_embeddings);
dropout mask
for (uint i = start; i < end; i += blockDim.y) {
curand_init(seed, i, 0, &state);
float4 rand4 = curand_uniform4(&state);
uint8_t m[4];
// dropout mask
m[0] = (uint8_t)(rand4.x > dropout_ratio);
m[1] = (uint8_t)(rand4.y > dropout_ratio);
m[2] = (uint8_t)(rand4.z > dropout_ratio);
m[3] = (uint8_t)(rand4.w > dropout_ratio);
int offset = i - target_pos * embedding_dim;
// step is non-zero only in inference
float4 e4 = embeddings4[tid * embedding_dim + offset];
float4 pe4 =
pos_embeddings4[(token_pos_id + step) * embedding_dim + offset];
float4 res4;
// apply dropout
float scale_mask[4];
scale_mask[0] = dropout_scale * m[0];
scale_mask[1] = dropout_scale * m[1];
scale_mask[2] = dropout_scale * m[2];
scale_mask[3] = dropout_scale * m[3];
uint8_t clip_mask[4];
if (clip_max) {
e4.x = fake_quantize(e4.x, clip_max_val, clip_mask[0], 2);
e4.y = fake_quantize(e4.y, clip_max_val, clip_mask[1], 2);
e4.z = fake_quantize(e4.z, clip_max_val, clip_mask[2], 2);
e4.w = fake_quantize(e4.w, clip_max_val, clip_mask[3], 2);
}
//scale
res4.x = (emb_scale * e4.x + pe4.x) * scale_mask[0];
res4.y = (emb_scale * e4.y + pe4.y) * scale_mask[1];
res4.z = (emb_scale * e4.z + pe4.z) * scale_mask[2];
res4.w = (emb_scale * e4.w + pe4.w) * scale_mask[3];
output4[i] = res4;
uint32_t *m4 = reinterpret_cast<uint32_t *>(m);
if (clip_max) {
m4[0] = m4[0] | reinterpret_cast<uint32_t *>(clip_mask)[0];
}
dropout_mask4[i] = m4[0];
}
- 反向
d_lookup_scale_pos_dropout(节选)
for (uint i = start; i < end; i += blockDim.y) {
// dropout scale
float4 go4 = grad_output4[i];
uint32_t m4 = dropout_mask4[i];
uint8_t *m4_ptr = reinterpret_cast<uint8_t *>(&m4);
float4 res4;
res4.x = emb_scale * go4.x * (m4_ptr[0] & 1) * scale;
res4.y = emb_scale * go4.y * (m4_ptr[1] & 1) * scale;
res4.z = emb_scale * go4.z * (m4_ptr[2] & 1) * scale;
res4.w = emb_scale * go4.w * (m4_ptr[3] & 1) * scale;
int offset = i - target_pos * embedding_dim;
int idx = (tid * (embedding_dim) + offset) << 2;
clip_bwd(res4.x, temp_cmax_grad, res4.x, m4_ptr[0], 2);
thread_cmax_grad += temp_cmax_grad;
clip_bwd(res4.y, temp_cmax_grad, res4.y, m4_ptr[1], 2);
thread_cmax_grad += temp_cmax_grad;
clip_bwd(res4.z, temp_cmax_grad, res4.z, m4_ptr[2], 2);
thread_cmax_grad += temp_cmax_grad;
clip_bwd(res4.w, temp_cmax_grad, res4.w, m4_ptr[3], 2);
// reduction sum
thread_cmax_grad += temp_cmax_grad;
atomicAdd(grad_embeddings + idx, res4.x);
atomicAdd(grad_embeddings + idx + 1, res4.y);
atomicAdd(grad_embeddings + idx + 2, res4.z);
atomicAdd(grad_embeddings + idx + 3, res4.w);
}
// Gradient clipping Gradient accumulation
if (grad_clip_max) {
__shared__ float block_cmax_grad;
if (threadIdx.x == 0 && threadIdx.y == 0) {
block_cmax_grad = 0;
}
__syncthreads();
if (thread_cmax_grad != 0) {
atomicAdd(&block_cmax_grad, thread_cmax_grad);
}
__syncthreads();
if (threadIdx.x == 0 && threadIdx.y == 0) {
if (block_cmax_grad != 0) {
atomicAdd(&grad_clip_max[0], block_cmax_grad);
}
}
}
完整见: LightSeq
2.4 Fused Softmax + CrossEntropy + Gradient(前后向融合)
2.4.1 损失函数定义
\[[ \mathcal{L} = - \sum_i p_i \log q_i ]\]- $q = \text{Softmax}(h)$:模型输出经过 softmax 后的概率分布
- $ p $:“ground truth” 的目标分布,但不是严格 one-hot,而是经过 label smoothing 处理
- $ h $:模型的 logits(未经过 softmax)
2.4.2 Label Smoothing 公式
\[p = (1 - \alpha) y + \frac{\alpha}{V} \cdot 1\]- $y$:原始的 one-hot 向量
- $ \alpha $:smoothing 参数,0<α<1
-
$ V $:词表大小
- ground truth 的位置概率是 $ 1 - \alpha + \frac{\alpha}{V} $
- 其他所有 token 的概率都是 $ \frac{\alpha}{V} $
目的: 避免模型过度自信、提升泛化能力,是 Transformer 论文中的标准 trick。
2.4.3 Softmax 的输出与梯度
输出: \([ q_i = \frac{e^{h_i}}{\sum_j e^{h_j}} ]\) 梯度: \(\frac{\partial q_i}{\partial h_j} = \begin{cases} -q_i q_j, & i \neq j \ q_i (1 - q_i), & i = j \end{cases}\)
这是经典 softmax 导数形式,之后会用在链式法则中。
2.4.4 对 logits 的梯度推导
我们要求: \(\nabla_{h_i} \mathcal{L} = \frac{\partial \mathcal{L}}{\partial h_i}\) 分两种情况分析:
(a) 当 i 是 ground truth 的 index = k
\(\nabla_{h_k} \mathcal{L} = q_k - \frac{\alpha}{V} - 1 + \alpha\)
(b) 当 i ≠ k
\[\nabla_{h_i} \mathcal{L} = q_i - \frac{\alpha}{V}\]这里用到了 label smoothing 后的目标分布 ( p ),因此梯度不再是简单的 ( q - y ),而是:
- ground truth 位置:$ q_k - (1-\alpha + \frac{\alpha}{V}) $
- 非 ground truth 位置: $ q_i - \frac{\alpha}{V} $
2.4.4 关键梯度
\[\boxed{\nabla_h \mathcal{L}=q-p}\]也就是说:
- 对 logits 的梯度,就是 softmax 输出 $ q $ 减去(经过 label smoothing 的)目标分布 ( p )。
- 这个公式在实现中非常高效:softmax + cross entropy 反向传播几乎不需要额外 kernel,框架会直接用这个差值作为梯度。
实现上可直接用 $q-p$ 作为 logits 的梯度,避免显式回传 softmax/log/CE 的细节,从而实现前后向的 fused kernel。
这也是像 Megatron-LM / DeepSpeed / PyTorch 都使用 Fused Softmax + CrossEntropy + Gradient 的原因,避免分别计算 softmax、log、loss、再反向。
2.4.5 补充说明:为什么要把这个单独作为“Criterion Operator Gradient”
因为在实际的 Transformer 训练里:
- 最后的
logits → softmax → cross_entropy是整个计算图的末端 - 其梯度是整个模型反向传播的起点
- 直接用
g = q - p是高效实现的基础(不需要手动反向传播 softmax)
在实现上,PyTorch 的 nn.CrossEntropyLoss + F.log_softmax 已经内置了这种 fused backward
2.5 Fused Criterion Operator(损失算子融合)
Transformer 训练最后一层(Softmax + Cross Entropy Loss)的 算子融合(Operator Fusion
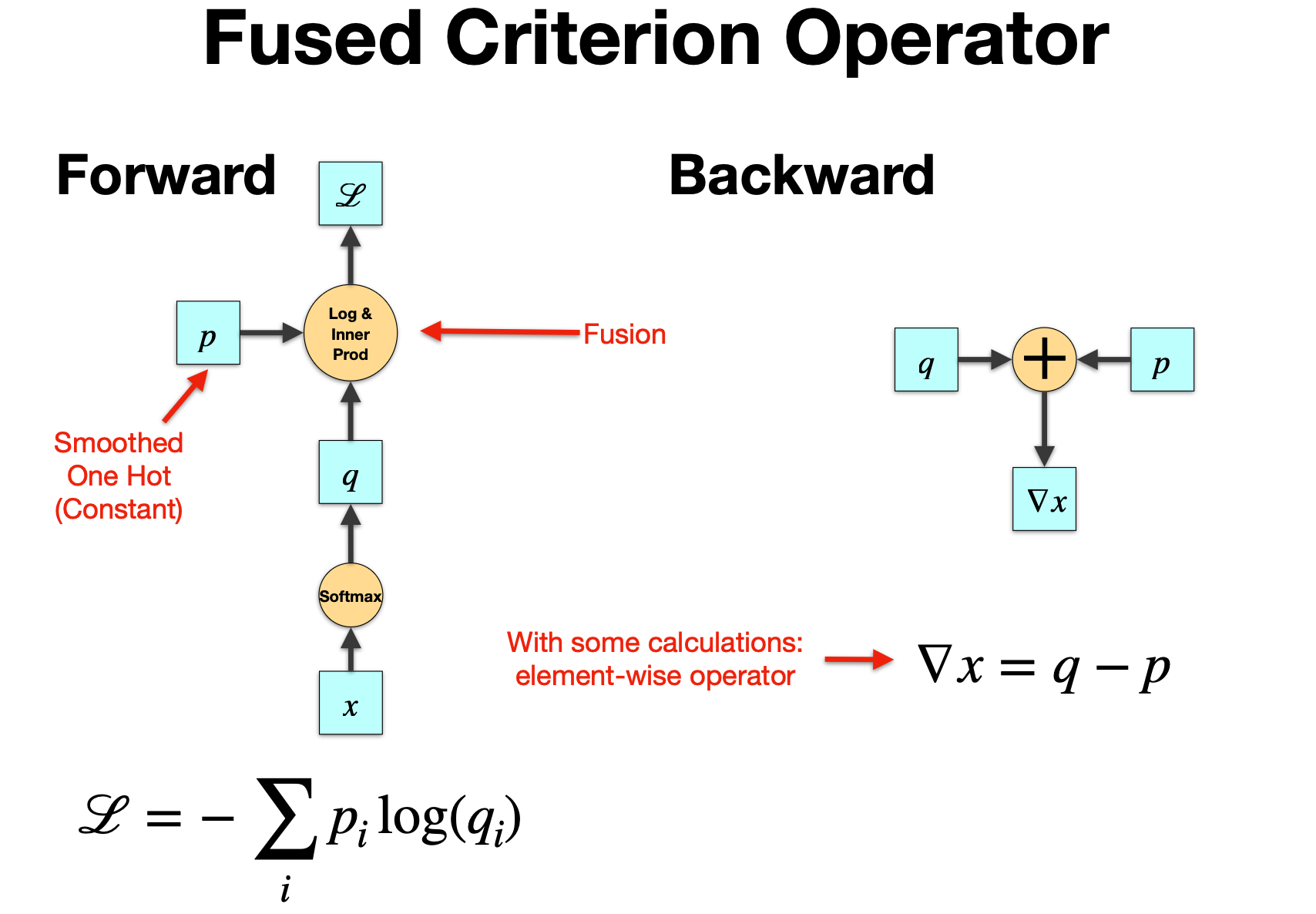
2.5.1 未融合的计算流程
通常情况下,计算交叉熵损失的流程如下:
-
Softmax: \(q = \mathrm{Softmax}(x)\) 把 logits ( x ) 转为概率分布 ( q )。
-
取 log: 对 softmax 输出 ( q ) 取对数,得到 ( \log q )。
-
与目标分布 p 相乘,再求和(内积): \(\mathcal{L} = - \sum_i p_i \log q_i\) 这是 Cross Entropy 损失(这里的 p 是 smoothed one-hot label)。
以上三步在 GPU 上如果逐个实现,会对应 三个 kernel 启动:
- softmax kernel
- log kernel
- elementwise mul + reduce kernel
而且每一步之间都需要把中间张量写回显存、再从显存中读出来,产生大量 global memory IO。
2.5.2 Forward 融合
图中左边 Forward 的部分,用一个黄色的 “Log & Inner Prod” 算子表示: 将:
SoftmaxLogp * log(q)并求和(即 loss)
融合到一个单一 CUDA kernel 内完成,这就是所谓的:
Fused Softmax + Cross Entropy Forward
这样做的好处:
- 只需要 一次 kernel launch
q不需要写回内存后再取 loglog q不需要单独存储p * log q可以边算边 accumulate
在实现上,这个 fused kernel 会一边计算 softmax(可能用 online normalization trick),一边在寄存器里对 p_i * log(q_i) 累加,从而得到最终 loss。
2.5.3 Backward 融合(右图)
右图是反向传播。核心公式在前面推导过:
\[\nabla_x = q - p\]也就是说,如果我们要对 logits ( x ) 求梯度:
- 不需要显式反向传播 softmax、log、cross entropy 的每一部分
- 只要直接计算
q - p即可(element-wise)
因此,Backward 部分也可以融合成 一个简单的 element-wise kernel:
- 读取 softmax 输出 q(可能 forward 时保留)
- 读取 p(ground truth)
- 直接
q - p写入梯度张量 ∇x
而如果不融合,理论上需要:
- softmax backward kernel(计算 softmax 的雅可比矩阵乘积)
- cross entropy backward kernel(再乘 p / q)
- 加起来 kernel 调用多 + 中间张量多
2.5.4 融合性能对比
| 操作阶段 | 未融合 | 融合后 |
|---|---|---|
| Forward | softmax → log → elementwise mul → reduce(多个 kernel) | 1 次 kernel 内完成所有 |
| Backward | softmax backward + CE backward | 直接用 q - p 一步完成 |
| IO | 多次 global memory 读写 | 大量计算在寄存器 / shared mem 完成 |
| Launch Overhead | 多次 kernel 启动 | 1~2 次 kernel 启动(前向+反向) |
在大模型训练中,这一步在每个 token、每个 batch、每个 GPU 都会调用一次,因此融合能明显减少:
- launch overhead
- memory IO
- 中间 tensor allocation
Megatron-LM/DeepSpeed/PyTorch AMP 等均采用类似策略。
2.6 Layer-Batched Cross Attention(按层打包的 Cross-Attn)
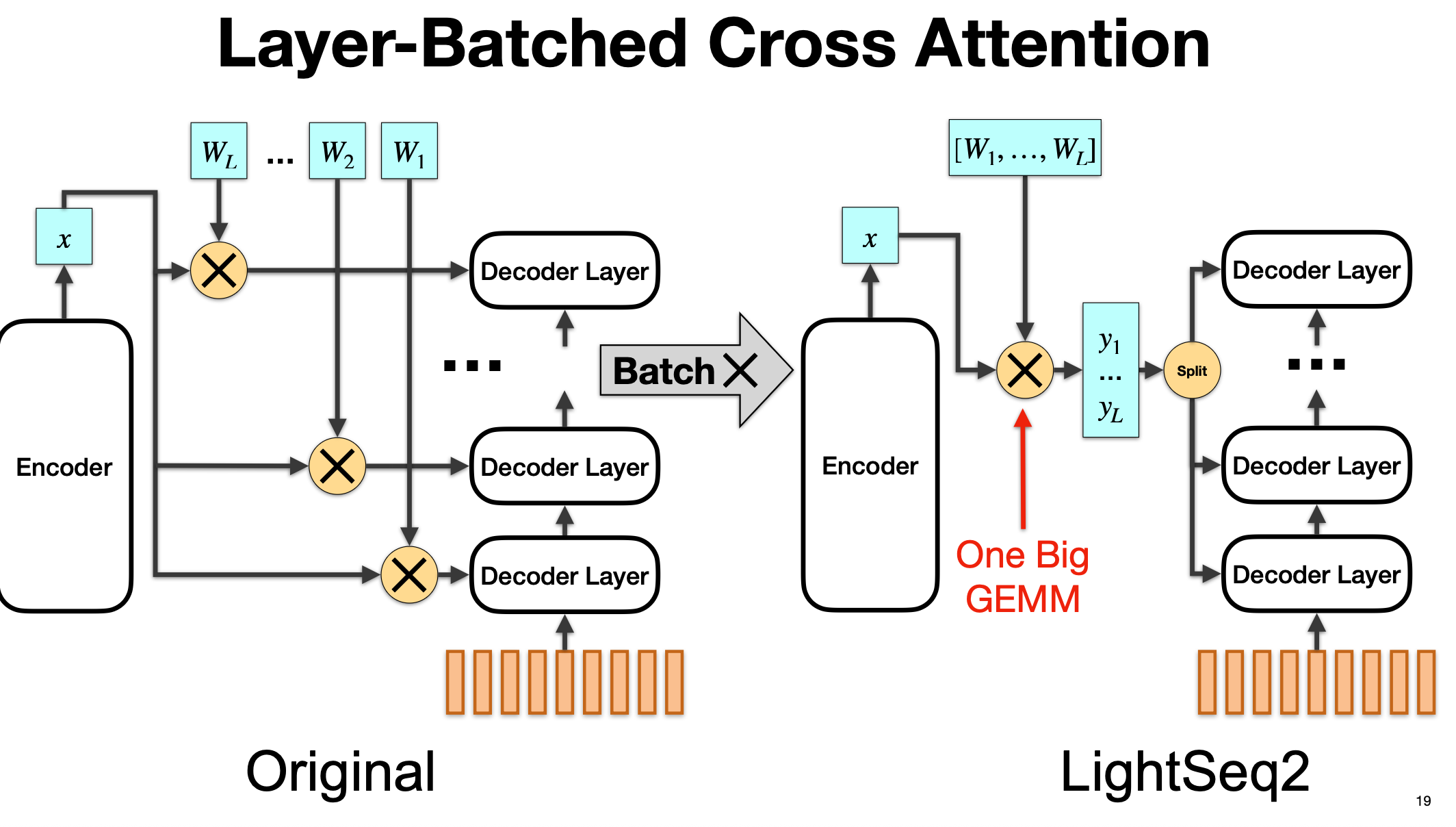
核心目标是:在 Transformer 解码器的多层结构中,将多个小矩阵乘法(GEMM)合并成一个大矩阵乘法,以充分利用 GPU 的吞吐能力,减少 kernel 启动和调度开销。
2.6.1 原始实现(左图)
左图描述的是标准 Transformer 中 Decoder 的 Cross Attention 结构:
- Encoder 输出
x(shape 可能是 [batch, seq_len_enc, d_model])。 - Decoder 有 L 层,每一层都有自己的 Cross Attention 权重矩阵 ( W_1, W_2, \ldots, W_L )。
- 在每一层中,都会单独对
x做一次矩阵乘法: \(y_l = x W_l\) 并将结果传入对应的 decoder layer 的 cross-attention 子层。 -
因为有 L 层,所以需要执行 L 次单独的 GEMM(矩阵乘法),每次维度相对较小(d_model × d_k),导致:
- 需要 L 次 kernel 启动
- GPU 计算吞吐率不高(小 GEMM 性能较差)
- 重复读取同一个 encoder 输出 x,增加内存带宽压力
这种实现方式虽然直观,但效率不高,特别是在 L 比较大时(例如 decoder 有几十层)。
2.6.2 Layer-Batched 优化(右图)
LightSeq2 提出的优化方案,思想是:
-
将所有 decoder 层的 cross-attention 权重矩阵 ( $W_1$, $\ldots$, $W_L$ ) 拼接在一起,形成一个大的 block 矩阵: \(W_{\text{big}} = [W_1, W_2, \ldots, W_L]\) 例如,如果每个 W 的形状是 [d_model, d_k],拼接后就是 [d_model, L×d_k]。
-
对 encoder 输出
x只进行 一次大的矩阵乘法: \(Y_{\text{big}} = x \times W_{\text{big}}\) 这是一个大规模 GEMM,GPU 上执行效率更高(大 GEMM 可以更充分利用 Tensor Cores 和 CUDA 并行度)。 -
得到
Y_big之后,再把它按照 L 个 decoder 层的维度切分(Split),分配给各个 decoder 层对应的 cross-attention 子层使用。
2.6.3 优化的关键点
- 原本是 L 次小 GEMM → 优化为 1 次大 GEMM
- 避免了重复加载 encoder 输出 x
- 大幅减少 kernel 启动次数(L 次 → 1 次)
- 大矩阵乘法的效率更高(更高的 arithmetic intensity,更接近 cuBLAS 高效区间)
- 这就是图中标出的 “One Big GEMM”
这对于 decoder 有大量层(例如 24 层以上)时,性能提升非常明显。
3 减少同步操作
3.1 LayerNorm Forward(重写统计量,合并一次归约)
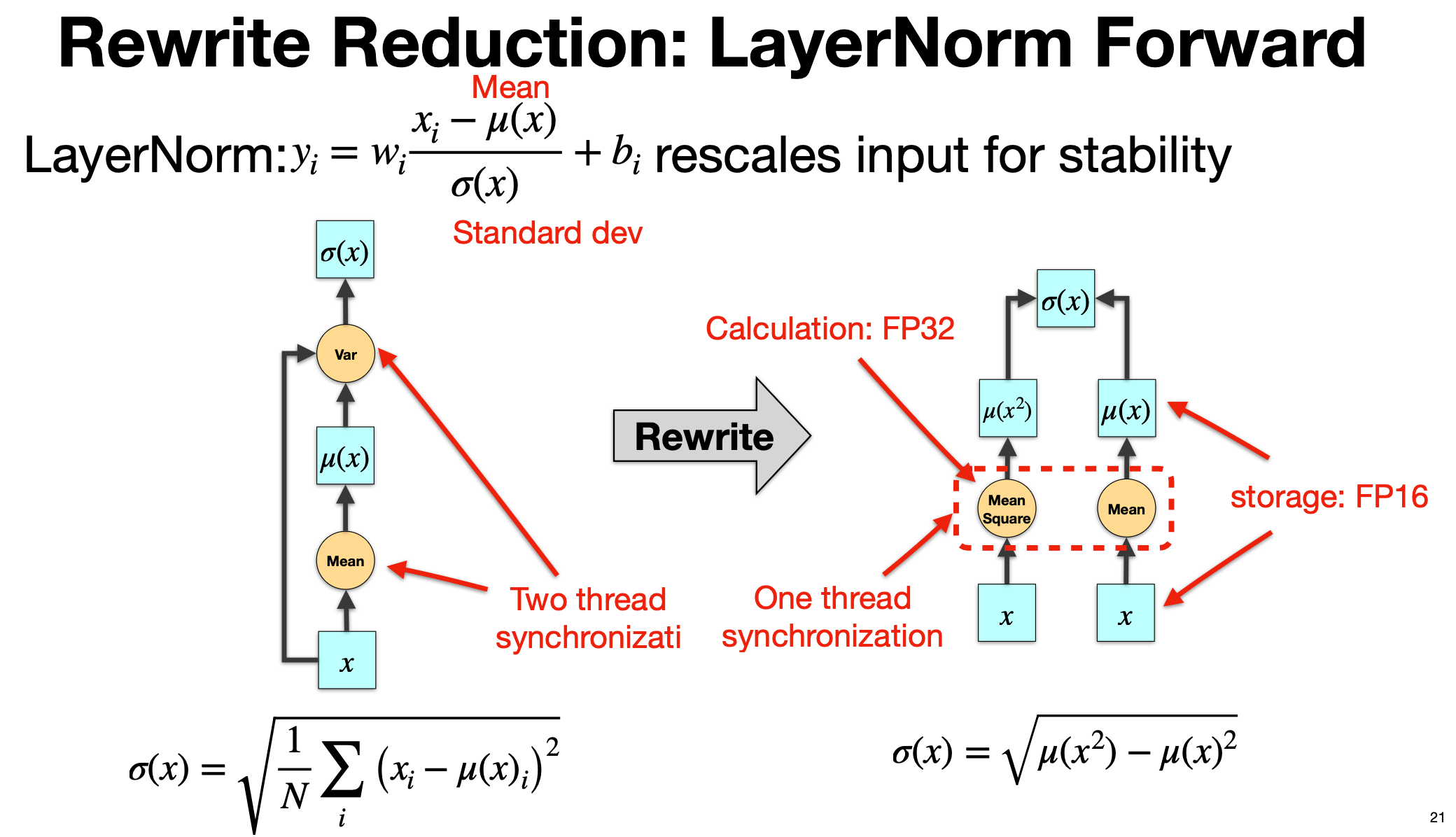
减少 GPU 上的 线程同步开销
3.1.1 左侧:原始的 LayerNorm Forward 计算
LayerNorm 的基本公式是:
\(y_i = w_i \frac{x_i - \mu(x)}{\sigma(x)} + b_i\) 其中:
- $(\mu(x))$:均值
- $\sigma(x)$:标准差
- $w_i, b_i$:可训练的缩放和平移参数
标准差的计算为: \(\sigma(x) = \sqrt{\frac{1}{N}\sum_{i}(x_i - \mu(x))^2}\) 在标准实现中:
-
第一步:计算均值 μ(x)
- 对输入
x做一次 reduction(求和 → 除以 N) - 需要一次线程块内的同步(例如 CUDA 的
__syncthreads())
- 对输入
-
第二步:计算方差 Var(x)
- 再次对
(x - μ)^2做一次 reduction - 再需要一次同步
- 再次对
-
第三步:取平方根得到 σ(x)
这意味着:
- 同一个 tensor
x要被读取两次 - 要做两次全局 reduction
- 在 GPU kernel 中需要 两次线程同步(Two thread synchronization),如图左红色箭头所示
在大模型中,LayerNorm 很频繁(几乎每层 transformer block 都有),而它本身算量不大,容易变成 同步瓶颈
3.1.2 右侧:Rewrite 后的优化计算
数学重写: \(\sigma(x) = \sqrt{\mu(x^2) - \mu(x)^2}\) 即:
- 先求 均值 μ(x)
- 再求 均方值 μ(x²)
- $σ(x)$ 可以通过两者的关系直接算出来,而不必先算均值再回去遍历 $(x - μ)²$
因此:
- 同时对
x做两类统计:- Mean(x)
- Mean(x²)
- 这两个统计都可以在 一次遍历 x 的过程中 完成,并且可以放在同一个 kernel 内
- 只需要 一次 reduction(一次线程同步) 就能同时得到 μ(x) 和 μ(x²)
- 最终用公式 $σ² = μ(x²) - μ(x)²$ 算出标准差
3.1.3 优化对比
| 项目 | 原始方式 | 重写后 |
|---|---|---|
| 计算步骤 | 先算 μ,再算 (x-μ)² 再算均值 | 一次计算 μ(x) 与 μ(x²) |
| Reduction 次数 | 2 次 | 1 次 |
| 线程同步 | 2 次 | 1 次 |
| 访存 | 2 遍读 x | 1 遍读 x |
| 数值精度 | 方差计算中保持 FP32 | 相同(右图注明 Calculation: FP32, Storage: FP16) |
这类优化对 LayerNorm 这类 小算子(low arithmetic intensity) 来说非常重要。它们通常不是计算瓶颈,而是 同步、访存和 kernel 启动开销的瓶颈。减少一次同步和一次访存可以显著降低延迟
3.2 LayerNorm 反向优化
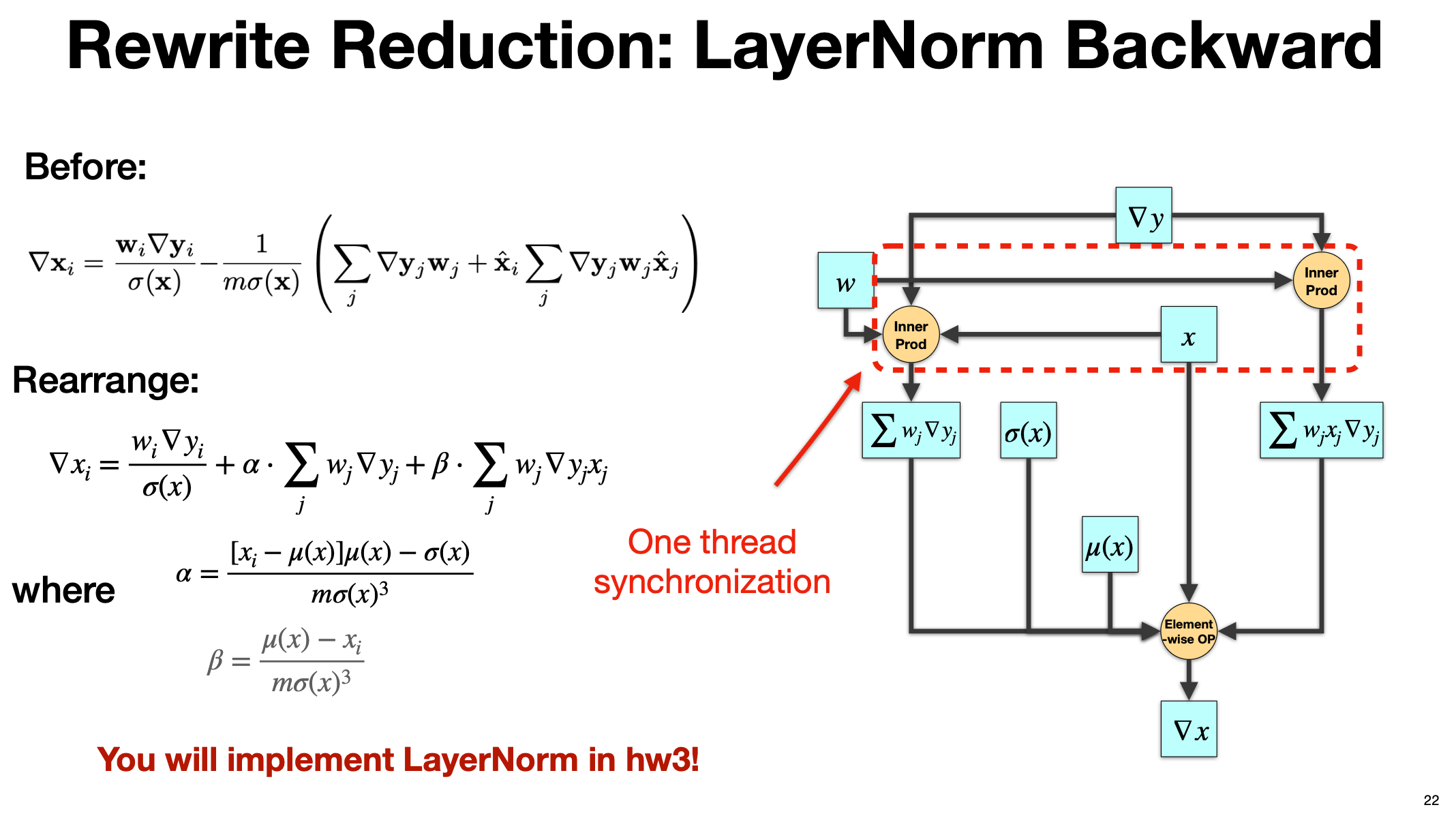
公式重写把原本需要多次全局归约(reduction)的项,改写为只需要一次线程同步即可完成的实现方式,从而降低同步/访存开销
3.2.1 优化前
给出的是对输入分量 (x_i) 的梯度: $$
\nabla x_i = \frac{w_i \nabla y_i}{\sigma(x)} -\frac{1}{m ,\sigma(x)}\left( \sum_j \nabla y_j w_j ;+; \hat{x}_i \sum_j \nabla y_j w_j \hat{x}_j \right) $$ 其中 $m$ 为归一化维度长度,$\hat{x}_i=(x_i-\mu)/\sigma$ 可见需要两类全局求和(对 $j$ 的 reduce):
- $\sum_j \nabla y_j w_j$
- $\sum_j \nabla y_j w_j \hat{x}_j$
这意味着至少两次归约与同步
3.2.2 重写等价
将上式等价重排为: \(\nabla x_i = \frac{w_i \nabla y_i}{\sigma(x)} ;+; \alpha \sum_j w_j \nabla y_j ;+; \beta \sum_j w_j \nabla y_j x_j\) 其中 $$ \alpha=\frac{[x_i-\mu(x)],\mu(x)-\sigma(x)^2}{m,\sigma(x)^3}, \qquad \beta=\frac{\mu(x)-x_i}{m,\sigma(x)^3}.
$$ 关键点:
-
将涉及 $\hat{x}_j$ 的项改写为只依赖两类更“原子”的内积:
- $S_1=\sum_j w_j \nabla y_j$
- $S_2=\sum_j w_j \nabla y_j x_j$
-
对于每个归一化行(或向量)仅需在一次遍历中同时累加出 $S_1,S_2$ 两个标量,然后按元素用上式合成 $\nabla x_i$
- 右图的红色虚线框“Inner Prod”对应的就是在一个 kernel 内同时计算 $S_1$ 和 $S_2$ 两个内积
- 随后进入单个 element-wise 阶段完成最终组合
- 一次同步即可完成两个内积的归约
3.2.3 优化点
- 原式需要分别归约两次(甚至三次:还要用到 $\mu,\sigma$,重写后把需要的统计量组织为可在一次归约中并行累加的两路内积
- 访存更少:一次读入 $(w_j,\nabla y_j,x_j)$ 即可同时更新 $S_1,S_2$
- 同步更少:从“两次以上同步”降为“一次同步”,对应 kernel 更短、调度/屏障更少
3.3 重写 softmax 前向(行级归约的单 kernel 实现)
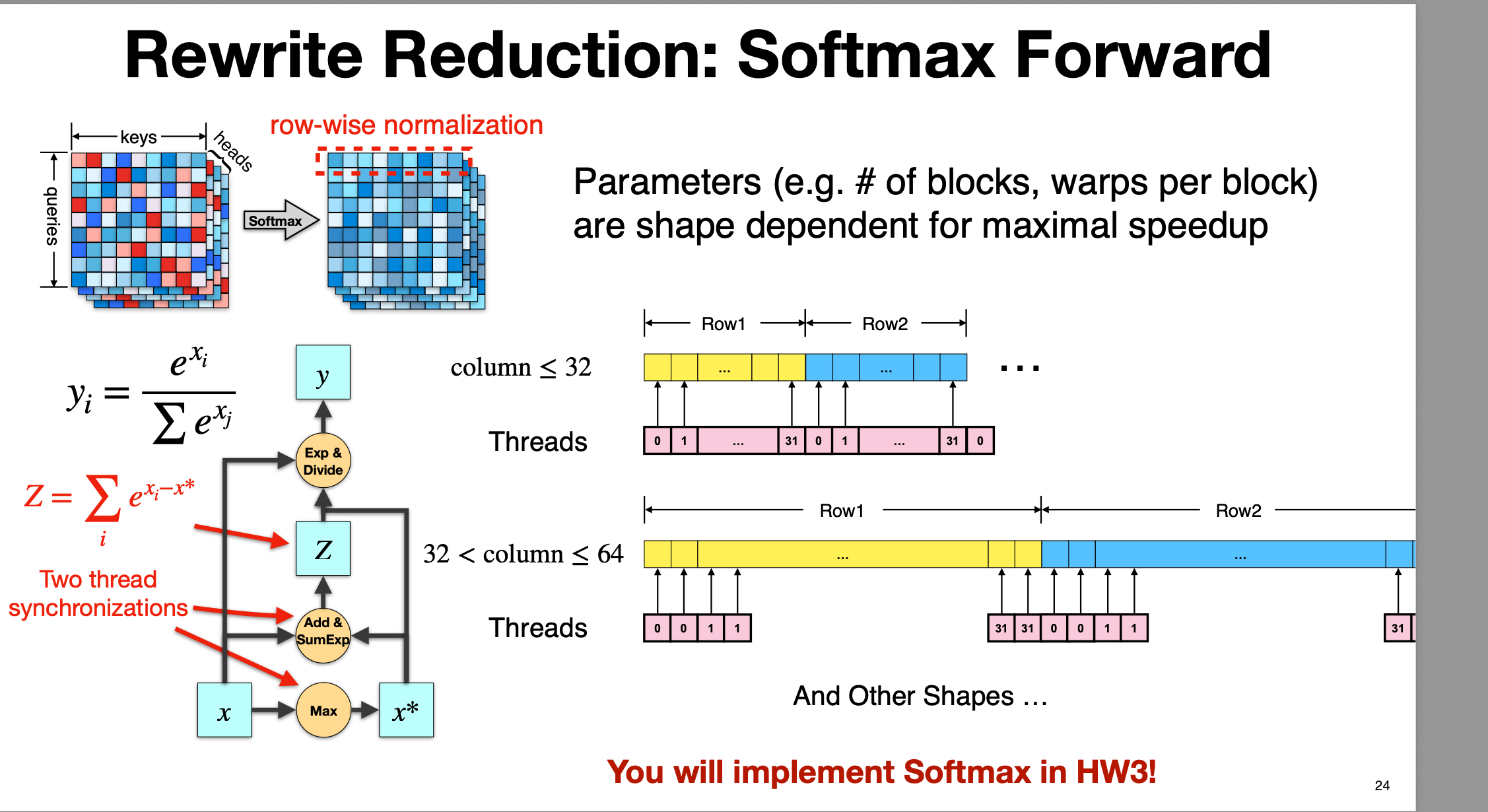 通过重写归约(Rewrite Reduction)来减少线程同步开销、提高 GPU 并行效率
通过重写归约(Rewrite Reduction)来减少线程同步开销、提高 GPU 并行效率
3.3.1 重写前
Softmax 公式: \(y_i = \frac{e^{x_i}}{\sum_j e^{x_j}}\) 为了数值稳定性,一般会写成: \(y_i = \frac{e^{x_i - x^*}}{\sum_j e^{x_j - x^*}}, \quad x^* = \max_j x_j\)
计算流程:
- Max reduction:找出当前行(row)的最大值 $x^*$,用于数值稳定。
- Exp & Sum reduction:对 $\exp(x_i - x^)$ 做一次归约求和,得到 (Z = \sum_i \exp(x_i - x^))。
- Exp & Divide:对每个元素计算 (\exp(x_i - x^*) / Z)。
这个流程中,至少需要:
- 1 次 reduction(Max)
- 1 次 reduction(SumExp)
- 2 次线程同步(图中红色标注 “Two thread synchronizations”)
每一行(row)执行 softmax 都是这种三步结构。在 Attention 中,softmax 是对 [queries × keys] 的矩阵在行维度上进行归一化(row-wise normalization)
3.3.2 重写后
重写计算和组织线程,在一个 kernel 内高效完成 max、exp、sum 和归一化,减少同步、提升并行。
关键点:
- Softmax 是 按行(row-wise)归一化。
- 每一行都可以由一个线程块处理。
-
利用 warp/block 内的 reduction 技巧,在一个 kernel 内完成:
- Max 计算
- 减去 max 并计算 exp
- SumExp 归约
- 归一化
- 不再需要多个 kernel 来分别做 max → exp → sum → divide。
3.3.3 不同列数的处理
当行的长度(column数)不同情况下的线程分配策略。
-
当 column ≤ 32(小于一个 warp)时,每一行可以由 一个 warp 直接完成,warp 内使用 warp shuffle 实现 max 和 sum 两次归约,无需 block-level 同步。
- 例如,Row1 分配给 32 个线程中的前 N 个,每个线程处理一个元素,warp 内用 shuffle 归约计算 max 和 sum。
-
当 32 < column ≤ 64 时,每一行可能由一个 block 的多个 warp 来协作,需要做 block 内 reduction(例如共享内存 + warp 归约)。
- 例如 Row1 由 2 个 warp 处理,需要一次 block-level 的同步。
-
其他更大列数的情况(And Other Shapes)则按类似原则扩展,分块并行、按行处理。
关键在于:
- 行内(row)是计算和归约的基本单元。
- 不同长度的行需要不同的线程/warp/block 配置 来获得最大吞吐
3.3.4 优化对比
| 项目 | 标准实现 | Rewrite 实现 |
|---|---|---|
| Reduction 次数 | 2(max + sumexp) | 2(但可在同一 kernel 内完成) |
| 同步次数 | 多个 kernel,多次同步 | 1 个 kernel,warp/block 内有限同步 |
| 内存访问 | 多次读写中间结果 | 一次读入,一次写出,中间在寄存器/共享内存中完成 |
| 调度开销 | 多 kernel launch | 1 kernel launch |
| 并行方式 | 行级别,多 kernel | 行级别,单 kernel,warp 优化 |
3.3.5 代码实现
https://github.com/bytedance/lightseq/blob/master/lightseq/csrc/kernels/cuda/softmax_kernels.cu
通过 模版进行 parameter tuning
template <typename T, int block_dim, int ele_per_thread>
__global__ void ker_attn_softmax(T *inp, const T *attn_mask, int from_len,
int to_len, bool mask_future)
template <typename T, int block_dim, int ele_per_thread>
__global__ void ker_attn_softmax_lt32(T *inp, const T *attn_mask, int from_len,
int to_len, bool mask_future)
通过 if else 判断,进行不同的 kernel launch
template <typename T>
void launch_attn_softmax_bw(T *out_grad, const T *soft_inp, int rows,
int softmax_len, cudaStream_t stream) {
const int warps_per_block = 4;
// rows = batch_size * nhead * from_len
dim3 grid_dim(rows / warps_per_block);
dim3 block_dim(WARP_SIZE, warps_per_block);
if (softmax_len <= 32)
ker_attn_softmax_bw<T, 1>
<<<grid_dim, block_dim, 0, stream>>>(out_grad, soft_inp, softmax_len);
else if (softmax_len <= 64)
ker_attn_softmax_bw<T, 2>
<<<grid_dim, block_dim, 0, stream>>>(out_grad, soft_inp, softmax_len);
else if (softmax_len <= 128)
ker_attn_softmax_bw<T, 4>
<<<grid_dim, block_dim, 0, stream>>>(out_grad, soft_inp, softmax_len);
else if (softmax_len <= 256)
ker_attn_softmax_bw<T, 8>
<<<grid_dim, block_dim, 0, stream>>>(out_grad, soft_inp, softmax_len);
else if (softmax_len <= 384)
ker_attn_softmax_bw<T, 12>
<<<grid_dim, block_dim, 0, stream>>>(out_grad, soft_inp, softmax_len);
else if (softmax_len <= 512)
ker_attn_softmax_bw<T, 16>
<<<grid_dim, block_dim, 0, stream>>>(out_grad, soft_inp, softmax_len);
else if (softmax_len <= 768)
ker_attn_softmax_bw<T, 24>
<<<grid_dim, block_dim, 0, stream>>>(out_grad, soft_inp, softmax_len);
else if (softmax_len <= 1024)
ker_attn_softmax_bw<T, 32>
<<<grid_dim, block_dim, 0, stream>>>(out_grad, soft_inp, softmax_len);
else if (softmax_len <= 2048)
ker_attn_softmax_bw<T, 64>
<<<grid_dim, block_dim, 0, stream>>>(out_grad, soft_inp, softmax_len);
else
throw std::runtime_error(
std::string(
"Special sequence length found in softmax backward, seq_len: ") +
std::to_string(softmax_len));
}
4 混合精度策略
4.1 动机
- 现代 GPU 支持 FP16/FP8(H100)。
- 收益
- 可以减少显存,增大batch size
- 可以更快传输数据
- 可以有更高的FLOPS
4.2 混合策略(为什么不全部采用低精度)
-
forward 和 backward 可以用fp16 /fp8
-
优化器必须用fp32
- FP16 / FP8 的动态范围有限,不能精确地累计很多次梯度更新,会导致数值不稳定、训练不收敛
- 例如: FP16 的最小可表示数约为 6e-8,梯度如果非常小,可能在累计时就变成 0
NVIDIA APEX 库提供自动混合精度(AMP)支持
-
自动把模型的计算分为 FP16 与 FP32 区域。
-
自动管理 loss scaling(避免梯度下溢)。
-
针对常见算子(如 Conv、GEMM、LayerNorm 等)做混合精度优化。
-
使用方式简单,一般只需包一层 amp.initialize(model, optimizer) 即可。
-
这大大简化了混合精度训练的实现复杂度,不用手工改每一层的精度类型
但对超大 LLM 的细粒度显存优化仍需工程化改造
4.3 混合精度的加速
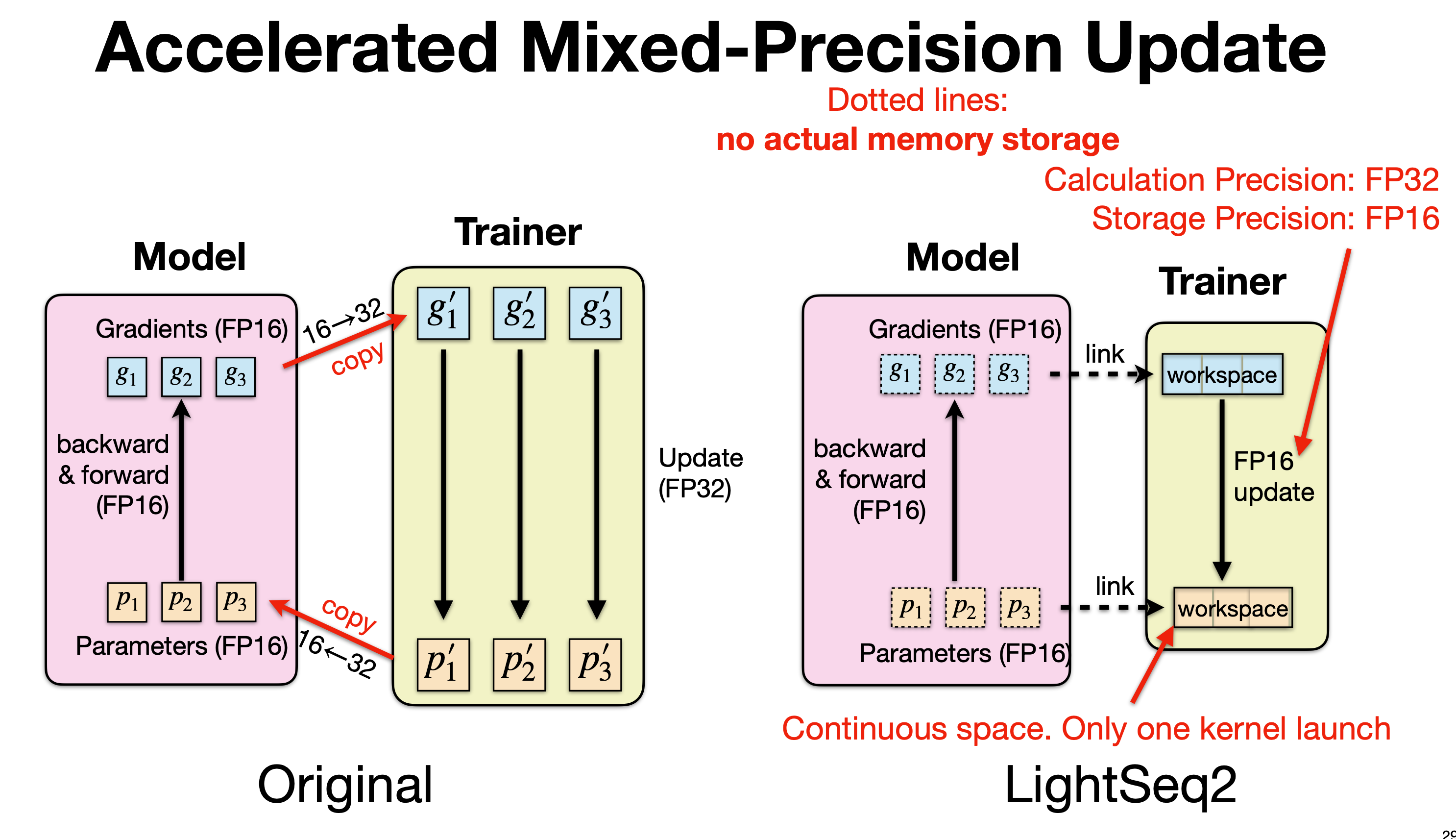
这张图是在讲 混合精度更新(Mixed-Precision Update) 的两种实现方式: 左边是 原始/传统 AMP 实现,右边是 LightSeq2 的加速实现。核心区别在于梯度与参数在 FP16↔FP32 之间的处理方式,LightSeq2 通过消除不必要的内存拷贝与 kernel 启动开销来显著提速。
4.3.1 优化前
常规的混合精度训练流程(比如 NVIDIA APEX AMP):
1. FP16 前后向计算
- 模型参数 ( p_1, p_2, p_3 ) 存储在 FP16 中。
- 前向(forward)和反向(backward)都使用 FP16 精度,计算得到 FP16 的梯度 ( g_1, g_2, g_3 )
2. FP16 → FP32 拷贝
-
在执行梯度更新之前:
- 梯度会被从 FP16 拷贝并转换成 FP32,得到 ( g’_1, g’_2, g’_3 )。
- 参数也会从 FP16 拷贝并转换成 FP32,得到 master 参数 ( p’_1, p’_2, p’_3 )。
这个转换是必要的,因为:
- 优化器(Adam / SGD)更新需要 FP32 的数值稳定性。
- 通常梯度很小,如果不转 FP32,累积时会下溢。
3. Trainer 中的 FP32 更新
- 所有更新(例如 Adam 算法)都在 FP32 空间进行。
- 更新完之后,再把 FP32 参数 cast 回 FP16,传回模型用于下一轮前向。
4. 开销问题
-
每次迭代都要进行:
- 梯度从 FP16→FP32 的 拷贝 + 转换
- 参数从 FP16→FP32 的 拷贝 + 转换
- 每个参数 tensor 需要分别调用 kernel 进行拷贝,kernel launch 次数多。
- 对于 LLM(上百亿参数),这种频繁的转换会成为 显著的性能瓶颈,尤其是在梯度更新步骤。
4.3.2 LightSeq2 优化实现
优化重点是——避免多次内存拷贝 + 合并 kernel 调用,实现加速
1. 梯度和参数依然存储为 FP16
- 计算(forward/backward)依旧在 FP16 上完成。
- 但关键是:梯度和参数不会再被分别拷贝出来存 FP32 的副本。
2. Workspace + 链接(link)机制
图中右侧 Trainer 部分的「workspace」是一个连续的内存块,用于直接处理更新:
-
梯度和参数的 FP16 数据 与 workspace 之间是 link(虚线):
- 表示不进行实际的内存复制(no actual memory storage)。
- 通过指针链接,Trainer 直接访问 Model 的 FP16 数据位置。
-
Trainer 使用一个 连续的 workspace 存储更新所需的中间信息,而不是为每个参数单独分配一段空间
3. FP16 update 内核
-
LightSeq2 使用一个特殊的 kernel,直接在 FP16 上完成参数更新:
- 例如 fused kernel:在一次 kernel launch 里,完成 FP16 → FP32(在寄存器中)、FP32 计算、再 cast 回 FP16。
- 不需要真正拷贝大块参数到 FP32 buffer。
-
这种方式把原来多次 kernel 调用 + 多次内存拷贝,合并成一次连续操作:
- “Continuous space. Only one kernel launch”
4.3.3 优化对比
| 项目 | Original | LightSeq2 |
|---|---|---|
| 梯度/参数转换 | 需要 FP16→FP32 显存拷贝 | 无拷贝,仅链接 |
| 内存使用 | 多个 buffer,分散 | 一个 workspace,连续 |
| kernel 调用 | 多次,小粒度 | 一次,大粒度 |
| 性能瓶颈 | 拷贝 + kernel launch overhead | 极大减少 |
这种优化对于大模型训练(例如数十亿参数)尤其重要:
- 梯度更新步骤的显存带宽占用和 kernel launch overhead 明显降低。
- 更新速度提升,有时能达到 10~20% 的 step time 优化。
5 自注意力反向显存复用
(Memory Reuse GPU Memory Management for Self Attention Backward)
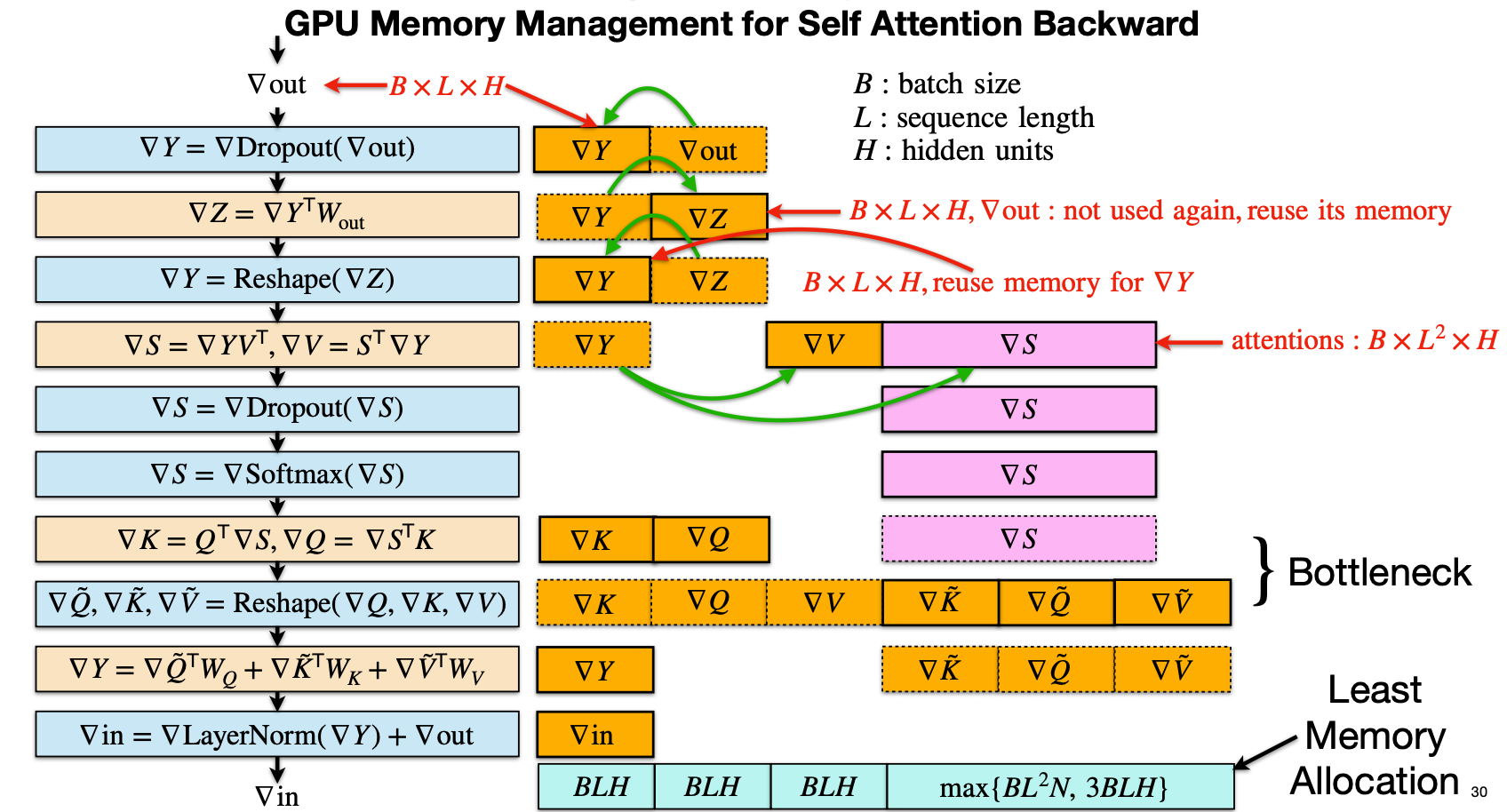
对Transformer 自注意力(Self Attention)反向传播阶段的显存优化方法,通过内存复用(Memory Reuse)来显著降低中间梯度张量的显存占用,从而提升大模型训练的效率。
5.1 反向传播中各个张量的内存开销
图左侧的蓝色和黄色模块展示了自注意力反向传播的标准计算流程,从输出梯度 ( $nabla V_{\text{out}} $ 开始,逐步反向计算各个梯度 主要张量的形状如下:
- $ B $:batch size
- $ L $:序列长度
- $ H $:隐藏维度(hidden size)
| 张量名称 | 尺寸复杂度 |
|---|---|
| $ \nabla V_{\text{out}} $、$ \nabla Y $、$ \nabla Z $ | $ B \times L \times H $ |
| $ \nabla S $(注意力矩阵梯度) | $ B \times L^2 \times H $(或更准确地说是 $ B \times \text{heads} \times L \times L )$ |
| $ \nabla Q, \nabla K, \nabla V $ | $ B \times L \times H $ |
其中 $ \nabla S $ 是最大开销项,因为它对应于注意力矩阵,大小随 ( L^2 ) 增长,是主要显存瓶颈。
5.2 内存复用策略
图中橙色和绿色箭头标出了哪些中间张量可以被回收再利用:
-
复用 $\nabla V_{\text{out}}$ 的内存来存 $\nabla Y$
- 在 Dropout、W_out 反向计算之后,$\nabla V_{\text{out}}$ 不再被使用
- 它的内存大小为 $B \times L \times H$,可以直接复用这块空间来存 $\nabla Y$
-
复用 $\nabla Z$ 的内存来存后续的 $\nabla Y$
- 计算 $\nabla Z = \nabla Y^\top W_{out}$ 后,$\nabla Z$ 也不再需要
- 可以将这块 $B \times L \times H$ 的空间再次用于 $\nabla Y$ 的 reshape 或其他中间结果
-
$\nabla S$ 的空间在 Dropout 与 Softmax 反向计算之间复用
- $\nabla S$ 在计算时先经过 Dropout,再经过 Softmax 的梯度
- 同一块空间在两个阶段可以被循环利用,不需要两份副本
-
$\nabla V, \nabla Q, \nabla K$ 的存储也通过复用避免额外的拷贝
- 比如 $\nabla V$ 计算完后可以重用为 $\nabla Q$ 的中间存储。
通过这些策略,多个中间梯度不再各自占用独立内存,而是在不同时间阶段复用同一块内存区域,达到节省显存的目的。
5.3 显存瓶颈与复用效果
图中右侧标出了两类区域:
-
Bottleneck(瓶颈): 主要是 $\nabla S$ 阶段,因为其尺寸为 $ B \times L^2 \times H $,当 L 较大时(如几千 token),这是反向传播中占用显存最多的部分。
-
Least Memory Allocation(最小内存分配): 通过上述内存复用,整个自注意力反向传播过程中,显存的最大占用被控制在: $ \max{B \times L^2 \times N,\ 3 \times B \times L \times H} $ 其中 $ N $ 是注意力头数(number of heads)。 相较于 naive 实现,省去了大量不必要的中间 buffer 分配。
5.4 实际意义
在大模型训练中,自注意力反向传播是显存占用最集中的部分之一。 如果不做内存复用,每一层都可能临时分配数十到上百 MB 的中间梯度张量,在数百层 Transformer 堆叠时,显存压力极大
通过这种内存复用策略,可以在不改变计算逻辑的前提下:
- 显著降低峰值显存占用
- 提高 GPU 内存利用率
- 为更大的 batch size 或更长的序列长度腾出空间
6 加速策略总结
主要思路:
-
前向和反向计算的高效算子kernel
-
高效的参数更新
-
高效的显存管理