1 模型并行训练概念(Model Parallel Training)
模型并行(Model Parallelism):将模型的计算(前向传播 / 反向传播 / 参数更新)分布到多个 GPU 上执行。
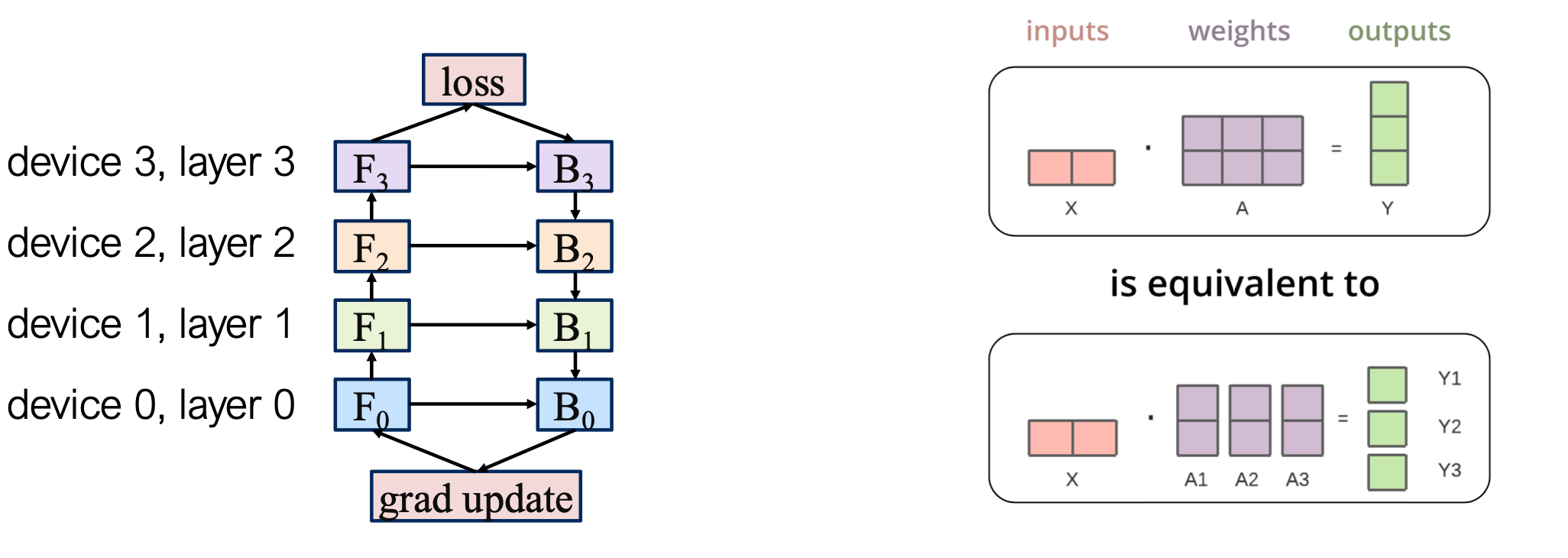
2 流水线PP并行
2.1 朴素模型并行(Naïve Model Parallel)
最原始的模型并行方式是:将模型的不同层分布到不同 GPU 上执行。
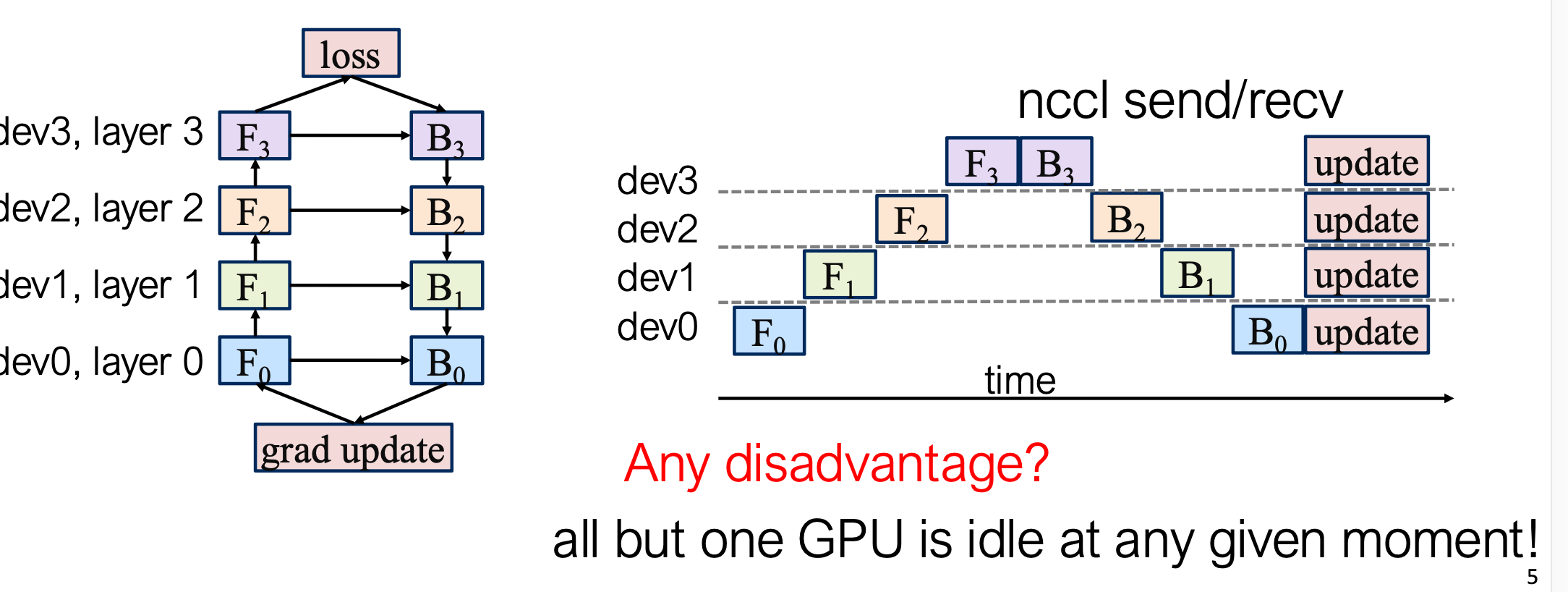
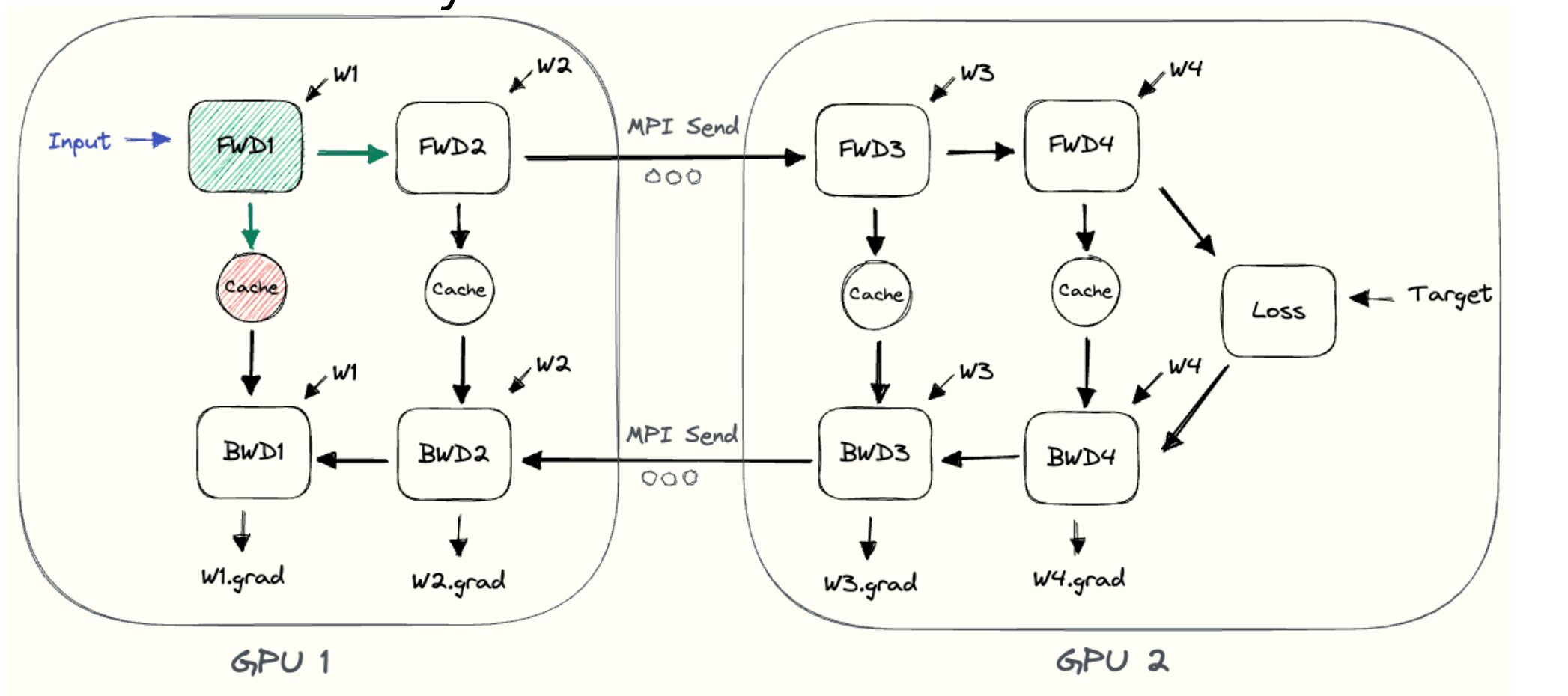
参考: https://siboehm.com/articles/22/pipeline-parallel-training
在模型定义的时候,针对于层数进行拆分
class ModelParallelResNet50(ResNet):
def __init__(self, *args, **kwargs):
super(ModelParallelResNet50, self).__init__(
Bottleneck, [3, 4, 6, 3], num_classes=num_classes, *args, **kwargs)
self.seq1 = nn.Sequential(
self.conv1,
self.bn1,
self.relu,
self.maxpool,
self.layer1,
self.layer2
).to('cuda:0')
self.seq2 = nn.Sequential(
self.layer3,
self.layer4,
self.avgpool,
).to('cuda:1')
self.fc.to('cuda:1')
def forward(self, x):
x = self.seq2(self.seq1(x).to('cuda:1'))
return self.fc(x.view(x.size(0), -1))
局限性
- GPU 利用率低:同一时刻只有一个 GPU 在计算,其余处于空闲
- 计算与通信无法重叠:传输中间结果时 GPU 处于空闲状态
- 内存需求高:首个 GPU 需缓存所有激活值,直到整个 batch 完成
2.2 GPipe:经典流水线并行方案
2.2.1 核心思想
核心思想:将一个 batch 拆分成多个 micro-batch,以流水线方式在不同 GPU 间流动。
-
一个 batch 的大小通常由 GPU 的显存容量以及单个样本在前向/反向传播中所需的显存决定, 通常尽可能大,以充分利用 GPU 显存。
-
一个 micro-batch 则可以更小
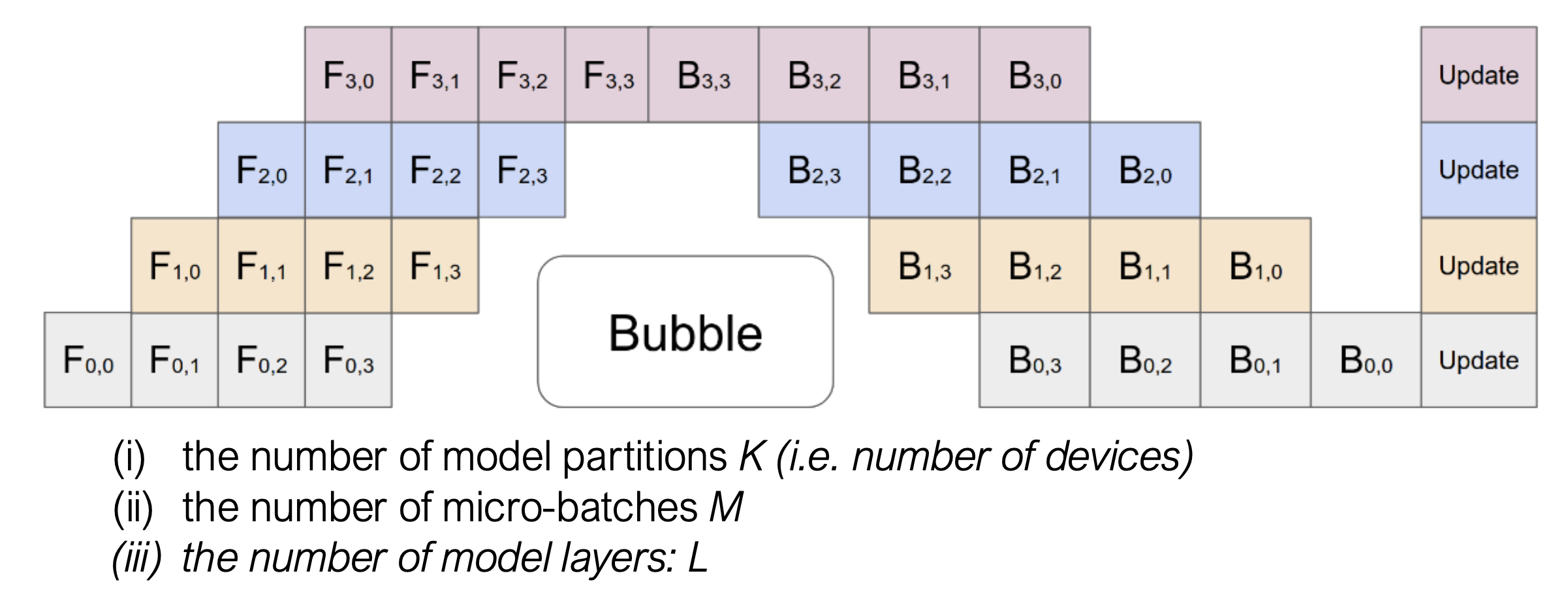
方块里的字母和数字是有特定含义的:
- $F_{i,j}$ (Forward):代表第 $i$ 个设备(Stage/Device)正在处理第 $j$ 个微批次(Micro-batch)的前向传播。
- 例如:$F_{0,0}$ 是设备 0 处理微批次 0。
- $B_{i,j}$ (Backward):代表第 $i$ 个设备正在处理第 $j$ 个微批次的反向传播。
- Update:代表在所有计算完成后,进行参数更新(Optimizer Step)。
这张图清晰地体现了 GPipe 的工作方式:
- 全前向阶段:设备会连续把所有微批次(0, 1, 2, 3)的前向传播做完。
- 强制等待:注意看图中,最后一个设备(最顶上的 Stage 3)必须等 $F_{3,3}$ 算完,才能开始算 $B_{3,3}$。
- 全反向阶段:一旦开始反向,就连续把所有微批次的反向做完。
图中中间那个巨大的白色区域标着 “Bubble”。这是流水线并行的痛点:
- 产生原因:
- 启动开销:当设备 0 在算 $F_{0,1}$ 时,设备 3 还在空等数据传过来。
- 排空开销:在 GPipe 这种模式下,前向全部结束后,后面的设备(如 Stage 0, 1)必须等待最后面的设备算出反向梯度传回来。
- 计算公式:在 GPipe 中,气泡的大小(浪费的时间)大约是 $(K-1)$ 个前向 + $(K-1)$ 个反向的时间(其中 $K$ 是设备数量)。
这个图能解释为什么 GPipe 非常吃显存:
- 观察设备 0(最下方):它最早算完了 $F_{0,0}$,但是它必须等很久(跨过整个 Bubble 区域)才能开始算 $B_{0,0}$。
- 后果:为了算 $B_{0,0}$,设备 0 必须把 $F_{0,0}$ 产生的中间激活值(Activations)一直存在显存里。同理,它还得存 $F_{0,1}, F_{0,2}, F_{0,3}$ 的激活值。
- 结论:微批次数量 $M$ 越大,显存占用越高。
参考论文: [1] Huang, Yanping, et al. “Gpipe: Efficient training of giant neural networks using pipeline parallelism.” NeurIPS 2019.
2.2.2 梯度检查点
减少流水线并行的显存开销,其实主要是重计算,用计算换显存
前向传播阶段:每个 GPU 仅保存输出激活值。 反向传播阶段:每个阶段重新计算自己的前向函数 $F_k$
2.2.2.1 Vanilla Backprop(普通反向传播)
显存占用:O(n)
-
因为在前向传播时,网络中每一层的中间激活值(activation)都被保存下来
-
在反向传播计算梯度时直接使用这些缓存的激活
-
所以显存随层数线性增长
计算量:O(n)
- 每层在 forward 计算一次,在 backward 计算一次,因此总体是线性复杂度
优点: 快(无需重复计算) 缺点: 占用大量显存,难以在大模型上训练。
2.2.2.2 Memory-poor Backprop(节省显存的反向传播 / 梯度检查点)
显存占用:O(1)
- 在前向传播阶段不保存所有中间激活,只保留少量(例如 checkpoint 的节点输出)。
- 在反向传播时,需要重新计算(recompute)部分前向结果。
- 因此显存占用几乎与层数无关。
计算量:O(n²)
- 因为反向传播时要多次重新执行前向计算(每次重算部分子网络的 forward),
- 导致计算开销从线性上升为平方级别。
2.2.2.3 对比
| 算法类型 | 显存占用 | 计算量 | 特点 | | ——————– | —— | ——– | ——- | | Vanilla Backprop | $O(n)$ | $O(n)$ | 快但显存高 | | Checkpointing | $O(1)$ | $O(n^2)$ | 显存低但需重算 |
参考;
https://github.com/cybertronai/gradient-checkpointing
Chen, Tianqi, et al. “Training deep nets with sublinear memory cost.” arXiv preprint arXiv:1604.06174 (2016).
2.3 PP 并行弊端分析
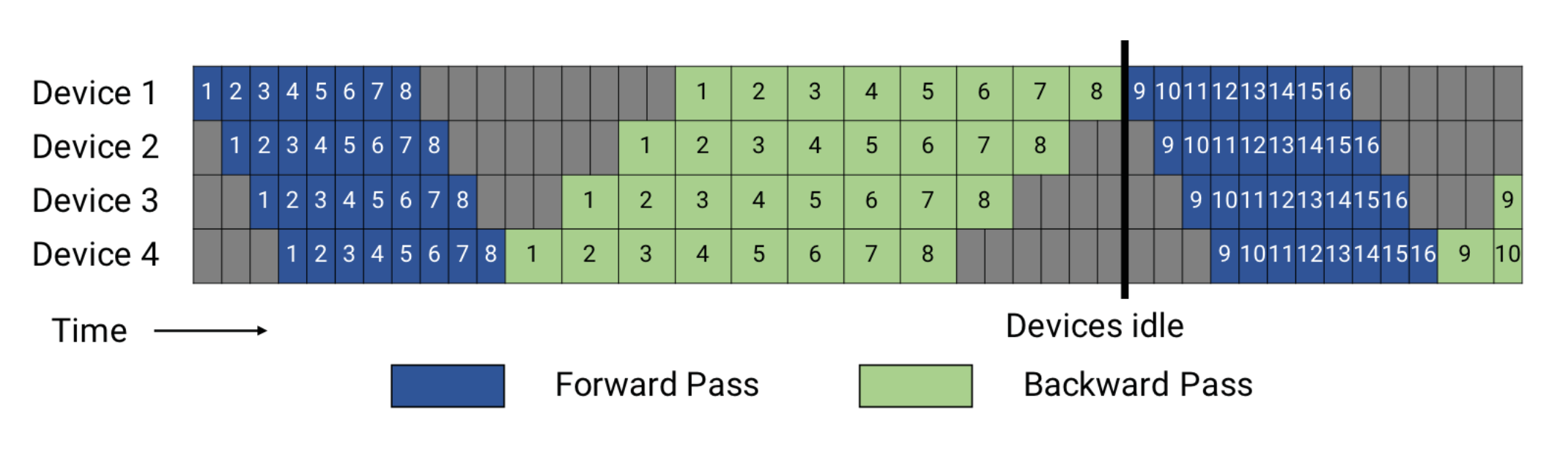
图中的蓝色方块 1 代表了一个Micro batch的数据前向计算过程,一共有8个蓝色方块 ,代表着这次任务 GBS/ MBS=8
Pipeline Flush 是完成了一个Batch
我们可以合理估算 Backward时间是Forward 2倍
主要原因可以从数学计算(矩阵乘法的次数)的角度来理解:
- 前向传播(1次矩阵乘法)
在前向传播中,对于模型的一个线性层(Layer),我们主要做一件事:
- 计算输出:用输入 $X$ 和权重 $W$ 相乘,得到激活值 $Y$。
- 公式:$Y = X \cdot W$
- 这里只涉及 1次 核心的矩阵乘法运算。
- 反向传播(2次矩阵乘法) 在反向传播中,为了实现链式法则,设备需要完成 两项 不同的梯度计算任务:
- 任务 A:计算对输入的梯度(Grad_X)
- 为了把误差传给“上一个”设备(前一层),需要计算 $\frac{\partial Loss}{\partial X}$。
- 这涉及一次矩阵乘法:$\text{Grad_X} = \text{Grad_Y} \cdot W^T$
- 任务 B:计算对权重的梯度(Grad_W)
- 为了更新当前层的参数,需要计算 $\frac{\partial Loss}{\partial W}$。
- 这涉及另一次矩阵乘法:$\text{Grad_W} = X^T \cdot \text{Grad_Y}$
-
等待时间(Bubble)与内存需求: 为了计算梯度(后向传播),每个阶段需要其对应的前向传播过程中产生的激活值,即填充/排空 阶段的 GPU空间
-
In-Flight)的微批次: 由于pipeline 的填充和排空(filling and draining),在任何给定时间点,某些微批次可能已经完成了前向传播(生成了激活值),但尚未开始或完成后向传播。这些就是“in-flight”的微批次, 反向传播未开始的前向激活需保留在显存中
- 巨大的内存开销: 必须在 GPU 内存中保留所有这些“in-flight”微批次产生的全部激活值,直到它们相应的后向传播完成并释放内存为止。如果“in-flight”微批次的数量很大(如示例中的 8 个),则所需的内存会显著增加,甚至可能超过设备的可用内存,这就是主要的内存瓶颈
总结:开 PP 虽能加速,但内存与调度负担显著增加
2.4 1F1B Flush 优化策略
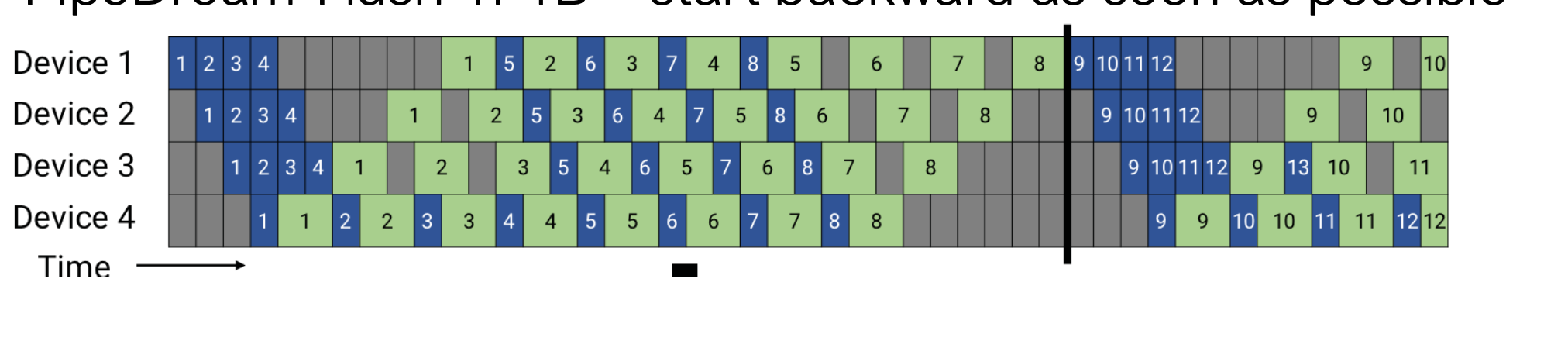
思路:在前向传播还未全部完成时,提前启动反向传播(即“尽早 backward”)
效果:显著减少 in-flight 激活值数量。 例如:若 $1B = 2F$,则最大仅有 4 个微批次同时驻留显存,而 GPipe 为 8 个
2.5 更进一步优化 vpp/pp chunk/interleaved pp
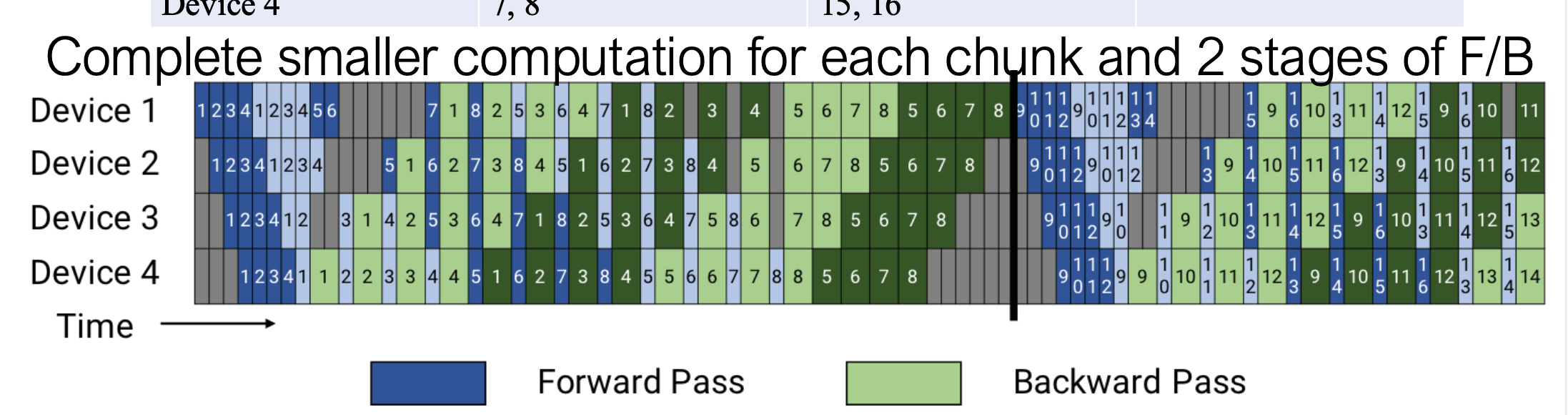
主要是通过vpp/interleaved pp,在PP分stage 的基础上,在每个stage 里再进行切分,不增加rank
2.5.1 为什么同一个设备上会有两个“1”?(例如 Device 1)
在普通的流水线(上方图)中,Device 1 算完微批次 1 就传给 Device 2 了,它自己不再管微批次 1。
但在交错式(Interleaved)中:
vpp size = 2
- 深蓝色方块 1:代表 Device 1 在处理微批次 1,使用的模型是第一部分 chunk1(比如第 1-10 层)。
- 浅蓝色方块 1:代表 Device 1 再次处理微批次 1,但此时使用的模型是第二部分 chunk 2(比如第 41-50 层)。
2.5.2 微批次 1 的“旅行路线”变长了
在下图中,你可以追踪一下 微批次 1 的流动路径:
- Device 1 算深蓝 1(模型第 1 块)$\rightarrow$ 传给 Device 2。
- Device 2 算深蓝 1(模型第 2 块)$\rightarrow$ 传给 Device 3。
- Device 3 算深蓝 1(模型第 3 块)$\rightarrow$ 传给 Device 4。
- Device 4 算深蓝 1(模型第 4 块)$\rightarrow$ 又传回给 Device 1!
- Device 1 算浅蓝 1(模型第 5 块)$\rightarrow$ 传给 Device 2。
- …以此类推,直到 Device 4 算完浅蓝 1(模型第 8 块)。
3. 颜色和数字的真正含义
- 数字(1, 2, 3…):依然代表哪一个微批次的数据。
- 颜色深浅(Dark/Light):代表哪一个模型分块(Chunk)。
- 深色 = 该设备持有的“第一阶段”模型。
- 浅色 = 该设备持有的“第二阶段”模型。
只是在交错式调度下,同一个 microbatch (比如 1 号) 会分两次“路过”同一个设备。第一次路过时,设备用模型的前段(深色)去算它;第二次路过时,设备用模型的后段(浅色)去算它。
就是为了让 Device 1 算完“深色 1”后,不用等太久就能立刻开始算“深色 2”、“深色 3”……并且在 Device 4 还没忙完的时候,Device 1 就能插空开始算“浅色 1”。这样就把等待的灰色气泡时间给塞满了,提高了 GPU 利用率。
在传统的管道并行中,不同的模型阶段(Stages)通常分配给不同的物理设备(GPU 0 负责 Stage 1,GPU 1 负责 Stage 2 等)。交错阶段指的是让同一个物理设备(例如 GPU 0)负责多个不连续的阶段(例如 Stage 1 和 Stage 4)。
-
缓解设备差异: 如果某些 GPU 性能较差,可以将计算量较小的阶段或交错分配给它们,以更好地利用所有硬件资源。
-
解决管道气泡: 可以在一个设备处理 Stage A 的后向传播时,同时处理 Stage B 的前向传播,从而更好地填补管道中的空闲时间,进一步减少等待,提高硬件利用率
参考论文: Efficient Large-Scale Language Model Training on GPU Clusters Using Megatron-LM, Narayanan et al. (SC 2021)
2.6 GPipe 实现示例
仓库地址:https://github.com/siboehm/shallowspeed
class GPipeSchedule(Schedule):
"""
GPipe调度器:实现经典的“先全F后全B”管道并行策略
"""
def steps(self):
# 步骤 0: 梯度清零
yield [ZeroGrad()]
# STAGE 1: FWD all μBatches 对所有微批次 (μBatches) 进行前向传播 (FWD)
for mubatch_id in range(self.num_micro_batches):
yield self.steps_FWD_mubatch(mubatch_id)
# STAGE 2: BWD all μBatches 对所有微批次 (μBatches) 进行后向传播 (BWD),注意是逆序进行
for mubatch_id in reversed(range(self.num_micro_batches)):
yield from self.steps_BWD_mubatch(mubatch_id)
# updating the weights is the last step of processing any batch 更新权重
yield [OptimizerStep()]
def steps_BWD_mubatch(self, mubatch_id):
"""定义单个微批次的后向传播步骤 (BWD)"""
cmds = []
# 如果是最后一个阶段(模型的尾部):
if self.is_last_stage:
# 加载目标值(标签),用于计算损失和起始梯度
cmds.append(LoadMuBatchTarget(mubatch_id=mubatch_id, buffer_id=0))
else:
# 接收来自下游阶段(模型更深层)的梯度(损失对输出的梯度)
cmds.append(RecvOutputGrad(buffer_id=0))
# 如果是第一个微批次(通常是最后一个 BWD 步骤):
if self.is_first_mubatch(mubatch_id):
# interleaved backprop & AllReduce during last μBatch of BWD
# 在最后一个微批次的 BWD 过程中,交错执行反向传播和 AllReduce
cmds.append(BackwardGradAllReduce(buffer_id=0, mubatch_id=mubatch_id))
else:
# 执行反向传播,并将梯度累加起来(Accumulation)
cmds.append(BackwardGradAcc(buffer_id=0, mubatch_id=mubatch_id))
# 如果不是第一个阶段(模型的头部):
if not self.is_first_stage:
# 将计算出的梯度(损失对输入的梯度)发送给上游阶段(模型更浅层)
cmds.append(SendInputGrad(buffer_id=0))
yield cmds
def steps_FWD_mubatch(self, mubatch_id):
"""定义单个微批次的前向传播步骤 (FWD)"""
cmds = []
# 如果是第一个阶段(模型的头部):
if self.is_first_stage:
# 加载输入数据(特征)
cmds.append(LoadMuBatchInput(buffer_id=0, mubatch_id=mubatch_id))
else:
# 接收来自上游阶段(模型更浅层)的激活值
cmds.append(RecvActivations(buffer_id=0))
# 执行前向传播计算
cmds.append(Forward(buffer_id=0, mubatch_id=mubatch_id))
# the last stage just discards the output of its `forward()` pass since
# it's not necessary for running BWD. The last stage just needs the target values
# (loaded from disk) and the activations (cached inside the `Module`s) for BWD.
# 如果不是最后一个阶段:
# 将输出的激活值发送给下游阶段(模型更深层)
# 注意:最后一个阶段会丢弃其 forward() 输出,因为它只需要 target 值和内部缓存的激活值
if not self.is_last_stage:
cmds.append(SendActivations(buffer_id=0))
return cmds
2.7 PyTorch 官方 PP 实现
PyTorch 提供原生 API:
torch.distributed.pipelining
2.7.1 两个阶段
-
构建阶段(PipelineStage)
- 手动划分模型层。
- 或使用自动划分工具。
-
调度阶段(PipelineSchedule)
- 执行微批次调度。
2.7.2 模型构建示例
class Transformer(nn.Module):
def __init__(self, model_args: ModelArgs):
super().__init__()
self.tok_embeddings = nn.Embedding(...)
# Using a ModuleDict lets us delete layers without affecting names,
# ensuring checkpoints will correctly save and load.
self.layers = torch.nn.ModuleDict()
for layer_id in range(model_args.n_layers):
self.layers[str(layer_id)] = TransformerBlock(...)
self.output = nn.Linear(...)
def forward(self, tokens: torch.Tensor):
# Handling layers being 'None' at runtime enables easy pipeline splitting
h = self.tok_embeddings(tokens) if self.tok_embeddings else tokens
for layer in self.layers.values():
h = layer(h, self.freqs_cis)
h = self.norm(h) if self.norm else h
output = self.output(h).float() if self.output else h
return output
2.7.3 管道与调度示例
from torch.distributed.pipelining import PipelineStage
with torch.device("meta"):
assert num_stages == 2, "This is a simple 2-stage example"
# we construct the entire model, then delete the parts we do not need for this stage
# in practice, this can be done using a helper function that automatically divides up layers across stages.
model = Transformer()
if stage_index == 0:
# prepare the first stage model
del model.layers["1"]
model.norm = None
model.output = None
elif stage_index == 1:
# prepare the second stage model
model.tok_embeddings = None
del model.layers["0"]
from torch.distributed.pipelining import PipelineStage
stage = PipelineStage(
model,
stage_index,
num_stages,
device,
)
管道构建,拆分stage 后实例化 PipelineStage
from torch.distributed.pipelining import ScheduleGPipe
# Create a schedule
schedule = ScheduleGPipe(stage, n_microbatches)
# Input data (whole batch)
x = torch.randn(batch_size, in_dim, device=device)
# Run the pipeline with input `x` # `x` will be divided into microbatches automatically
if rank == 0:
schedule.step(x)
else:
output = schedule.step()
参考文档:https://pytorch.org/docs/main/distributed.pipelining.html
3 张量并行(Tensor Parallelism, TP)
核心思想:矩阵按列 / 行拆分,分布到多个 GPU 计算。
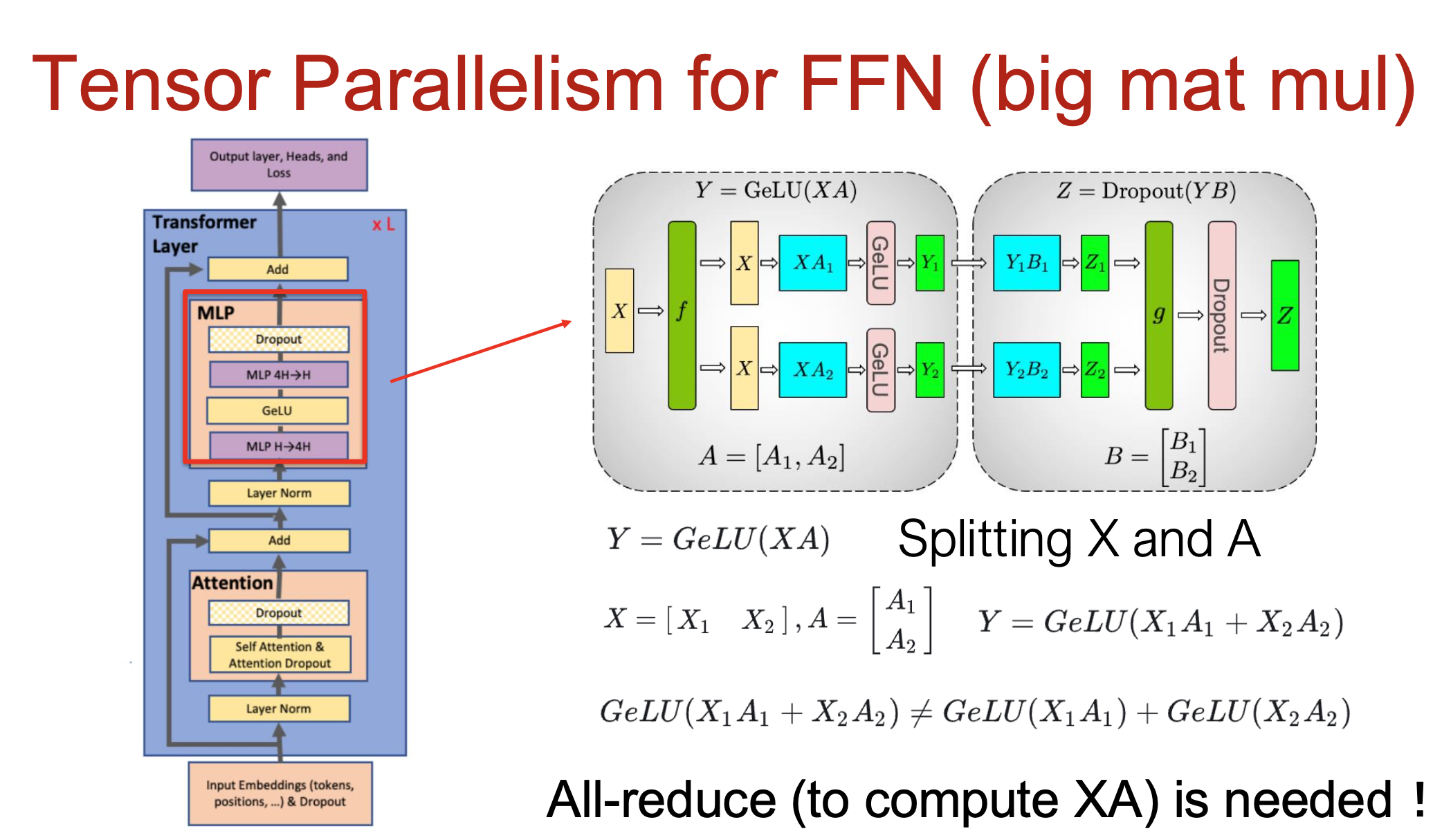
- TP 关注模型中 大矩阵乘法 的拆分 (例如FFN)
-
某些操作(如 LayerNorm、Dropout、Residual)不宜拆分,因通信开销过高
-
TP 主要关注于拆分模型中最大的计算部分(如 FFN 中的大矩阵乘法)。然而,模型中还有一些操作,例如:层归一化 (Layer Norm) (Dropout)残差连接 (Residual Connections)
- 这些操作的计算量相对较小,且通常涉及输入张量的所有维度。如果尝试拆分它们,所需的通信开销(例如 All-gather 或 All-reduce)往往会超过节省的计算时间
在 TP 中,
- 每个 GPU 仅保存部分权重(如 $A_1, A_2, B_1, B_2$)。
- 各自计算对应梯度并独立更新。
- 不需要与其他 GPU 同步所有梯度(这与数据并行 DP 的做法不同)。
4 混合并行(Hybrid Parallelism)
4.1 PP + TP 混合(Model Parallel)
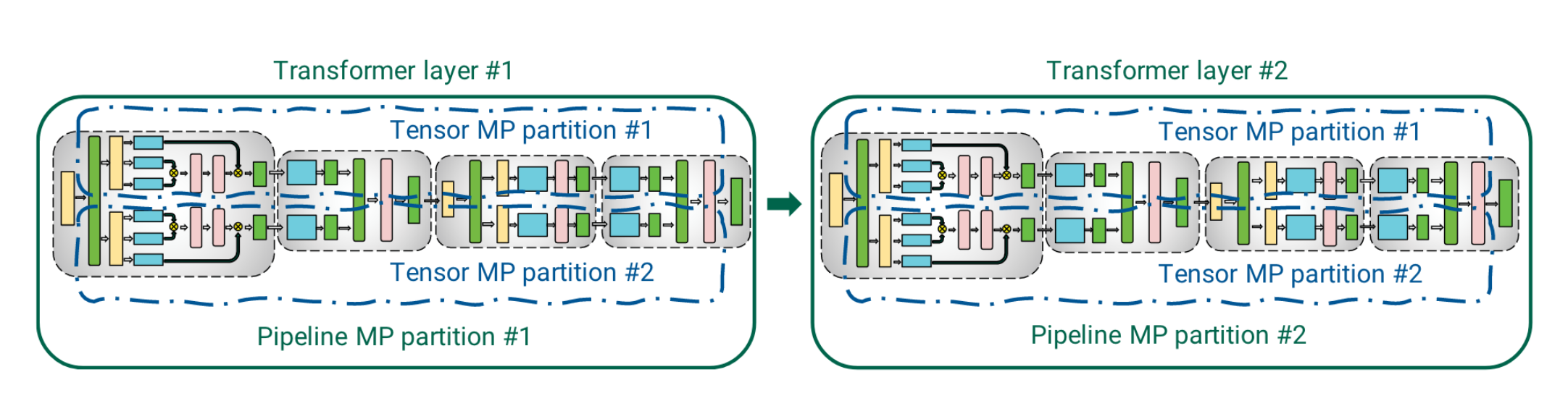
如图,先拆分PP,在PP里面拆TP
- 节点内优先 TP(利用 NVLink 加速通信)。
- 节点间采用 PP(激活值传输量小),通讯开销比较小,减少显存负担
节点内优先 TP,TP依赖nvlink通讯,加速计算
节点间用PP,通过传输少量激活值,通讯开销比较小,减少显存负担
4.2 DP + MP (DP + PP + TP)混合并行
- 先确定模型并行规模 \(M = tp_size \times pp_size\)
确保模型拆成M份后,不会超出单个GPU的内存
模型并行是一个节省显存的策略
- DP,扩展加速
一旦确定好 M, 剩余的GPU显存用于DP
数据并行的核心作用是缩短训练时间。它通过将整个批次拆分到不同的模型副本上并行计算, 而有效增加训练的 GPU 总数,提升吞吐量