LLM模型的量化策略

Low precision numbers in computer

1.1 LLM 的推理与训练成本

以典型大模型为例：

Llama-70B
- 训练成本：39.3M H100-80GB GPU hours
- 推理显存需求：≈140GB GPU memory
DeepSeek V3（671B 参数）
- 训练成本：2.8M H800 GPU hours
- 推理显存需求：>400GB GPU memory

大模型的训练与推理都极度依赖 GPU 计算与显存带宽，促使低精度计算成为主流优化方向。

1.2 模型量化（Model Quantization）

使用低 bit 精度（如 INT8、FP16、BF16）表示模型参数与中间层输出：

优点：
- 显著减少显存占用 → 可使用更大 batch size；
- 提升计算效率，一次 cycle 计算更多数据；
缺点：
- 精度下降，累积量化误差可能影响模型性能。

1.3 数值精度格式（Precision Formats）

percision format

INT8： 范围 $[-128,127]$，整数精度；
BF16 / FP16： 浮点半精度，常用于混合精度训练。

参考：BFloat16 文档

2 BF16/FP16 加速原理与 CUDA 支持

2.1 HFMA2 半精度融合乘加指令

HFMA2 (Half-precision Fused Multiply-Add) 在 1 个 cycle 内完成 2 个融合乘加运算，实现约 2 倍吞吐加速

2.1.1 执行过程

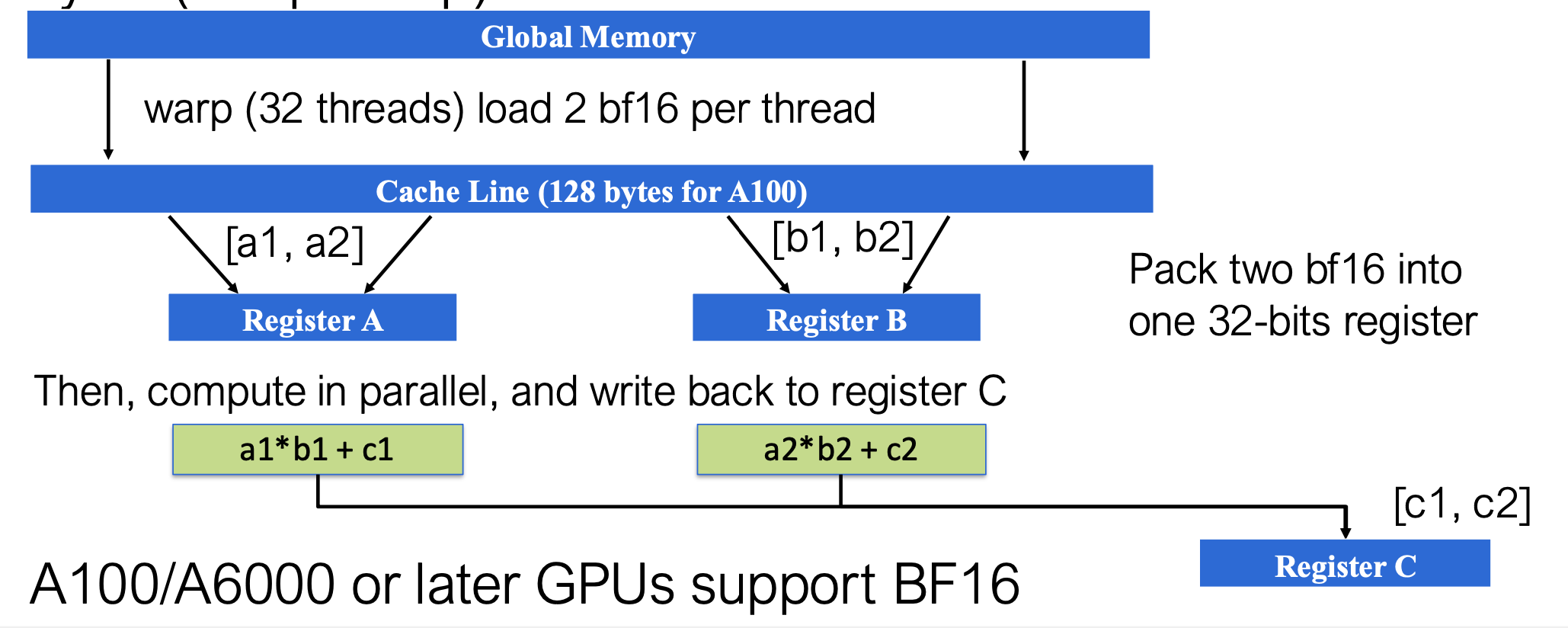
alt text

数据加载：从全局内存加载 BF16 数据（Warp=32 线程，每线程加载2个bf16数值）
数据打包：将两个 BF16 值打包到 32 位寄存器中
- Register A → [a₁, a₂]
- Register B → [b₁, b₂]
并行计算： $\begin{cases} c_1 = a_1 \times b_1 + c_1 \ c_2 = a_2 \times b_2 + c_2 \end{cases}$
结果存储：输出 [c₁, c₂] 写入 Register C

2.2 半精度 CUDA API 示例

2.2.1 向量加法（`__hadd2`）

__device__ __half2 __hadd2(const __half2 a, const __half2 b)

逐元素加法；
使用 RNE（Round-to-Nearest-Even） 舍入模式保证数值稳定性。

2.2.2 向量融合乘加（`__hfma2`）

__device__ __half2 __hfma2(const __half2 a, const __half2 b, const __half2 c)

执行 $a * b + c$ 的融合运算，同样使用 RNE 模式。

一条指令完成乘加；
每 cycle 处理 2 个元素；
吞吐率提升 2 倍。

3 基础量化方法（Basic Quantization Methods）

3.1 直接量化策略（Direct Quantization）

将 FP32 参数直接压缩为低精度格式（INT8/INT4）并在低精度下计算。

潜在问题：
- 精度损失与量化噪声；
- 数值范围不匹配（Range Mismatch）；
- 量化误差（Quantization Error）。

3.2 量化单个数值的方式

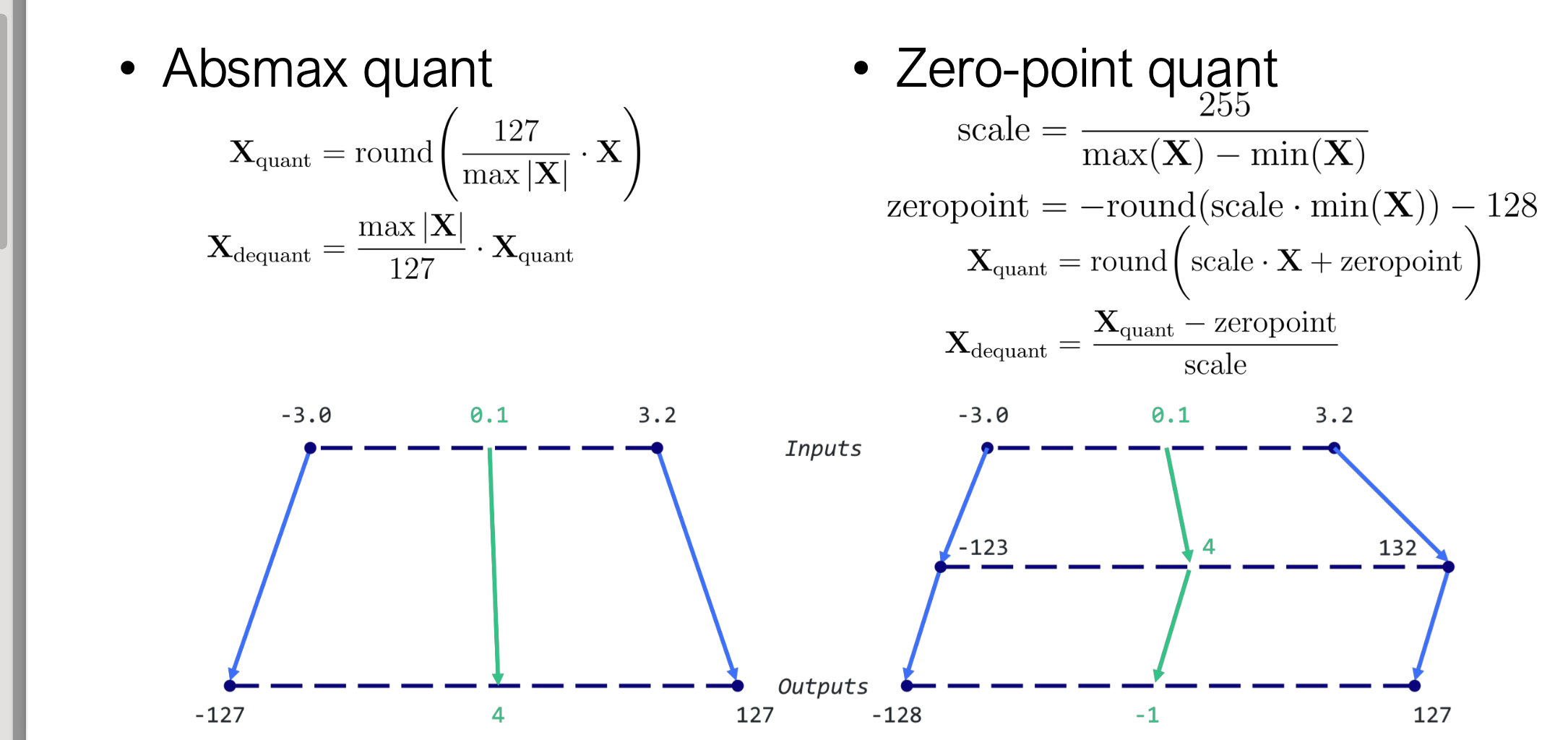
Absmax & Zero-point

3.2.1 Absmax 量化（对称量化）

计算最大绝对值： $\text{scale} = \frac{127}{\max|X|}$ 对称映射到 $[-127,127]$。

import torch
def absmax_quantize(X):
    # Calculate scale
    scale = 127 / torch.max(torch.abs(X))
    # Quantize
    X_quant = (scale * X).round()
    # Dequantize
    X_dequant = X_quant / scale
    return X_quant.to(torch.int8), X_dequant

3.2.2 Zero-Point 量化（非对称量化）

计算实际范围：

计算范围与零点： $\text{scale} = \frac{255}{\max(X)-\min(X)}, \quad \text{zeropoint} = (-\text{scale}\times\min(X)-128)$

零点计算：确定原始0值映射到的INT8位置

非对称映射：

输入范围：[-3.0, 3.2] 输出范围：[-128, 127]（256个值）充分利用所有256个离散值

其实就是通过零点加了个偏移量

def zeropoint_quantize(X):
    # Calculate value range (denominator)
    x_range = torch.max(X) - torch.min(X)
    x_range = 1 if x_range == 0 else x_range
    # Calculate scale
    scale = 255 / x_range
    # Shift by zero-point
    zeropoint = (-scale * torch.min(X) - 128).round()
    # Scale and round the inputs
    X_quant = torch.clip((X * scale + zeropoint).round(), -128,
    127)
    # Dequantize
    X_dequant = (X_quant - zeropoint) / scale
    return X_quant.to(torch.int8), X_dequant

参考：Google Colab 示例

4 逐层量化方法（Layer-wise Quantization）

4.1 AdaQuant

4.2 ZeroQuant

ZeroQuant

采用逐层蒸馏策略（Teacher 原模型 → Student 量化模型）；
精度优于简单 PTQ；
已集成于 DeepSpeed

4.3 LLM.int8()

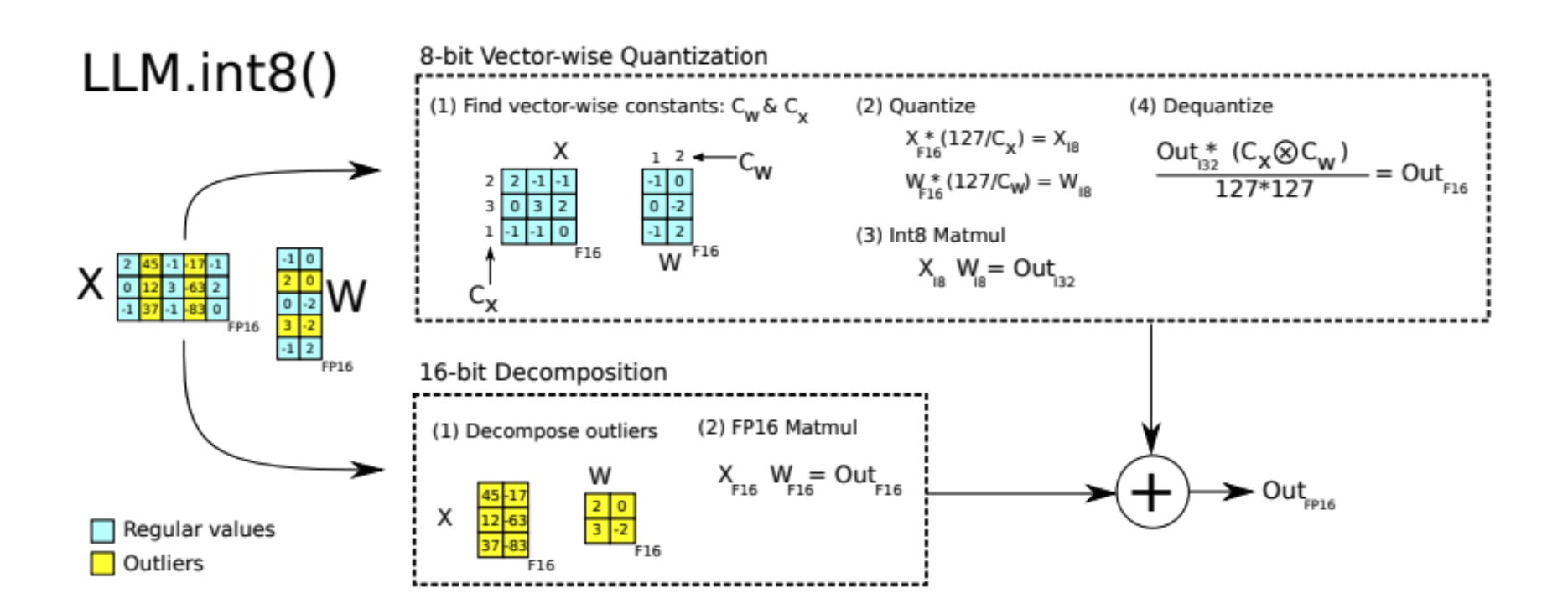
LLM.int8

对矩阵乘法部分使用 INT8；
解决激活值异常值（outliers）问题；
采用混合精度：异常值保持 FP16，正常值使用 INT8

异常值判断标准：

幅度 ≥ 6.0；
层级覆盖 ≥ 25%；
序列维度覆盖 ≥ 6%。

参考：LLM.int8(): 8-bit Matrix Multiplication for Transformers at Scale, NeurIPS 2022.

5 GPTQ 量化（Gradient-based Post-Training Quantization）

5.1 基本思想

Gradient-based Post-Training Quantization）是一种后训练量化（PTQ）

通过最小化量化误差，使量化后的权重输出尽可能接近原模型输出：

\[\min_{\hat{W}} | W X - \hat{W} X |_2^2\]

其中：

$ X $：输入数据到当前层（维度 $ d \times \text{Len} $）
$ W $：原始投影矩阵（projection matrix）
$ \hat{W} $：量化后的权重矩阵

即：找到一个量化后的矩阵 $ \hat{W} $，使得在输入数据 $ X $ 上，前向输出与原始 $ W $ 的结果尽可能接近。

5.2 核心思路

按列块量化（Column-wise Quantization）
- GPTQ 不是一次性量化整个权重矩阵，而是每次量化一个列块（column-block）。
- 这样可以逐步控制误差累积，使得每一步的量化决策更精细
误差补偿机制（Error Compensation）
- 当一个列块被量化后，GPTQ 会更新所有尚未量化的权重列。
- 更新的目的在于：compensate for the error incurred by quantizing a single weight
- 即：通过调整未量化的部分，补偿当前量化带来的误差，使整体的输出误差最小化

参考：GPTQ: Accurate Post-Training Quantization for Generative Pre-trained Transformers. Frantar et al. ICLR 2023.

5.3 算法步骤

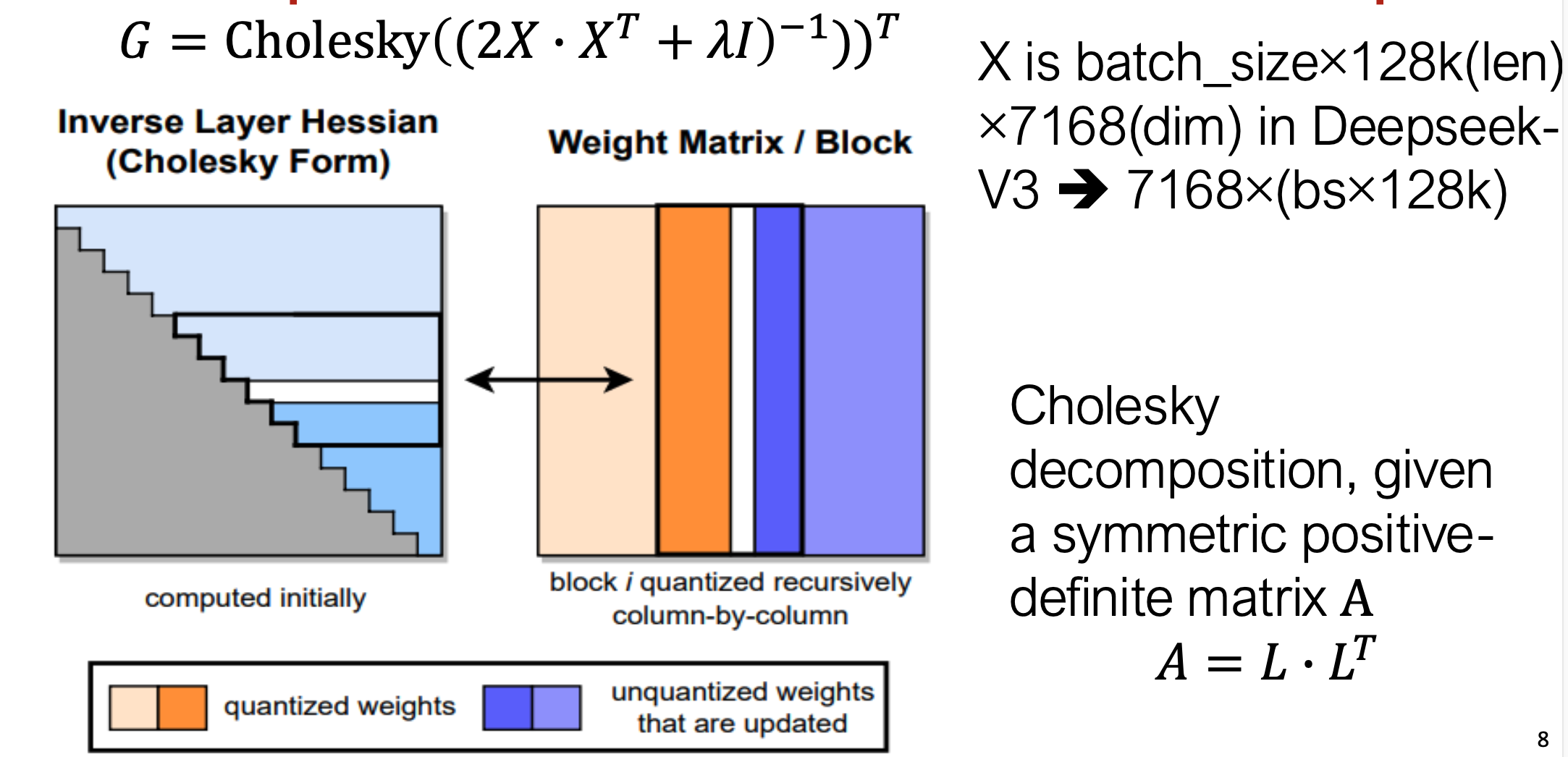
alt text

Hessian 逆矩阵 Cholesky 分解
- 对当前线性层（Linear Layer）的输入数据 $X$ ，计算其 Hessian 矩阵的逆矩阵并进行 Cholesky 分解，以便后续快速计算加权误差的更新
- 这一操作相当于建立输入的二阶统计量基础，用于后续的误差传播与补偿

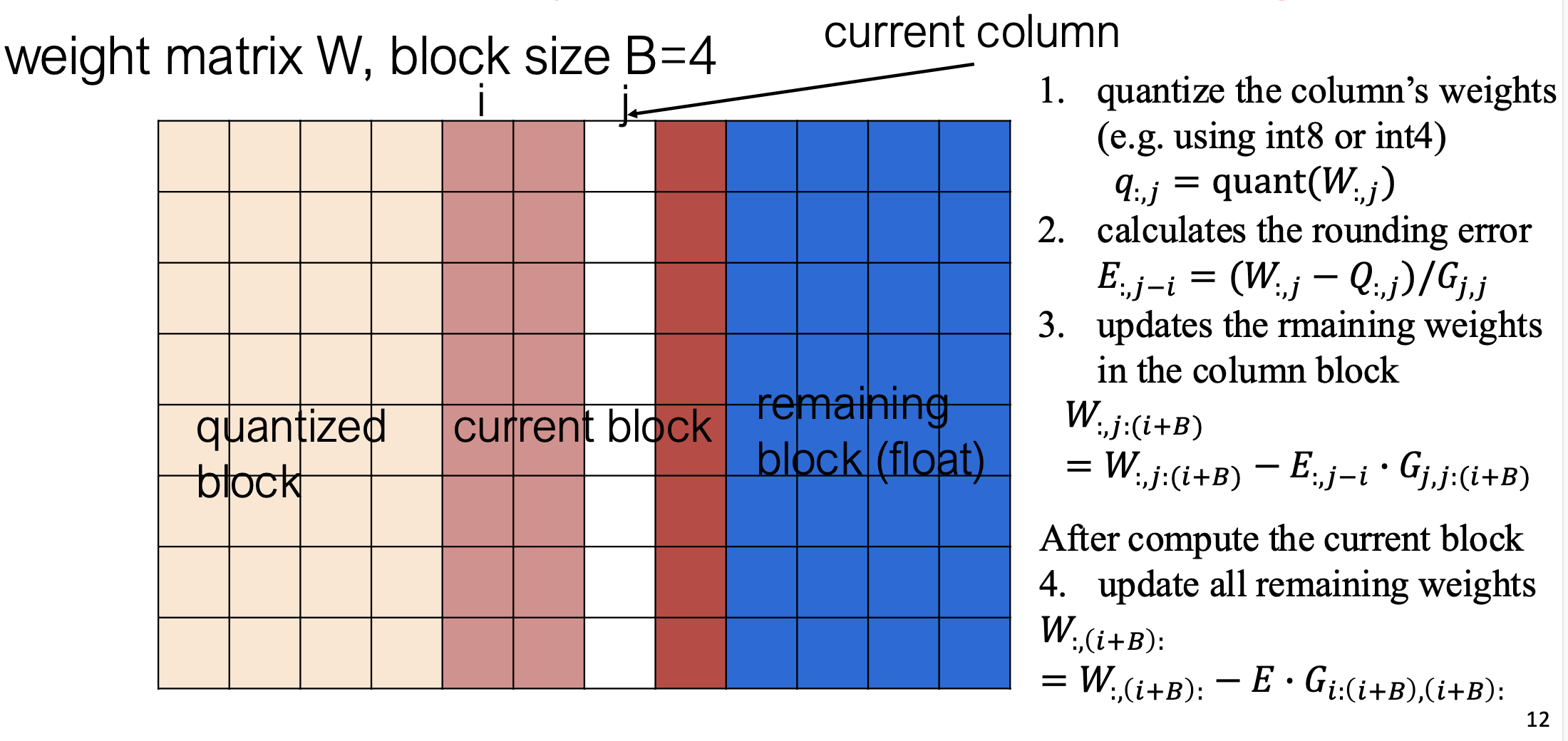
alt text

逐批（batch）处理权重矩阵 ( W ) 的列块（column block） 对每一批列块执行以下操作：
1. 权重量化（Quantization）
  - 使用某种“舍入（rounding）”方法（例如逐元素最邻近量化或最优舍入策略）将浮点权重转换为低比特整数。
2. 计算舍入误差（Rounding Error）
  - 计算量化前后的权重差值，以评估量化造成的误差大小。
3. 更新当前列块内的权重（Update Weights in Block）
  - 根据计算得到的舍入误差，对当前列块权重进行调整，使得在量化约束下误差最小化。
4. 更新未量化列的权重（Propagate Error to Remaining Weights）
  - 在当前列块处理完后，利用该块的误差信息，更新所有尚未量化的列块，从而在整个矩阵层面实现误差补偿。

伪代码：

alt text

6 GPTQ 与二阶优化理论（OBS / OBQ）

单权重量化可通过最优脑外科方法（Optimal Brain Surgeon, OBS）求解
- 当我们量化权重矩阵 ( W ) 中的一个权重时，这个问题可以被看作是一个 OBS（Optimal Brain Surgeon） 问题。
- OBS 理论表明，在已知 Hessian 矩阵的情况下，可以通过解析方式找到使误差最小化的单参数更新。
- 因此，在 GPTQ 中，我们可以一次更新一列（column）权重，使得量化误差最小。
高效更新逆 Hessian：利用秩-1 更新（rank-1 update）
- 在逐列量化的过程中，GPTQ 需要不断更新 Hessian 的逆矩阵。
- 这一过程可以通过 Optimal Brain Quantization (OBQ) 方法实现，即通过 rank-1 更新公式 来快速近似新的逆矩阵，而无需重新求逆。
- 实际实现中，GPTQ 使用 Cholesky 分解（Cholesky Decomposition） 预先计算出 Hessian 的分解形式，以进一步加速更新过程。
基于舍入误差的延迟批量更新（Batch and Lazy Update）
- 在每次计算舍入误差（rounding error）后，GPTQ 不会立即更新全部权重。
- 它采用一种“延迟（lazy）”的方式：批量计算并更新多个列块的误差补偿，从而在保持精度的同时提升效率。

6.1 Optimal Brain Surgeon (OBS)

基于二阶泰勒展开的最优单权重调整法：

\[\omega_p = \arg\min_{\omega_p} \frac{\omega_p^2}{[H^{-1}]_{pp}}\]

补偿更新： $\delta_p = -\frac{\omega_p}{[H^{-1}]*{pp}} H^{-1}*{:,p}$

复杂度高达 $O(d^4)$，GPTQ 通过近似优化解决。

6.2 Optimal Brain Quantization (OBQ)

alt text

对比项	OBS（剪枝）	OBQ（量化）
目标	移除权重	低比特量化
优化变量	$\omega_p$	$w_q$
更新方式	$\delta_p=-\frac{\omega_p}{[H^{-1}]{pp}}H^{-1}$	$\delta_F=-\frac{w_q - quant(w_q)}{[H_F^{-1}]{pp}}(H_F^{-1})$
结果	稀疏化	低比特化

6.3 列块更新策略（Column-wise Update）

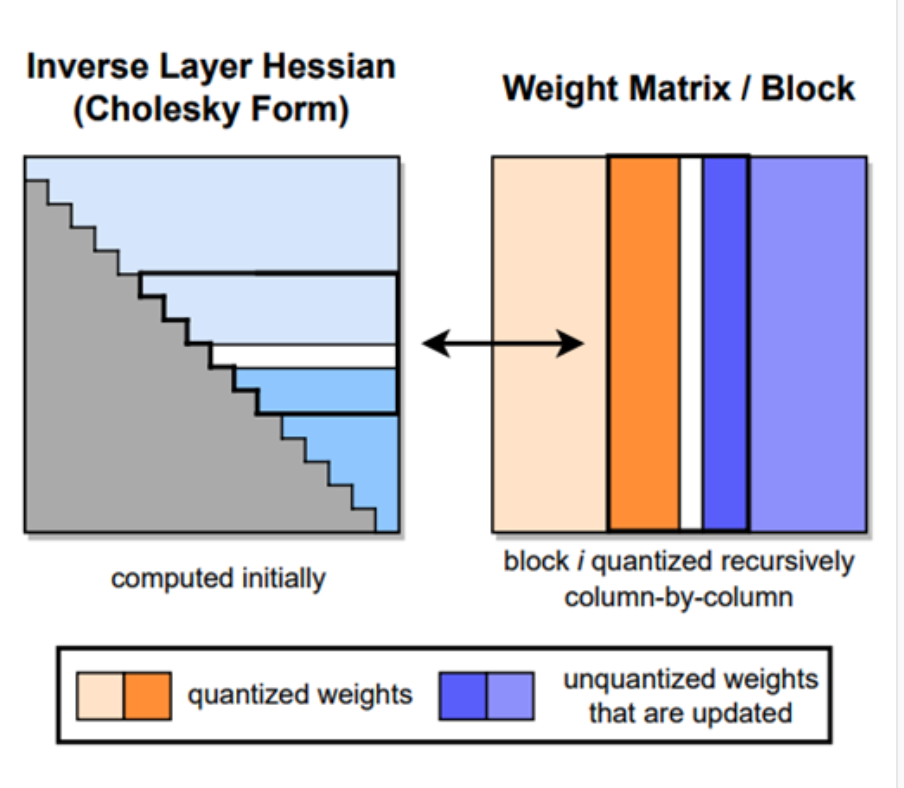
所有行共享同一逆 Hessian；
更新次数降为列数；
计算复杂度： $O(d_{row}\cdot d_{col}^3) ;\Rightarrow; O(\max(d_{row}\cdot d_{col}^2,, d_{col}^3))$

(a) 左图 — Inverse Layer Hessian (Cholesky Form)

表示层的逆 Hessian 矩阵经过 Cholesky 分解 存储；
每次量化一个列块（block）时，只需在分解矩阵中更新对应的下三角部分；
灰色区域：初始计算完成的部分；
蓝色区域：在逐列量化时动态更新的部分。

(b) 右图 — Weight Matrix / Block

表示当前正在量化的权重矩阵；
橙色块：已量化的列；
蓝色块：尚未量化、但被误差补偿更新的列；
每个 block 按列递归地被量化（从左到右）。

6.4 惰性批量更新（Lazy Batch Update）

6.4.1 问题背景：Naïve column update 太慢

逐列更新（naïve column update）的问题：

每量化完一列就立刻更新逆 Hessian 与权重矩阵；

这种操作需要频繁访问显存（memory access），而每次计算量较小；

因此会造成：

低计算/访存比（low compute-to-memory-access ratio）
GPU 计算单元利用率低（cannot highly utilize GPUs compute）

6.4.2 核心观察

GPTQ 的作者注意到：

列 i 的量化决策（rounding decision）只会受到该列自身更新的影响；不会受到未来（后面列）的更新影响。即：当前列的舍入误差与未来列无关。
后续列的更新（later columns updates）在当前时刻其实是无关紧要的（irrelevant），可以暂时不执行。因此可以先推迟（lazy）这些更新，一次性在后续批量完成。

6.4.3 解决方案懒批量更新

为提高效率，GPTQ 不在每列量化后立即更新所有相关列，而是：

将若干列合并成一个 batch（列块）

在处理完该批次后，再一次性执行更新操作

数学表达为： $[ W_{:,(i+B)} = W_{:,(i+B)} - E \cdot G_{i:(i+B),(i+B)} ]$ 其中：

( W_{:,(i+B)} )：后续未量化列的权重；
( E )：量化误差矩阵；
( G )：Hessian 逆矩阵相关项；
( i:(i+B) )：表示该批量内的列范围。

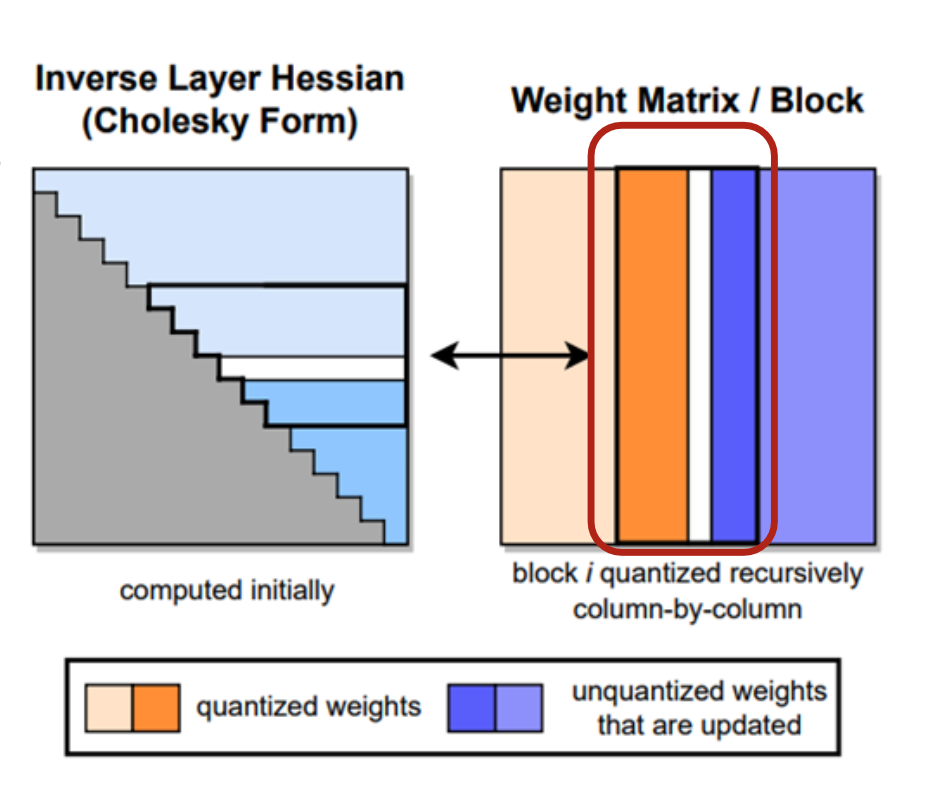
alt text

(a) 左图 — Inverse Layer Hessian (Cholesky Form)

灰色：初始计算完成；

蓝色：在量化时逐步更新；

表示 Hessian 的 Cholesky 结构，量化时只需访问部分子矩阵。

(b) 右图 — Weight Matrix / Block

橙色列：已量化的列；

蓝色列：尚未量化但被更新影响的列；

红色框：表示当前处理的“列块（batch of columns）”；

每次量化多个列（batch）后，才进行一次统一的权重更新

优点：

减少访存；
提高计算/访存比；
GPU 利用率显著提升。

7 数值稳定性与 Cholesky 优化

7.1 数值问题（Numerical inaccuracies）

在大规模 LLM 的量化过程中，一个严重的问题是：

当层的 Hessian 维度极大时，其逆矩阵 ( H_F^{-1} ) 容易变得不稳定（indefinite）；
即矩阵可能不再是正定的，从而导致量化更新过程中产生数值误差累积或数值溢出；
这会严重影响量化后的模型性能

7.2 关键观察（Observation）

在量化过程中，其实只需要从 ( H_F^{-1} ) 中提取非常有限的信息：

当量化某个权重 ( q ) 时，仅需访问 ( H_F^{-1} ) 第 ( q ) 行（从对角线开始的部分）即可。

也就是说：

不需要完整存储或反复求逆整个 ( H_F^{-1} )；
只需使用下三角部分（Lower-triangular）即可完成所有更新操作。

7.3 GPTQ 的优化策略

GPTQ 利用了 Cholesky 分解（Cholesky decomposition） 的数学特性： $H = L L^{T} \quad \Rightarrow \quad H^{-1} = (L^{-1})^{T} L^{-1}$ GPTQ 在实现中：

使用 Cholesky 核函数（Cholesky kernels） 预先计算 ( H^{-1} ) 所需的信息；
将 Hessian 的逆运算转换为下三角矩阵分解与前向求解；
这样既能保持数值稳定，又不会显著增加显存消耗。

7.4 图示解读

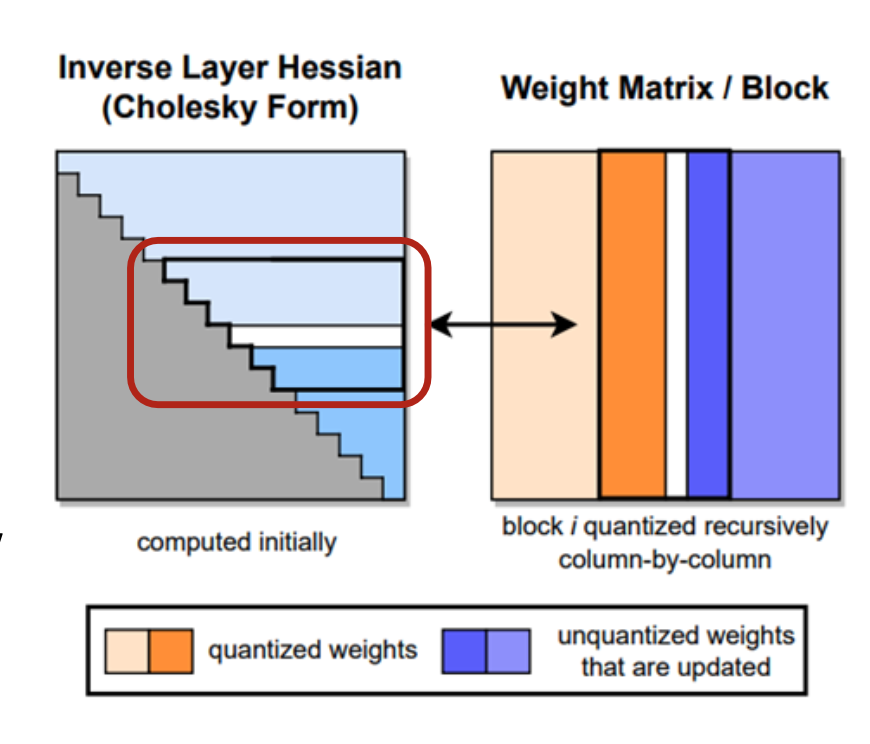
alt text

左图（Inverse Layer Hessian / Cholesky Form）
- 灰色区域：初始计算完成的部分；
- 蓝色区域：在量化时动态访问；
- 红框：表示 Cholesky 分解中被访问的下三角子块。
右图（Weight Matrix / Block）
- 橙色：已量化权重；
- 蓝色：未量化但需要更新的权重列。
- 表示在逐列量化过程中，Cholesky 形式的 ( H_F^{-1} ) 提供稳定的误差补偿支撑。

8 GPTQ 代码实现

官方实现仓库： https://github.com/qwopqwop200/GPTQ-for-LLaMa
核心实现文件： gptq.py

上篇分布式模型并行

下篇高效参数微调

Low precision numbers in computer

1.1 LLM 的推理与训练成本

1.2 模型量化（Model Quantization）

1.3 数值精度格式（Precision Formats）

2 BF16/FP16 加速原理与 CUDA 支持

2.1 HFMA2 半精度融合乘加指令

2.1.1 执行过程

2.2 半精度 CUDA API 示例

2.2.1 向量加法（__hadd2）

2.2.2 向量融合乘加（__hfma2）

3 基础量化方法（Basic Quantization Methods）

3.1 直接量化策略（Direct Quantization）

3.2 量化单个数值的方式

3.2.1 Absmax 量化（对称量化）

3.2.1 Absmax 量化（对称量化）

3.2.2 Zero-Point 量化（非对称量化）

4 逐层量化方法（Layer-wise Quantization）

4.1 AdaQuant

4.2 ZeroQuant

4.3 LLM.int8()

5 GPTQ 量化（Gradient-based Post-Training Quantization）

5.1 基本思想

5.2 核心思路

5.3 算法步骤

6 GPTQ 与二阶优化理论（OBS / OBQ）

6.1 Optimal Brain Surgeon (OBS)

6.2 Optimal Brain Quantization (OBQ)

6.3 列块更新策略（Column-wise Update）

(a) 左图 — Inverse Layer Hessian (Cholesky Form)

(b) 右图 — Weight Matrix / Block

6.4 惰性批量更新（Lazy Batch Update）

6.4.1 问题背景：Naïve column update 太慢

6.4.2 核心观察

6.4.3 解决方案 懒批量更新

(a) 左图 — Inverse Layer Hessian (Cholesky Form)

(b) 右图 — Weight Matrix / Block

7 数值稳定性与 Cholesky 优化

7.1 数值问题（Numerical inaccuracies）

7.2 关键观察（Observation）

7.3 GPTQ 的优化策略

7.4 图示解读

8 GPTQ 代码实现

2.2.1 向量加法（`__hadd2`）

2.2.2 向量融合乘加（`__hfma2`）

6.4.3 解决方案懒批量更新