1 LayerNorm(层归一化)
1.1 提出背景
LayerNorm 是 Transformer(Vaswani et al., 2017)原始论文中使用的标准归一化方法
1.2 数学定义
\(y = \frac{x - \mathbb{E}[x]}{\sqrt{\mathrm{Var}[x]} + \epsilon} \times \gamma + \beta\)
其中:
- 对输入 $x \in \mathbb{R}^{d_{model}}$ 的每个样本(token 向量)进行归一化;
- 减去均值 $\mathbb{E}[x]$;
- 除以标准差 $\sqrt{\mathrm{Var}[x]}$;
- 然后再加上可学习的缩放参数 $\gamma$ 和偏置 $\beta$
1.3 作用与目标
让每个 token 的特征在不同维度上具有相似的分布(零均值、单位方差), 以防止训练初期层间激活值过大或过小
1.4 应用代表模型
GPT-1 / GPT-2 / GPT-3, OPT, GPT-J, BLOOM 均沿用标准 LayerNorm 结构
2 RMSNorm(Root Mean Square Normalization)
2.1 提出背景
随着模型规模扩大,LayerNorm 的计算开销(特别是均值减法)和数值稳定性问题被放大。 RMSNorm(Zhang & Sennrich, 2019)作为简化版被引入大模型训练中。
2.2 数学定义
\(y = \frac{x}{\sqrt{\frac{1}{d}|x|_2^2 + \epsilon}} \times \gamma\)
2.3 与 LayerNorm 的区别
| 特征 | LayerNorm | RMSNorm |
|---|---|---|
| 是否减均值 | 减去 $\mathbb{E}[x]$ | 不减 |
| 是否加偏置 β | 有 | 无 |
| 归一化依据 | 方差 Var[x] | 均方根 RMS(x) |
| 可学习参数 | γ、β | 仅 γ |
| 稳定性 | 好 | 更快、更简单 |
| 计算量 | 稍大(含减均值) | 更小 |
2.4 直观理解
- LayerNorm = “标准化后居中”
- RMSNorm = “仅缩放,不居中”
RMSNorm 只依赖向量的平方和($||x||^2$),因此更稳定、更高效。 在分布非常大的模型中,这种简化减少了不必要的浮点误差传播
2.5 应用代表模型
LLaMA 系列、PaLM、Chinchilla、T5 均采用 RMSNorm 或其 Pre-Norm 变体。
3 为什么现代 LLM 更倾向 RMSNorm
3.1 更高的数值稳定性
- 在超深网络中,LayerNorm 的均值项可能引入数值波动;
- RMSNorm 避免了减均值操作,使梯度传播更稳定。
3.2 更低的计算代价
- 少一次 mean 计算与 bias 加法;
- 特别在 Transformer 的每个层都归一化时,累计可节省 1~2% 的 FLOPs (看似不多,但是后面还要讲)
3.3 与 Pre-Norm 结构的结合
- RMSNorm 常放在每个子层输入端(Pre-Norm),直接调整幅值;
- 不需要“重新居中”,避免破坏残差的均值结构(避免残差漂移)
4 Infra 层面上 RMSNorm 与 LayerNorm的 对比
4.1 LayerNorm 的通信特征
LayerNorm 计算: \(y = \frac{x - \mathbb{E}[x]}{\sqrt{\mathrm{Var}[x]} + \epsilon} \times \gamma + \beta\) 需要两次统计:
- 均值 $\mathbb{E}[x]$
- 方差 $\mathrm{Var}[x] = \mathbb{E}[x^2] - (\mathbb{E}[x])^2$
在分布式训练中(如 tensor parallel),每个 GPU 持有部分 hidden 维度(例如 $8192 / 8 = 1024$), 因此计算全局统计时需:
两次 AllReduce(均值 + 平方均值)
代价包括通信延迟、同步依赖和 overlap 难度增加
4.2 RMSNorm 的计算特性
RMSNorm 仅需计算: \(|x|_2^2 = \sum_i x_i^2\)
- 只做一次平方求和;
- 无需均值计算;
- 不含偏置项 β;
- 仅一次 reduce 操作
4.3 通信复杂度对比
| 操作 | LayerNorm | RMSNorm |
|---|---|---|
| 统计量 | mean + var | sum(x²) |
| AllReduce 次数 | 2 | 1 |
| 同步依赖 | 强 | 弱 |
| 通信占比 | 高 | 低 |
→ RMSNorm 拥有 更少的同步点、更高的 overlap 潜力,通信抖动更小。
从 infra(系统实现层面) 的角度来看, RMSNorm 相比 LayerNorm 确实减少了一次全局求均值(mean reduction)操作, 这直接带来了 通信开销更小、延迟更可控 的好处,尤其在 分布式并行训练(如 pipeline parallel、sequence parallel)场景下。
5 Infra 性能指标对比
5.1 FLOPs 占比分析
| Operator 类别 | % FLOPs | % Runtime |
|---|---|---|
| 矩阵乘(Tensor contraction) | 99.8% | 61.0% |
| 归一化(Stat. normalization) | 0.17% | 25.5% |
| 逐元素操作(Element-wise) | 0.03% | 13.5% |
矩阵乘法计算量最大但效率高; LayerNorm/RMSNorm FLOPs 极低但耗时高,因频繁读写内存与通信
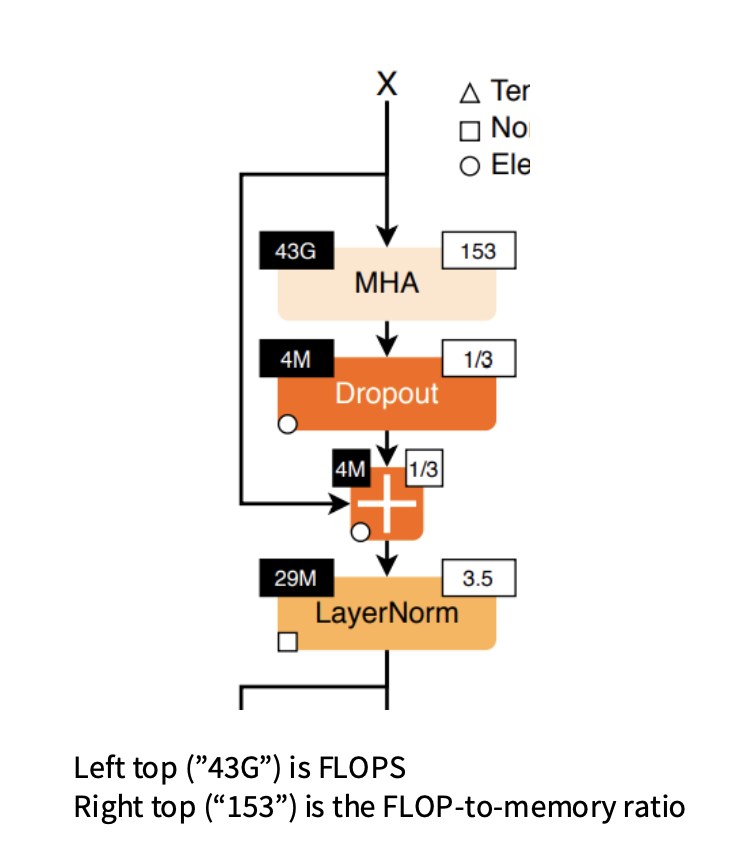
5.2 FLOP-to-Memory Ratio 分析
FLOP-to-memory ratio(计算密度) 表示“每访问 1 单位内存,可以执行多少次计算”
数字越大说明越算密集、GPU 效率越高。
MHA 的比值高(153)→ 计算密集型(算快,IO 比低)
LayerNorm/Dropout/Add 的比值极低(1/3~3.5)→ 内存密集型,花大量时间在读写数据
| 模块 | FLOPs | 比值 | 含义 |
|---|---|---|---|
| MHA(多头注意力) | 43G | 153 | 计算密集 |
| Dropout | 4M | 1/3 | 内存密集 |
| Add (+) | 4M | 1/3 | 内存密集 |
| LayerNorm | 29M | 3.5 | 内存密集型 |
计算密度低 → 带宽压力大 → IO 成为瓶颈。
5.3 Infra层面的总结
虽然 RMSNorm 在 FLOPs 上收益极小(仅 0.2%), 但从系统视角,或者叫 数据移动(Data Movement)
- 减少一次全局归约 → 减少通信与同步
- 减少内存访问 → 提升带宽利用率
- 无偏置项 β → 降低显存占用
- Kernel 更易与矩阵乘重叠执行
因此在大模型(在深层网络中累积效应明显)中,RMSNorm 的优势主要体现在 通信效率与数值稳定性 上
而且没有 bias, 省显存